1.3.1.导数在研究函数中的应用——单调性
文档属性
| 名称 | 1.3.1.导数在研究函数中的应用——单调性 |
|
|
| 格式 | rar | ||
| 文件大小 | 907.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-28 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
1.3 导数在研究函数中的应用
3.1.函数的单调性
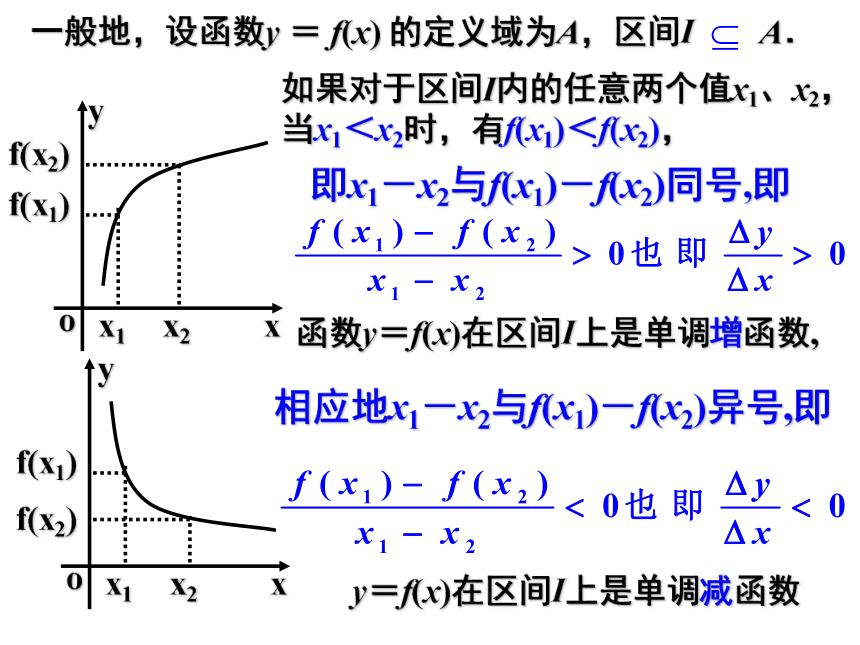
引例1.确定函数f(x)=x2-4x+3在哪个区间内是增函数 哪个区间内是减函数
在(-∞,2)上是减函数;
在(2,+∞)上是增函数。
2
y
x
0
解:f(x)=(x-2)2-1
问题情境
引例2.确定函数f(x)=2x3-6x2+7在哪个区间内是增函数 哪个区间内是减函数
问题情境
用定义法判断函数单调性的步骤:
(1)在给定的区间内任取x1( 2 ) 作差f(x1)-f(x2)并变形;
(3)判断符号;
(4)下结论。
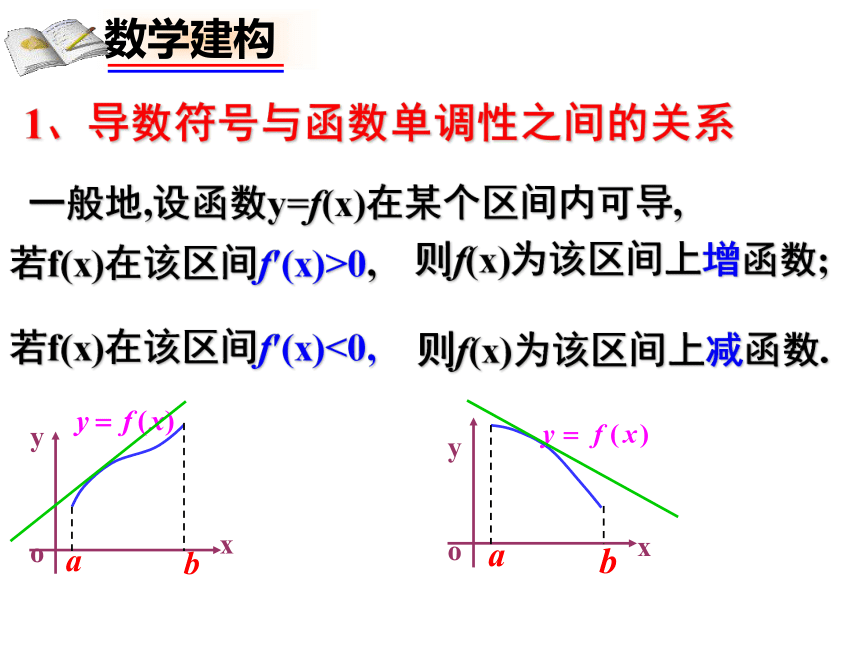
一般地,设函数y = f(x) 的定义域为A,区间I A.
如果对于区间I内的任意两个值x1、x2,当x1<x2时,有f(x1)<f(x2),
y=f(x)在区间I上是单调减函数
y
x
o
x1
x2
f(x1)
f(x2)
y
x
o
x1
x2
f(x1)
f(x2)
即x1-x2与f(x1)-f(x2)同号,即
相应地x1-x2与f(x1)-f(x2)异号,即
函数y=f(x)在区间I上是单调增函数,
一般地,设函数y=f(x)在某个区间内可导,
若f(x)在该区间f′(x)>0,
则f(x)为该区间上增函数;
则f(x)为该区间上减函数.
若f(x)在该区间f′(x)<0,
数学建构
1、导数符号与函数单调性之间的关系
x
y
o
x
y
o
学生活动
注1:如果在某个区间内恒有f′(x)=0,则f(x)为常数函数,不具有单调性.
思考1:若在某个区间内恒有f′(x)=0呢?
结合函数y=x3思考:如果f(x)在某区间上单调递增,那么在该区间上必有f′(x)>0吗?
x
y
o
y=x3
学生活动
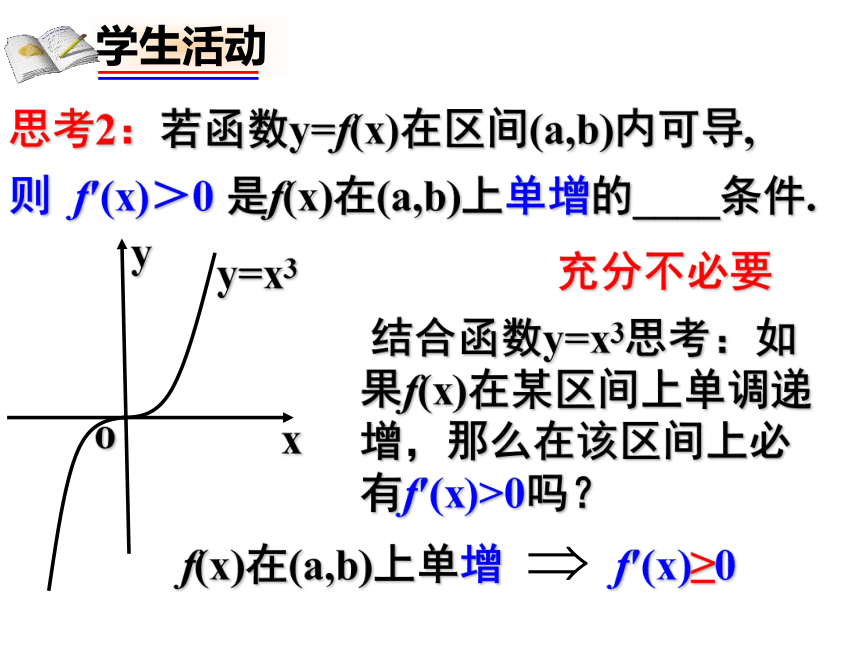
思考2:若函数y=f(x)在区间(a,b)内可导,
则 f′(x)>0 是f(x)在(a,b)上单增的____条件.
充分不必要
f′(x)≥0
f(x)在(a,b)上单增
例1.确定函数f(x)=2x3-6x2+7在哪些区间内是增函数?
数学应用
函数f(x)=2x3-6x2+7在区间 (-∞,0) 上是增函数,在区间 (2,+∞) 也上是增函数
变题1:求函数f(x)=2x3-6x2+7的单调区间.
变题2:求函数f(x)=2x3-6x2+7 ,x∈(-1,3)的单调增区间.
点评:利用导数求函数单调区间的步骤:
(2)求导数 ;
(3)解不等式组 得f(x)的单调递增区间;
解不等式组 得f(x)的单调递减区间.
(1)求y=f(x)的定义域D;
(4)下结论。
注意点:①单调区间是定义域的子集;
②多个单调区间不能并起来。
练习1:求函数f(x)=x-lnx 的单调增区间.
练习2:求函数 的单调增区间.
x
y
o
y=x
例2.证明函数f(x)=x-ln(x+1)在区间(1,+∞)上为单调递增函数.
数学应用
变题:证明不等式x>ln(x+1) (x>1)
(1)求导数 ;
(2)判断导函数在指定区间上符号的正负;
(3)下结论。
点评:利用导数证明函数单调性的步骤:
数学应用
例3:讨论函数f(x)=x3-3ax2-1(a≠0)的单调性。
变式:若函数f(x)=x3+ax2+6x-10在R上单调递增,求实数a的取值范围。
设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
2
(A)
(B)
(C)
(D)
数学应用
2.(1)函数f(x)=x2(2-x)的单调增区间是____;
(2)函数 的单调递减区间是_______.
1. 已知函数y=f(x)在定义域[-4,6] 内可导,其图象如图,记y=f(x)的导函数为f'(x),则不等式f'(x)≥0的解集为____________.
学生活动
通过这节课的学习你有哪些收获?
回顾反思
一个知识:
导数符号与函数单调性的关系:
二种题型:
①求函数的单调区间;
②证明不等式。
三个数学思想:
特殊到一般、数形结合、化归与转化
1.3 导数在研究函数中的应用
3.1.函数的单调性
引例1.确定函数f(x)=x2-4x+3在哪个区间内是增函数 哪个区间内是减函数
在(-∞,2)上是减函数;
在(2,+∞)上是增函数。
2
y
x
0
解:f(x)=(x-2)2-1
问题情境
引例2.确定函数f(x)=2x3-6x2+7在哪个区间内是增函数 哪个区间内是减函数
问题情境
用定义法判断函数单调性的步骤:
(1)在给定的区间内任取x1
(3)判断符号;
(4)下结论。
一般地,设函数y = f(x) 的定义域为A,区间I A.
如果对于区间I内的任意两个值x1、x2,当x1<x2时,有f(x1)<f(x2),
y=f(x)在区间I上是单调减函数
y
x
o
x1
x2
f(x1)
f(x2)
y
x
o
x1
x2
f(x1)
f(x2)
即x1-x2与f(x1)-f(x2)同号,即
相应地x1-x2与f(x1)-f(x2)异号,即
函数y=f(x)在区间I上是单调增函数,
一般地,设函数y=f(x)在某个区间内可导,
若f(x)在该区间f′(x)>0,
则f(x)为该区间上增函数;
则f(x)为该区间上减函数.
若f(x)在该区间f′(x)<0,
数学建构
1、导数符号与函数单调性之间的关系
x
y
o
x
y
o
学生活动
注1:如果在某个区间内恒有f′(x)=0,则f(x)为常数函数,不具有单调性.
思考1:若在某个区间内恒有f′(x)=0呢?
结合函数y=x3思考:如果f(x)在某区间上单调递增,那么在该区间上必有f′(x)>0吗?
x
y
o
y=x3
学生活动
思考2:若函数y=f(x)在区间(a,b)内可导,
则 f′(x)>0 是f(x)在(a,b)上单增的____条件.
充分不必要
f′(x)≥0
f(x)在(a,b)上单增
例1.确定函数f(x)=2x3-6x2+7在哪些区间内是增函数?
数学应用
函数f(x)=2x3-6x2+7在区间 (-∞,0) 上是增函数,在区间 (2,+∞) 也上是增函数
变题1:求函数f(x)=2x3-6x2+7的单调区间.
变题2:求函数f(x)=2x3-6x2+7 ,x∈(-1,3)的单调增区间.
点评:利用导数求函数单调区间的步骤:
(2)求导数 ;
(3)解不等式组 得f(x)的单调递增区间;
解不等式组 得f(x)的单调递减区间.
(1)求y=f(x)的定义域D;
(4)下结论。
注意点:①单调区间是定义域的子集;
②多个单调区间不能并起来。
练习1:求函数f(x)=x-lnx 的单调增区间.
练习2:求函数 的单调增区间.
x
y
o
y=x
例2.证明函数f(x)=x-ln(x+1)在区间(1,+∞)上为单调递增函数.
数学应用
变题:证明不等式x>ln(x+1) (x>1)
(1)求导数 ;
(2)判断导函数在指定区间上符号的正负;
(3)下结论。
点评:利用导数证明函数单调性的步骤:
数学应用
例3:讨论函数f(x)=x3-3ax2-1(a≠0)的单调性。
变式:若函数f(x)=x3+ax2+6x-10在R上单调递增,求实数a的取值范围。
设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
2
(A)
(B)
(C)
(D)
数学应用
2.(1)函数f(x)=x2(2-x)的单调增区间是____;
(2)函数 的单调递减区间是_______.
1. 已知函数y=f(x)在定义域[-4,6] 内可导,其图象如图,记y=f(x)的导函数为f'(x),则不等式f'(x)≥0的解集为____________.
学生活动
通过这节课的学习你有哪些收获?
回顾反思
一个知识:
导数符号与函数单调性的关系:
二种题型:
①求函数的单调区间;
②证明不等式。
三个数学思想:
特殊到一般、数形结合、化归与转化
