83.导数在实际生活中的应用
图片预览




文档简介
(共11张PPT)
2.函数f(x)=sin2x-x在
上的最大值为___;最小值为____.
5.使内接椭圆 =1的矩形面积最大,矩形的长为_____,宽为_____.
作业讲评
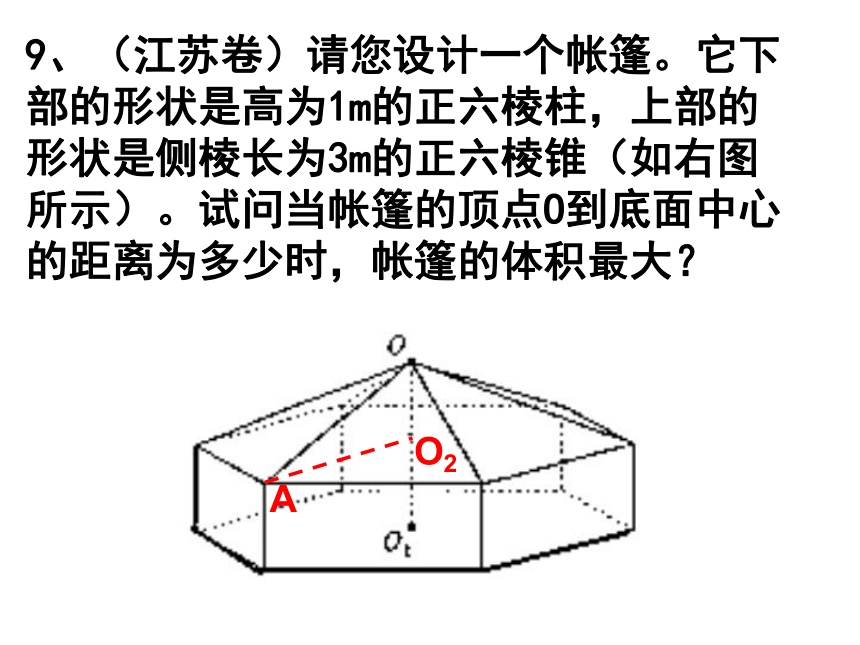
9、(江苏卷)请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心的距离为多少时,帐篷的体积最大?
A
O2
9、设OO2=x
令P′(x)=0,x=-3(舍)或x=1
当00,
当X>1时,V′(x)<0
当x=1时,V(x)为极大值,且为最大值。
已知函数f(x)=ax3+bx2+cx在x0处取得极大值5 ,其导函数y=f '(x)的图象经过点(1,0), (2,0), 如图, 求: (1)x0及函数f(x)解析式;
(2)设g(x)=f(x)+m, 若对于 x [0,2]不等式g(x)变1.讨论方程f(x)=k的实根个数;
变2.若函数y=f(x)在[m,n]上的值域为 [4,9],求m,n满足的条件;
83. 导数在
实际生活中的应用
一.用导数解决实际问题的步骤:
读 题(文字语言)
建 模(数学语言)
导数求解(数学应用)
反 馈 (检验作答)
二.建立模型的步骤 (建立目标函数):
(1)根据题意找出与问题有关的各个量,分清其中哪些是变量,哪些是常量.
(2)确定变量中的哪个量作为因变量,通常是取要求最值的那个变量作为因变量,而自变量一般有多种取法,自变量选取是否得当,与解题难易关系密切,务必格外注意.
(3)利用问题的条件,结合平面几何.解析几何及物理中有关力学,电学,光学等方面的知识,找出变量之间的依存关系,同时确定自变量的取值范围,这样便可得到目标函数.
例1.在如图所示的电路中,已知电源的内阻为r,电动势为E,外电阻R为多大时,才能使电功率最大?最大电功率是多少?
分析:
例2.强度分别为a,b的两个光源A,B,他们间的距离为d,试问:在连接这两个光源的线段AB上,何处照度最小?试就a=8,b=1,d=3时回答上述问题(照度与光的强度成正比,与光源距离的平方成反比)
A
B
P
a=8
b=1
x
3-x
分析:
例3、在经济学中,生产x单位产品的成本
称为成本函数,记为C(x);出售x单位产品
的收益称为收益函数,记为R(x);
R(x)-C(x)称为利润函数,记为P(x).
(1)设C(x)=10-6x3-0.003x2+5x+1000,
生产多少单位产品时,边际成本C′(X)最低?
(2)设C(x)=50x+10000,产品的单价
p=100-0.01x,怎样定价,可使利润最大?
阅读P 15 : 链接---边际函数
有一隧道既是交通拥挤地段,又是事故多发地段.为了保证安全,交通部门规定,隧道内的车距d(m)正比于车速v(km/h)的平方与自身长L(m)的积,且车距不得小于半个车身长,而当车速为60(km/h)时,车距为1.44个车身长.在交通繁忙时,应规定怎样的车速,可以使隧道的车流量最大?
课堂练习:
P38/4
生产某塑料管的利润函数为P(n)=-n3+600n2+67500n-1200000,其中n为工厂每月生产该塑料管的根数,利润P(n)的单位为元.
(1)求边际利润函数P′(n);
(2)求使P′(n)=0的值;
(3)解释(2)中的n值的实际意义.
2.函数f(x)=sin2x-x在
上的最大值为___;最小值为____.
5.使内接椭圆 =1的矩形面积最大,矩形的长为_____,宽为_____.
作业讲评
9、(江苏卷)请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心的距离为多少时,帐篷的体积最大?
A
O2
9、设OO2=x
令P′(x)=0,x=-3(舍)或x=1
当0
当X>1时,V′(x)<0
当x=1时,V(x)为极大值,且为最大值。
已知函数f(x)=ax3+bx2+cx在x0处取得极大值5 ,其导函数y=f '(x)的图象经过点(1,0), (2,0), 如图, 求: (1)x0及函数f(x)解析式;
(2)设g(x)=f(x)+m, 若对于 x [0,2]不等式g(x)
变2.若函数y=f(x)在[m,n]上的值域为 [4,9],求m,n满足的条件;
83. 导数在
实际生活中的应用
一.用导数解决实际问题的步骤:
读 题(文字语言)
建 模(数学语言)
导数求解(数学应用)
反 馈 (检验作答)
二.建立模型的步骤 (建立目标函数):
(1)根据题意找出与问题有关的各个量,分清其中哪些是变量,哪些是常量.
(2)确定变量中的哪个量作为因变量,通常是取要求最值的那个变量作为因变量,而自变量一般有多种取法,自变量选取是否得当,与解题难易关系密切,务必格外注意.
(3)利用问题的条件,结合平面几何.解析几何及物理中有关力学,电学,光学等方面的知识,找出变量之间的依存关系,同时确定自变量的取值范围,这样便可得到目标函数.
例1.在如图所示的电路中,已知电源的内阻为r,电动势为E,外电阻R为多大时,才能使电功率最大?最大电功率是多少?
分析:
例2.强度分别为a,b的两个光源A,B,他们间的距离为d,试问:在连接这两个光源的线段AB上,何处照度最小?试就a=8,b=1,d=3时回答上述问题(照度与光的强度成正比,与光源距离的平方成反比)
A
B
P
a=8
b=1
x
3-x
分析:
例3、在经济学中,生产x单位产品的成本
称为成本函数,记为C(x);出售x单位产品
的收益称为收益函数,记为R(x);
R(x)-C(x)称为利润函数,记为P(x).
(1)设C(x)=10-6x3-0.003x2+5x+1000,
生产多少单位产品时,边际成本C′(X)最低?
(2)设C(x)=50x+10000,产品的单价
p=100-0.01x,怎样定价,可使利润最大?
阅读P 15 : 链接---边际函数
有一隧道既是交通拥挤地段,又是事故多发地段.为了保证安全,交通部门规定,隧道内的车距d(m)正比于车速v(km/h)的平方与自身长L(m)的积,且车距不得小于半个车身长,而当车速为60(km/h)时,车距为1.44个车身长.在交通繁忙时,应规定怎样的车速,可以使隧道的车流量最大?
课堂练习:
P38/4
生产某塑料管的利润函数为P(n)=-n3+600n2+67500n-1200000,其中n为工厂每月生产该塑料管的根数,利润P(n)的单位为元.
(1)求边际利润函数P′(n);
(2)求使P′(n)=0的值;
(3)解释(2)中的n值的实际意义.
