导数的应用(82)
图片预览







文档简介
(共26张PPT)
3. 函数f(x)=x+ 的极小值为___.
4、若函数y=x3+ax在R上有极值点,则a的取值范围是______.
作业79
80讲7.曲线y=3x5-5x3共有___________个极值.
8、已知函数 ,则f(1)与f(-1)的大小关系是_____.
4.函数y= 的最大值为__
作业81
5.设y=|x|3,那么y在区间[-3,-1]上的最小值是______
6.设f(x)=ax3-6ax2+b在区间[-1, 2]上的最大值为3, 最小值为-29, 且a>b, 则a=____, b=___.
作业81
7.点P是曲线y=x2-lnx上任意一点, 则点P到直线y=x-2的距离的最小值是__________.
80讲7.曲线y=3x5-5x3共有___________个极值.
导数在实际生活中的应用
新课引入:
导数在实际生活中有着广泛的应用,利用导数求最值的方法,可以求出实际生活中的某些最值问题.
1.几何方面的应用
2.物理方面的应用.
3.经济学方面的应用
(面积和体积等的最值)
(利润方面最值)
(功和功率等最值)
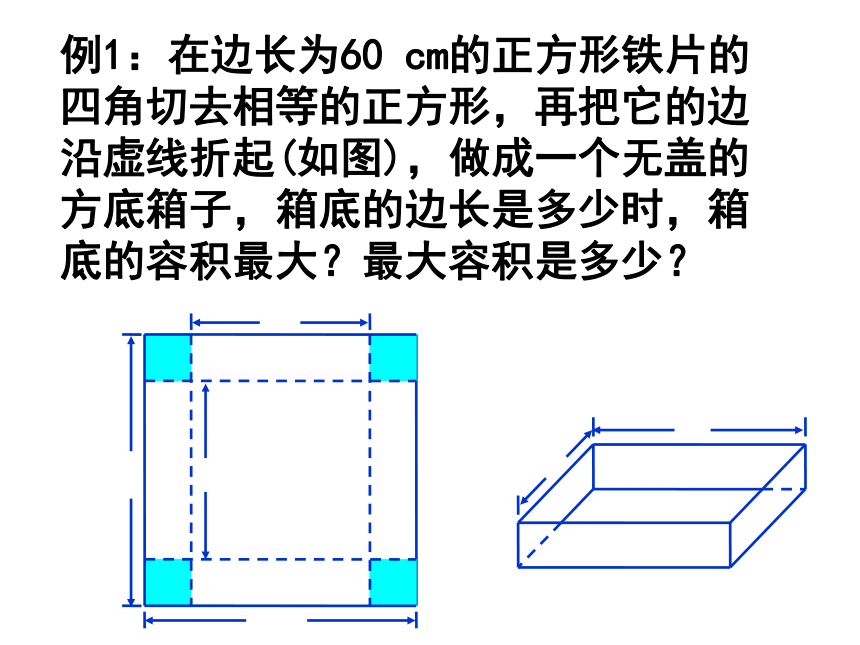
例1:在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
由题意可知,当x过小(接近0)或过大(接近60)时,箱子容积很小,因此,16000是最大值。
答:当x=40cm时,箱子容积最大,最大容积是16 000cm3
解法:设箱底边长为xcm,则箱高 cm,
令 ,解得 x=0(舍去),x=40,
并求得 V(40)=16000
3、求最大(最小)值应用题的一般方法
(1)分析实际问题中各量之间的关系,把实际问题化为数学问题,建立函数关系式,这是关键一步。
(2)确定函数定义域,并求出极值点。
(3)比较各极值与定义域端点函数的大小, 结合实际,确定最值或最值点。
实际应用问题的表现形式,常常不是以纯数学模式反映出来。
首先,通过审题,认识问题的背景,抽象出问题的实质。其次,建立相应的数学模型, 将应用问题转化为数学问题,再解。
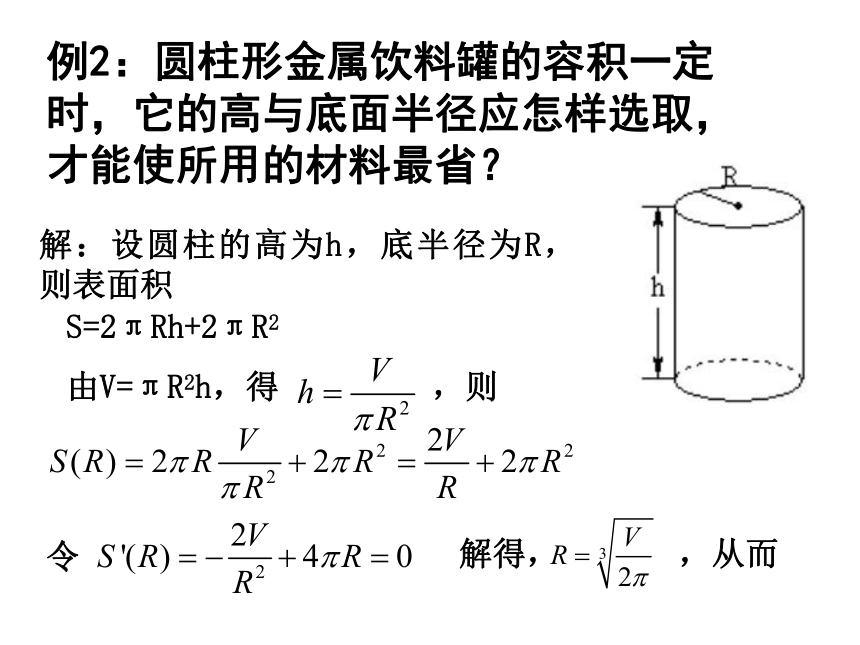
解:设圆柱的高为h,底半径为R,则表面积
例2:圆柱形金属饮料罐的容积一定时,它的高与底面半径应怎样选取,才能使所用的材料最省?
S=2πRh+2πR2
由V=πR2h,得 ,则
令
解得, ,从而
答:当罐的高与底直径相等时,所用材料最省
即 h=2R
因为S(R)只有一个极值,所以它是最小值
变式:当圆柱形金属饮料罐的表面积为定值S时,它的高与底面半径应怎样选取,才能使体积最大?
h
R
例3:已知某商品生产总成本C与产量q的函数关系式为C=100+4q,每件价格p与产量q的函数关系式为 ,求产量q为何值时,利润L最大?
分析:利润L等于收入R减去成本C,而收入R等于产量乘价格.由此可得出利润L与产量q的函数关系式,再用导数求最大利润.
解:收入
答:产量为84时,利润L最大。
令 ,即 ,求得唯一的极值点
利润
如何解决优化问题
优化问题
优化问题的答案
用函数表示的数学问题
用导数解决数学问题
例2.已知函数f(x)=ax3+bx2+cx在x0处取得极大值5 ,其导函数y=f '(x)的图象经过点(1,0), (2,0), 如图, 求: (1)x0及函数f(x)解析式;
(2)设g(x)=f(x)+m, 若对于 x [0,2]不等式g(x)数学应用
变1.讨论方程f(x)=k的实根个数;
变2.若函数y=f(x)在[m,n]上的值域为 [4,9],求m,n满足的条件;
问题3:
饮料瓶大小对饮料公司利润有影响吗
你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些 你想从数学上知道它的道理吗
是不是饮料瓶越大,饮料公司的利润越大
例如:
某制造商制造并出售球形瓶装饮料.瓶子制造成本是0.8πr2分.已知每出售1ml的饮料,可获利0.2分,且瓶子的最大半径为6cm.
1)瓶子半径多大时,能使每瓶饮料的 利润最大?
2)瓶子半径多大时,每瓶饮料的利润最小?
例2.已知函数f(x)=ax3+bx2+cx在x0处取得极大值5 ,其导函数y=f '(x)的图象经过点(1,0), (2,0), 如图, 求: (1)x0及函数f(x)解析式;
(2)设g(x)=f(x)+m, 若对于 x [0,2]不等式g(x)数学应用
变1.讨论方程f(x)=k的实根个数;
变2.若函数y=f(x)在[m,n]上的值域为 [4,9],求m,n满足的条件;
(作业第8题)
x
y
练习1: 如图,在二次函数f(x)=4x-x2的图象与x轴所
围成的图形中有一个内接矩形ABCD,求这 个矩形的最大面积.
解:设B(x,0)(0A(x, 4x-x2).
从而|AB|= 4x-x2,|BC|=2(2-x).故矩形ABCD的面积
为:S(x)=|AB||BC|=2x3-12x2+16x(0令 ,得
所以当 时,
因此当点B为 时,矩形的最大面积是
2、 一艘轮船在航行中的燃料费和它的速度的立方成正比。已知在速度为10km/h时,燃料费是6元/h。而其他与速度无关的费用为96元/h。问以何种速度航行时。能使行驶每公里的费用总和最少?
3、如图,铁路线上AB段长
100km,工厂C到铁路的
距离CA=20km.现在要
在AB上某一处D,向C修
一条公路.已知铁路每吨
千米与公路每吨千米的运费之比为3:5.为了使原料
从供应站B运到工厂C的运费最省,D应修在何处
B D A
C
解:设DA=xkm,那么DB=(100-x)km,CD=
km.
又设铁路上每吨千米的运费为3t元,则公路上每吨千米的运费为5t元.这样,每吨原料从供应站B运到工厂C的总运费为
令 ,在 的范围内有
唯一解x=15.
所以,当x=15(km),即D点选在距A点15千米时,总运费最省.
注:可以进一步讨论,当AB的距离大于15千米时,要找的
最优点总在距A点15千米的D点处;当AB之间的距离
不超过15千米时,所选D点与B点重合.
练习4:已知圆锥的底面半径为R,高为H,求内接于这个圆锥体并且体积最大的圆柱体的高h.
答:设圆柱底面半径为r,可得r=R(H-h)/H.易得当h=H/3
时, 圆柱体的体积最大.
例4如图,扇形AOB中,半径0A=1,∠AOB=900,
在OA的延长线上有一动点C,过C作CD与弧AB相
切于点E,且与过点B所作的OB的垂线交于点D,
当点C在什么位置时,直角梯形OCDB的面积最小?
O
B
D
E
C
A
注:在实际问题中,若
函数在区间内只有一个
点使y’=0,如果函数在这
点有极值,那么不与端
点比较,就可确定这个
点就是最值。
1、实际问题中的应用.
在日常生活、生产和科研中,常常会遇到求函数的
最大(小)值的问题.建立目标函数,然后利用导数的方法求最值是求解这类问题常见的解题思路.
在建立目标函数时,一定要注意确定函数的定义域.
在实际问题中,有时会遇到函数在区间内只有一个点使 的情形,如果函数在这个点有极大(小)值,
那么不与端点值比较,也可以知道这就是最大(小)值.
这里所说的也适用于开区间或无穷区间.
满足上述情况的函数我们称之为“单峰函数”.
3. 函数f(x)=x+ 的极小值为___.
4、若函数y=x3+ax在R上有极值点,则a的取值范围是______.
作业79
80讲7.曲线y=3x5-5x3共有___________个极值.
8、已知函数 ,则f(1)与f(-1)的大小关系是_____.
4.函数y= 的最大值为__
作业81
5.设y=|x|3,那么y在区间[-3,-1]上的最小值是______
6.设f(x)=ax3-6ax2+b在区间[-1, 2]上的最大值为3, 最小值为-29, 且a>b, 则a=____, b=___.
作业81
7.点P是曲线y=x2-lnx上任意一点, 则点P到直线y=x-2的距离的最小值是__________.
80讲7.曲线y=3x5-5x3共有___________个极值.
导数在实际生活中的应用
新课引入:
导数在实际生活中有着广泛的应用,利用导数求最值的方法,可以求出实际生活中的某些最值问题.
1.几何方面的应用
2.物理方面的应用.
3.经济学方面的应用
(面积和体积等的最值)
(利润方面最值)
(功和功率等最值)
例1:在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
由题意可知,当x过小(接近0)或过大(接近60)时,箱子容积很小,因此,16000是最大值。
答:当x=40cm时,箱子容积最大,最大容积是16 000cm3
解法:设箱底边长为xcm,则箱高 cm,
令 ,解得 x=0(舍去),x=40,
并求得 V(40)=16000
3、求最大(最小)值应用题的一般方法
(1)分析实际问题中各量之间的关系,把实际问题化为数学问题,建立函数关系式,这是关键一步。
(2)确定函数定义域,并求出极值点。
(3)比较各极值与定义域端点函数的大小, 结合实际,确定最值或最值点。
实际应用问题的表现形式,常常不是以纯数学模式反映出来。
首先,通过审题,认识问题的背景,抽象出问题的实质。其次,建立相应的数学模型, 将应用问题转化为数学问题,再解。
解:设圆柱的高为h,底半径为R,则表面积
例2:圆柱形金属饮料罐的容积一定时,它的高与底面半径应怎样选取,才能使所用的材料最省?
S=2πRh+2πR2
由V=πR2h,得 ,则
令
解得, ,从而
答:当罐的高与底直径相等时,所用材料最省
即 h=2R
因为S(R)只有一个极值,所以它是最小值
变式:当圆柱形金属饮料罐的表面积为定值S时,它的高与底面半径应怎样选取,才能使体积最大?
h
R
例3:已知某商品生产总成本C与产量q的函数关系式为C=100+4q,每件价格p与产量q的函数关系式为 ,求产量q为何值时,利润L最大?
分析:利润L等于收入R减去成本C,而收入R等于产量乘价格.由此可得出利润L与产量q的函数关系式,再用导数求最大利润.
解:收入
答:产量为84时,利润L最大。
令 ,即 ,求得唯一的极值点
利润
如何解决优化问题
优化问题
优化问题的答案
用函数表示的数学问题
用导数解决数学问题
例2.已知函数f(x)=ax3+bx2+cx在x0处取得极大值5 ,其导函数y=f '(x)的图象经过点(1,0), (2,0), 如图, 求: (1)x0及函数f(x)解析式;
(2)设g(x)=f(x)+m, 若对于 x [0,2]不等式g(x)
变1.讨论方程f(x)=k的实根个数;
变2.若函数y=f(x)在[m,n]上的值域为 [4,9],求m,n满足的条件;
问题3:
饮料瓶大小对饮料公司利润有影响吗
你是否注意过,市场上等量的小包装的物品一般比大包装的要贵些 你想从数学上知道它的道理吗
是不是饮料瓶越大,饮料公司的利润越大
例如:
某制造商制造并出售球形瓶装饮料.瓶子制造成本是0.8πr2分.已知每出售1ml的饮料,可获利0.2分,且瓶子的最大半径为6cm.
1)瓶子半径多大时,能使每瓶饮料的 利润最大?
2)瓶子半径多大时,每瓶饮料的利润最小?
例2.已知函数f(x)=ax3+bx2+cx在x0处取得极大值5 ,其导函数y=f '(x)的图象经过点(1,0), (2,0), 如图, 求: (1)x0及函数f(x)解析式;
(2)设g(x)=f(x)+m, 若对于 x [0,2]不等式g(x)
变1.讨论方程f(x)=k的实根个数;
变2.若函数y=f(x)在[m,n]上的值域为 [4,9],求m,n满足的条件;
(作业第8题)
x
y
练习1: 如图,在二次函数f(x)=4x-x2的图象与x轴所
围成的图形中有一个内接矩形ABCD,求这 个矩形的最大面积.
解:设B(x,0)(0
从而|AB|= 4x-x2,|BC|=2(2-x).故矩形ABCD的面积
为:S(x)=|AB||BC|=2x3-12x2+16x(0
所以当 时,
因此当点B为 时,矩形的最大面积是
2、 一艘轮船在航行中的燃料费和它的速度的立方成正比。已知在速度为10km/h时,燃料费是6元/h。而其他与速度无关的费用为96元/h。问以何种速度航行时。能使行驶每公里的费用总和最少?
3、如图,铁路线上AB段长
100km,工厂C到铁路的
距离CA=20km.现在要
在AB上某一处D,向C修
一条公路.已知铁路每吨
千米与公路每吨千米的运费之比为3:5.为了使原料
从供应站B运到工厂C的运费最省,D应修在何处
B D A
C
解:设DA=xkm,那么DB=(100-x)km,CD=
km.
又设铁路上每吨千米的运费为3t元,则公路上每吨千米的运费为5t元.这样,每吨原料从供应站B运到工厂C的总运费为
令 ,在 的范围内有
唯一解x=15.
所以,当x=15(km),即D点选在距A点15千米时,总运费最省.
注:可以进一步讨论,当AB的距离大于15千米时,要找的
最优点总在距A点15千米的D点处;当AB之间的距离
不超过15千米时,所选D点与B点重合.
练习4:已知圆锥的底面半径为R,高为H,求内接于这个圆锥体并且体积最大的圆柱体的高h.
答:设圆柱底面半径为r,可得r=R(H-h)/H.易得当h=H/3
时, 圆柱体的体积最大.
例4如图,扇形AOB中,半径0A=1,∠AOB=900,
在OA的延长线上有一动点C,过C作CD与弧AB相
切于点E,且与过点B所作的OB的垂线交于点D,
当点C在什么位置时,直角梯形OCDB的面积最小?
O
B
D
E
C
A
注:在实际问题中,若
函数在区间内只有一个
点使y’=0,如果函数在这
点有极值,那么不与端
点比较,就可确定这个
点就是最值。
1、实际问题中的应用.
在日常生活、生产和科研中,常常会遇到求函数的
最大(小)值的问题.建立目标函数,然后利用导数的方法求最值是求解这类问题常见的解题思路.
在建立目标函数时,一定要注意确定函数的定义域.
在实际问题中,有时会遇到函数在区间内只有一个点使 的情形,如果函数在这个点有极大(小)值,
那么不与端点值比较,也可以知道这就是最大(小)值.
这里所说的也适用于开区间或无穷区间.
满足上述情况的函数我们称之为“单峰函数”.
