人教版数学八年级下册18.1 --18.2:同步测试题 (Word版 含答案)
文档属性
| 名称 | 人教版数学八年级下册18.1 --18.2:同步测试题 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 378.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 23:32:25 | ||
图片预览



文档简介
18.1平行四边形的性质和判定
班级___________ 姓名_________得分 ________
一、巩固训练:
1.平行四边形长边是短边的2倍,一条对角线与短边垂直,则这个平行四边形各角的度数分别为______.
2.从平行四边形的一个锐角顶点作两条高线,如果这两条高线夹角为135°,则这个平行四边形的各内角的度数为______.
3.在ABCD中,BC=2AB,若E为BC的中点,则∠AED=______.
4.在ABCD中,如果一边长为8cm,一条对角线为6cm,则另一条对角线x的取值范围是______.
5.如图,在ABCD中,M是BC的中点,且AM=9,BD=12,
AD=10,则ABCD的面积是______.
6.ABCD中,对角线AC、BD交于O,且AB=AC=2cm,若∠ABC=60°,则△OAB的周长为______cm.
7.如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AF=5,,则△CEF的周长为______.
8.如图,BD为ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC______S△BNC.(填“<”、“=”或“>”)
9.ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AD=7,BD=10,则ABCD的面积为______.
10.如图,在△ABC中,EF为△ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连结EF、DF,要使四边形AEDF为平行四边形,需要添加条件____________.(只添加一个条件)
二、提高训练:
1、如图,ABCD中,E、F是直线AC上两点,且AE=CF.
求证:(1)BE=DF;(2)BE∥DF.
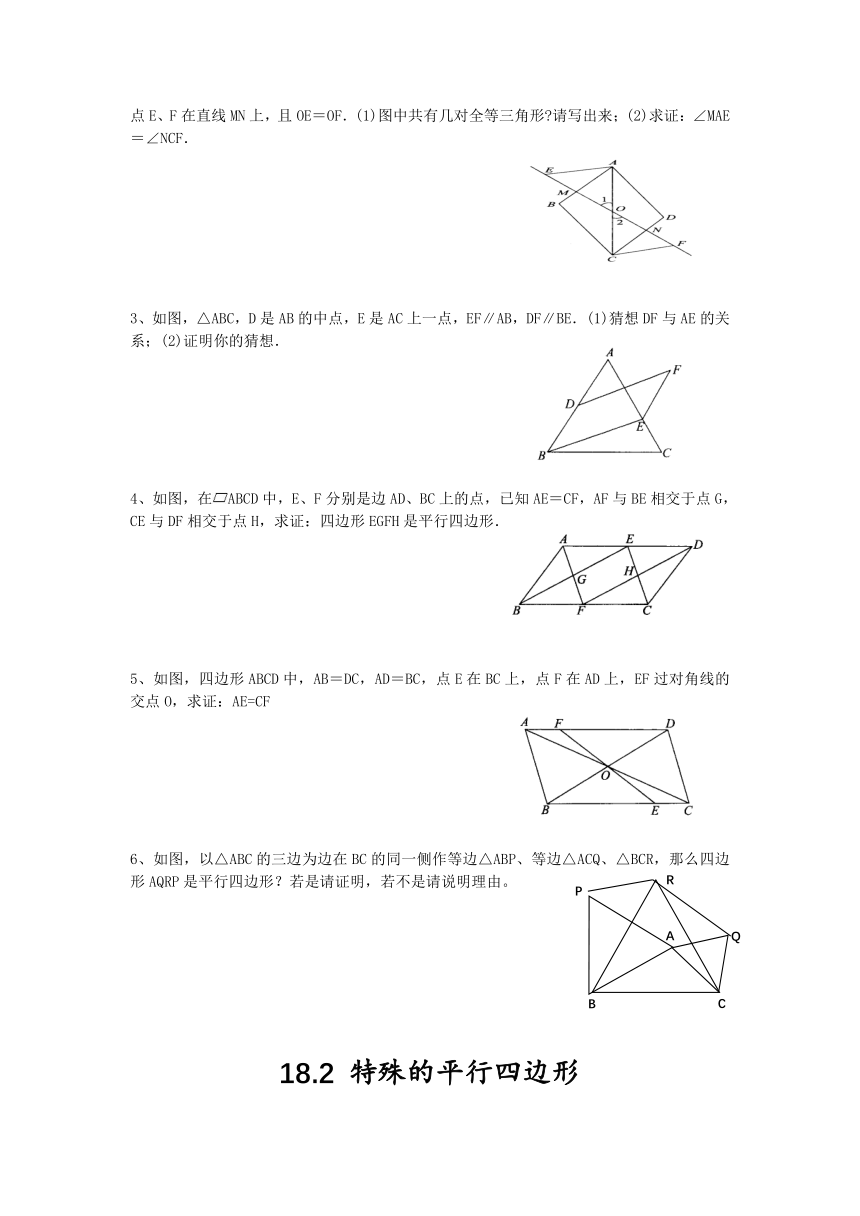
2、如图,O为ABCD的对角线AC的串点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.(1)图中共有几对全等三角形?请写出来;(2)求证:∠MAE=∠NCF.
3、如图,△ABC,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE.(1)猜想DF与AE的关系;(2)证明你的猜想.
4、如图,在ABCD中,E、F分别是边AD、BC上的点,已知AE=CF,AF与BE相交于点G,CE与DF相交于点H,求证:四边形EGFH是平行四边形.
5、如图,四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,EF过对角线的交点O,求证:AE=CF
6、如图,以△ABC的三边为边在BC的同一侧作等边△ABP、等边△ACQ、△BCR,那么四边形AQRP是平行四边形?若是请证明,若不是请说明理由。
18.2 特殊的平行四边形
一、选择题
1. 如图,在菱形中,,,则菱形的边长为( )
A. B. C. D.
2. 如图,在矩形ABCD中,点E,F在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明.
3. 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=2∶1,则线段CH的长是( )
A. 3 B. 4 C. 5 D. 6
4. (2020·黑龙江龙东)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.72 B.24 C.48 D.96
5. (3分)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2 B. C.3 D.4
6. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
A. 2 B. C. D. 1
7. 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:
①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若=,则3S△EDH=13S△DHC,其中结论正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
8. (2020·东营)如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N,下列结论:①△APE≌△AME;②PM+PN=AC;③;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是( )
A. ①②③④ B. ①②③⑤ C. ①②③④⑤ D. ③④⑤
二、填空题
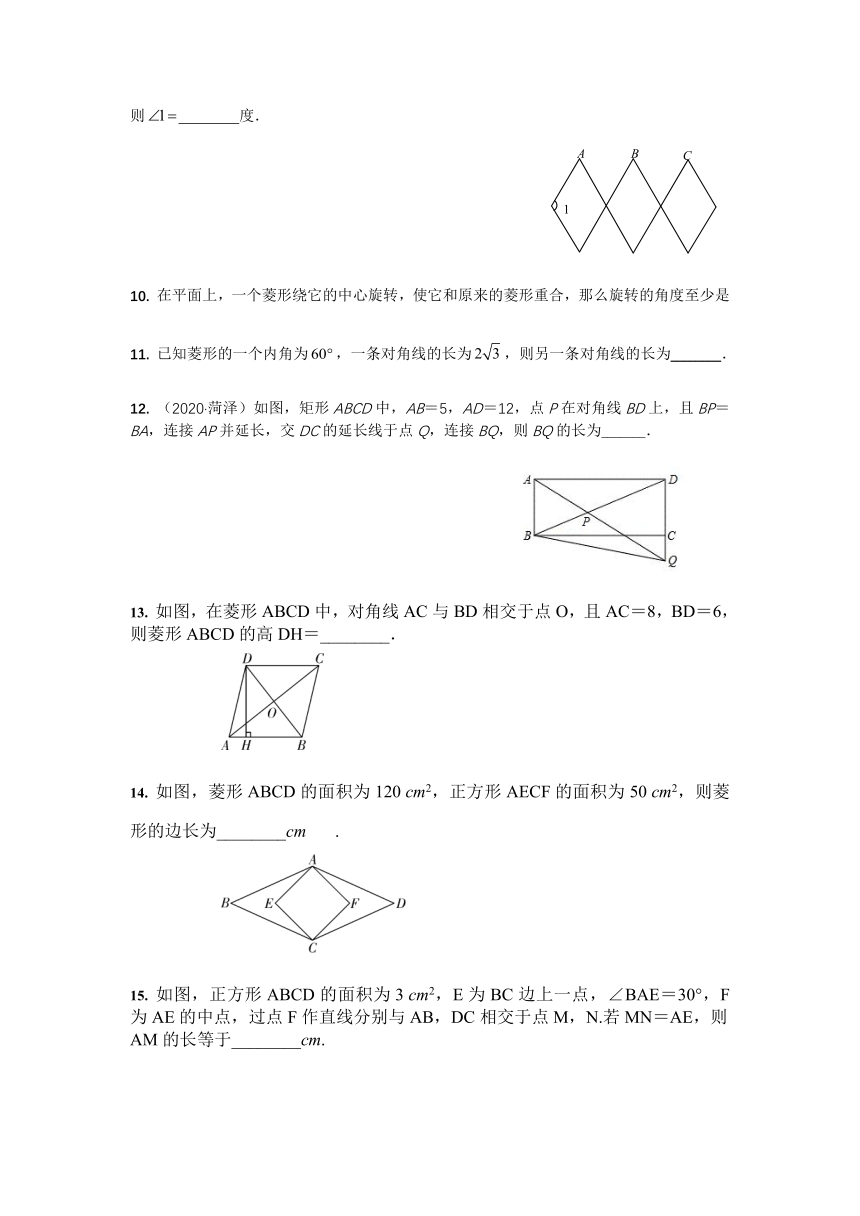
9. 如图,一活动菱形衣架中,菱形的边长均为若墙上钉子间的距离,则 度.
10. 在平面上,一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是
11. 已知菱形的一个内角为,一条对角线的长为,则另一条对角线的长为________.
12. (2020·菏泽)如图,矩形ABCD中,AB=5,AD=12,点P在对角线BD上,且BP=BA,连接AP并延长,交DC的延长线于点Q,连接BQ,则BQ的长为_______.
13. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=________.
14. 如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为________cm.
15. 如图,正方形ABCD的面积为3 cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于________cm.
16. 如图,是边长为的正方形,是内接于的正方形,,若则=
三、解答题
17. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
18. 如图,平行四边形中,、、、分别是、、、的平分线,与交于,与交于,证明:四边形是矩形.
人教版 八年级数学 18.2 特殊的平行四边形 课时训练-答案
一、选择题
1. 【答案】A
【解析】由菱形的对角线互相垂直平分及勾股数可知选A
2. 【答案】添加的条件是BE=DF(答案不唯一).
证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠ABD=∠BDC,
又∵BE=DF(添加),
∴△ABE≌△CDF(SAS),
∴AE=CF.
3. 【答案】B 【解析】设CH=x,∵BE∶EC=2∶1,BC=9,∴EC=3,由折叠可知,EH=DH=9-x,在Rt△ECH中,由勾股定理得:(9-x)2=32+x2,解得:x=4.
4. 【答案】 C
【解析】本题考查了菱形的性质,对角线互相垂直平分以及直角三角形的斜边上中线的性质,解:∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD,
∵DH⊥AB,∴∠BHD=90°,∴BD=2OH,∵OH=4,∴BD=8,
∵OA=6,∴AC=12,∴菱形ABCD的面积.故选:C.
5. 【答案】B
【解析】根据菱形的对角线互相垂直平分求出OB,OC,AC⊥BD,然后利用勾股定理列式求出BC,最后根据三角形的中位线平行于第三边并且等于第三边的一半求解即可.
∵菱形ABCD的对角线AC、BD相交于点O,
∴OBBD6=3,OA=OCAC8=4,AC⊥BD,
由勾股定理得,BC5,
∴AD=5,
∵OE=CE,
∴∠DCA=∠EOC,
∵四边形ABCD是菱形,
∴∠DCA=∠DAC,
∴∠DAC=∠EOC,
∴OE∥AD,
∵AO=OC,
∴OE是△ADC的中位线,
∴OEAD=2.5.
6. 【答案】B 【解析】∵AB=2,∴BF=2,又∵BM=BC=1,由勾股定理得FM==.
7. 【答案】D 【解析】逐项分析如下表:
序号 逐项分析 正误
① 在正方形ABCD中,AB=BC=CD=DA,∠DAB=∠B=∠BCD=∠CDA=90°,∠ACB=∠ACD=45°,∵EF∥AD,∴四边形EFDA、四边形EFCB是矩形,∴∠EFC=∠ADC=90°,EF=DC,在Rt△CGF中,∠ACD=45°,∴GF=CF,∴EF-GF=CD-CF,即EG=DF √
② ∵△GFC是等腰直角三角形,H是CG的中点,∴GH=FH,∠HGF=∠GFH=45°,∴∠EGH=∠DFH=135°,又由①知EG=DF,∴△EGH≌△DFH(SAS),∴∠HEF=∠FDH,∵∠AEH=∠AEF+∠HEF=90°+∠HEF,∠ADH=∠ADC-∠FDH=90°-∠FDH,∴∠AEH+∠ADH=180° √
③ 由②可知EH=DH,FH=CH,又∵EF=DC,∴△EHF≌△DHC(SSS) √
④ ∵△EGH≌△DFH,∴EH=DH,∠EHG=∠DHF,∴∠EHG+∠AHD=∠DHF+∠AHD=90°,即∠EHD=∠AHF=90°,∴△EHD为等腰直角三角形,∵=,∴设AE=2x,AB=3x,则DE==x,∴EH=DH=×x=x,∴S△EDH=EH2=×x2=x2. 在△DHC中,设CD边上的高为h,则h=CF=,则S△DHC=CD·h=×3x×=x2,==,即3S△EDH=13S△DHC √
8. 【答案】B
【解析】本题考查了垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质,是常见问题的综合,灵活的运用所学知识是解答本题的关键.综合应用垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质等知识,逐个判断5个结论的正确性,得出结论.
①∵正方形ABCD,∴∠APE=∠AME=45°,∵PM⊥AE,∴∠AEP=∠AEM=90°,∵AE=AE,∴△APE≌△AME(ASA);
②过点N作NQ⊥AC于点Q,则四边形PNQE是矩形,∴PN=EQ,∵正方形ABCD,∴∠PAE=∠MAE=45°,∵PM⊥AE,∴∠PEA=45°,∴∠PAE=∠APE,PE=NQ,∴△APE等腰直角三角形,∴AE=PE,同理得:△NQC等腰直角三角形,∴NQ=CQ,∵△APE≌△AME,∴PE=ME,∴PE=ME= NQ=CQ,∴PM=AE+CQ,∴PM+PN=AE+CQ+EQ=AC,即PM+PN=AC成立;
③∵正方形ABCD,∴AC⊥BD,∴∠EOF是直角,∵过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,∴∠PEO和∠PFO是直角,∴四边形PFOE是矩形,∴PF=OE,在Rt△PEO中,有PE2+OE2=PO2,∴PE2+PF2=PO2,即PE2+PF2=PO2成立;
④△BNF是等腰直角三角形,点P不在AB的中点时,△POF不是等腰直角三角形,所以△POF与△BNF不一定相似,即△POF∽△BNF不一定成立;
⑤∵△AMP是等腰直角三角形,△PMN∽△AMP,∴△PMN是等腰直角三角形,∵∠MPN=90°,∴PM=PN,∵AP=PM,BP=PN,∴AP=BP,∴点P是AB的中点,又∵O为正方形的对称中点,∴点O在M、N两点的连线上.综上,①②③⑤成立,即正确的结论有4个,答案选B.
二、填空题
9. 【答案】
【解析】由题意可知:构成三角形为等边三角形
10. 【答案】
【解析】根据菱形的性质可知:应当旋转至少
11. 【答案】或
12. 【答案】3
【解析】由于已知BC的长,故可设想在Rt△BCQ中利用勾股定理求解,则需求CQ的长,这可通过求DQ的长得到,结合已知条件BP=BA=5,易知DQ=DP,显然DP可求,思路沟通.
在矩形ABCD中,∠BAD=90?,AB=5,AD=12,∴BD==13,又∵BP=BA=5,∴DP=13-5=8,∠BAP=∠BPA.∵AB∥DQ,∴∠BAP=∠PQD,∴∠PQD=∠BPA=∠DPQ,∴DQ=DP=8,∴CQ=8-5=3.在Rt△BCQ中,BC=12,CQ=3,∴BQ==3.
13. 【答案】4.8 【解析】∵S菱形=AC·BD=2AB·DH,∴AC·BD=2AB·DH.∵四边形ABCD是菱形,∴∠AOB=90°,AO=AC=4,BO=BD=3,∴在Rt△AOB中,AB==5,∴DH==4.8.
14. 【答案】13 【解析】如解图,连接AC、BD交于O,则有AC·BD=120,∴AC·BD=240,又∵菱形对角线互相垂直平分,∴2OA·2OB=240,∴ OA·OB=60,∵AE2=50, OA2+OE2= AE2,OA=OE,∴OA=5,∴OB=12,∴AB===13.
解图
15. 【答案】或 【解析】如解图,过N作NG⊥AB,交AB于点G,∵四边形ABCD为正方形,∴AB=AD=NG= cm,在Rt△ABE中,∠BAE=30°,AB= cm,∴BE=1 cm,AE=2 cm,∵F为AE的中点,∴AF=AE=1 cm,在Rt△ABE和Rt△NGM中,,∴Rt△ABE≌Rt△NGM(HL),∴BE=GM,∠BAE=∠MNG=30°,∠AEB=∠NMG=60°,∴∠AFM=90°,即MN⊥AE,在Rt△AMF中,∠FAM=30°,AF=1 cm,∴AM=== cm,由对称性得到AM′=BM=AB-AM=-= cm,综上,AM的长等于或 cm.
解图
16. 【答案】
【解析】,则,所以得到
三、解答题
17. 【答案】
解:(1)证明:∵E是AD的中点,∴AE=DE,
又∵AF∥BC,
∴∠AFE=∠DBE,∠EAF=∠EDB,
∴△AEF≌△DEB.
(2)四边形ADCF是矩形.
证明:∵AF∥CD,AF=CD,
∴四边形ADCF是平行四边形.
∵△AEF≌△DEB,∴AF=BD,
∴BD=CD,即AD是△ABC的中线,
又∵AB=AC,∴AD⊥BC,
∴∠ADC=90°.
∴四边形ADCF是矩形.
18. 【答案】
∵四边形为平行四边形
∴,
∵、分别是、的平分线
∴
∴
同理
∴四边形是矩形.
班级___________ 姓名_________得分 ________
一、巩固训练:
1.平行四边形长边是短边的2倍,一条对角线与短边垂直,则这个平行四边形各角的度数分别为______.
2.从平行四边形的一个锐角顶点作两条高线,如果这两条高线夹角为135°,则这个平行四边形的各内角的度数为______.
3.在ABCD中,BC=2AB,若E为BC的中点,则∠AED=______.
4.在ABCD中,如果一边长为8cm,一条对角线为6cm,则另一条对角线x的取值范围是______.
5.如图,在ABCD中,M是BC的中点,且AM=9,BD=12,
AD=10,则ABCD的面积是______.
6.ABCD中,对角线AC、BD交于O,且AB=AC=2cm,若∠ABC=60°,则△OAB的周长为______cm.
7.如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AF=5,,则△CEF的周长为______.
8.如图,BD为ABCD的对角线,M、N分别在AD、AB上,且MN∥BD,则S△DMC______S△BNC.(填“<”、“=”或“>”)
9.ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AD=7,BD=10,则ABCD的面积为______.
10.如图,在△ABC中,EF为△ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连结EF、DF,要使四边形AEDF为平行四边形,需要添加条件____________.(只添加一个条件)
二、提高训练:
1、如图,ABCD中,E、F是直线AC上两点,且AE=CF.
求证:(1)BE=DF;(2)BE∥DF.
2、如图,O为ABCD的对角线AC的串点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.(1)图中共有几对全等三角形?请写出来;(2)求证:∠MAE=∠NCF.
3、如图,△ABC,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE.(1)猜想DF与AE的关系;(2)证明你的猜想.
4、如图,在ABCD中,E、F分别是边AD、BC上的点,已知AE=CF,AF与BE相交于点G,CE与DF相交于点H,求证:四边形EGFH是平行四边形.
5、如图,四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,EF过对角线的交点O,求证:AE=CF
6、如图,以△ABC的三边为边在BC的同一侧作等边△ABP、等边△ACQ、△BCR,那么四边形AQRP是平行四边形?若是请证明,若不是请说明理由。
18.2 特殊的平行四边形
一、选择题
1. 如图,在菱形中,,,则菱形的边长为( )
A. B. C. D.
2. 如图,在矩形ABCD中,点E,F在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明.
3. 如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH,若BE∶EC=2∶1,则线段CH的长是( )
A. 3 B. 4 C. 5 D. 6
4. (2020·黑龙江龙东)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.72 B.24 C.48 D.96
5. (3分)如图,四边形ABCD是菱形,对角线AC,BD相交于点O,AC=8.BD=6,点E是CD上一点,连接OE,若OE=CE,则OE的长是( )
A.2 B. C.3 D.4
6. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若AB的长为2,则FM的长为( )
A. 2 B. C. D. 1
7. 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:
①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若=,则3S△EDH=13S△DHC,其中结论正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
8. (2020·东营)如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N,下列结论:①△APE≌△AME;②PM+PN=AC;③;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是( )
A. ①②③④ B. ①②③⑤ C. ①②③④⑤ D. ③④⑤
二、填空题
9. 如图,一活动菱形衣架中,菱形的边长均为若墙上钉子间的距离,则 度.
10. 在平面上,一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是
11. 已知菱形的一个内角为,一条对角线的长为,则另一条对角线的长为________.
12. (2020·菏泽)如图,矩形ABCD中,AB=5,AD=12,点P在对角线BD上,且BP=BA,连接AP并延长,交DC的延长线于点Q,连接BQ,则BQ的长为_______.
13. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD的高DH=________.
14. 如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为________cm.
15. 如图,正方形ABCD的面积为3 cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于________cm.
16. 如图,是边长为的正方形,是内接于的正方形,,若则=
三、解答题
17. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
18. 如图,平行四边形中,、、、分别是、、、的平分线,与交于,与交于,证明:四边形是矩形.
人教版 八年级数学 18.2 特殊的平行四边形 课时训练-答案
一、选择题
1. 【答案】A
【解析】由菱形的对角线互相垂直平分及勾股数可知选A
2. 【答案】添加的条件是BE=DF(答案不唯一).
证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠ABD=∠BDC,
又∵BE=DF(添加),
∴△ABE≌△CDF(SAS),
∴AE=CF.
3. 【答案】B 【解析】设CH=x,∵BE∶EC=2∶1,BC=9,∴EC=3,由折叠可知,EH=DH=9-x,在Rt△ECH中,由勾股定理得:(9-x)2=32+x2,解得:x=4.
4. 【答案】 C
【解析】本题考查了菱形的性质,对角线互相垂直平分以及直角三角形的斜边上中线的性质,解:∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD,
∵DH⊥AB,∴∠BHD=90°,∴BD=2OH,∵OH=4,∴BD=8,
∵OA=6,∴AC=12,∴菱形ABCD的面积.故选:C.
5. 【答案】B
【解析】根据菱形的对角线互相垂直平分求出OB,OC,AC⊥BD,然后利用勾股定理列式求出BC,最后根据三角形的中位线平行于第三边并且等于第三边的一半求解即可.
∵菱形ABCD的对角线AC、BD相交于点O,
∴OBBD6=3,OA=OCAC8=4,AC⊥BD,
由勾股定理得,BC5,
∴AD=5,
∵OE=CE,
∴∠DCA=∠EOC,
∵四边形ABCD是菱形,
∴∠DCA=∠DAC,
∴∠DAC=∠EOC,
∴OE∥AD,
∵AO=OC,
∴OE是△ADC的中位线,
∴OEAD=2.5.
6. 【答案】B 【解析】∵AB=2,∴BF=2,又∵BM=BC=1,由勾股定理得FM==.
7. 【答案】D 【解析】逐项分析如下表:
序号 逐项分析 正误
① 在正方形ABCD中,AB=BC=CD=DA,∠DAB=∠B=∠BCD=∠CDA=90°,∠ACB=∠ACD=45°,∵EF∥AD,∴四边形EFDA、四边形EFCB是矩形,∴∠EFC=∠ADC=90°,EF=DC,在Rt△CGF中,∠ACD=45°,∴GF=CF,∴EF-GF=CD-CF,即EG=DF √
② ∵△GFC是等腰直角三角形,H是CG的中点,∴GH=FH,∠HGF=∠GFH=45°,∴∠EGH=∠DFH=135°,又由①知EG=DF,∴△EGH≌△DFH(SAS),∴∠HEF=∠FDH,∵∠AEH=∠AEF+∠HEF=90°+∠HEF,∠ADH=∠ADC-∠FDH=90°-∠FDH,∴∠AEH+∠ADH=180° √
③ 由②可知EH=DH,FH=CH,又∵EF=DC,∴△EHF≌△DHC(SSS) √
④ ∵△EGH≌△DFH,∴EH=DH,∠EHG=∠DHF,∴∠EHG+∠AHD=∠DHF+∠AHD=90°,即∠EHD=∠AHF=90°,∴△EHD为等腰直角三角形,∵=,∴设AE=2x,AB=3x,则DE==x,∴EH=DH=×x=x,∴S△EDH=EH2=×x2=x2. 在△DHC中,设CD边上的高为h,则h=CF=,则S△DHC=CD·h=×3x×=x2,==,即3S△EDH=13S△DHC √
8. 【答案】B
【解析】本题考查了垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质,是常见问题的综合,灵活的运用所学知识是解答本题的关键.综合应用垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质等知识,逐个判断5个结论的正确性,得出结论.
①∵正方形ABCD,∴∠APE=∠AME=45°,∵PM⊥AE,∴∠AEP=∠AEM=90°,∵AE=AE,∴△APE≌△AME(ASA);
②过点N作NQ⊥AC于点Q,则四边形PNQE是矩形,∴PN=EQ,∵正方形ABCD,∴∠PAE=∠MAE=45°,∵PM⊥AE,∴∠PEA=45°,∴∠PAE=∠APE,PE=NQ,∴△APE等腰直角三角形,∴AE=PE,同理得:△NQC等腰直角三角形,∴NQ=CQ,∵△APE≌△AME,∴PE=ME,∴PE=ME= NQ=CQ,∴PM=AE+CQ,∴PM+PN=AE+CQ+EQ=AC,即PM+PN=AC成立;
③∵正方形ABCD,∴AC⊥BD,∴∠EOF是直角,∵过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,∴∠PEO和∠PFO是直角,∴四边形PFOE是矩形,∴PF=OE,在Rt△PEO中,有PE2+OE2=PO2,∴PE2+PF2=PO2,即PE2+PF2=PO2成立;
④△BNF是等腰直角三角形,点P不在AB的中点时,△POF不是等腰直角三角形,所以△POF与△BNF不一定相似,即△POF∽△BNF不一定成立;
⑤∵△AMP是等腰直角三角形,△PMN∽△AMP,∴△PMN是等腰直角三角形,∵∠MPN=90°,∴PM=PN,∵AP=PM,BP=PN,∴AP=BP,∴点P是AB的中点,又∵O为正方形的对称中点,∴点O在M、N两点的连线上.综上,①②③⑤成立,即正确的结论有4个,答案选B.
二、填空题
9. 【答案】
【解析】由题意可知:构成三角形为等边三角形
10. 【答案】
【解析】根据菱形的性质可知:应当旋转至少
11. 【答案】或
12. 【答案】3
【解析】由于已知BC的长,故可设想在Rt△BCQ中利用勾股定理求解,则需求CQ的长,这可通过求DQ的长得到,结合已知条件BP=BA=5,易知DQ=DP,显然DP可求,思路沟通.
在矩形ABCD中,∠BAD=90?,AB=5,AD=12,∴BD==13,又∵BP=BA=5,∴DP=13-5=8,∠BAP=∠BPA.∵AB∥DQ,∴∠BAP=∠PQD,∴∠PQD=∠BPA=∠DPQ,∴DQ=DP=8,∴CQ=8-5=3.在Rt△BCQ中,BC=12,CQ=3,∴BQ==3.
13. 【答案】4.8 【解析】∵S菱形=AC·BD=2AB·DH,∴AC·BD=2AB·DH.∵四边形ABCD是菱形,∴∠AOB=90°,AO=AC=4,BO=BD=3,∴在Rt△AOB中,AB==5,∴DH==4.8.
14. 【答案】13 【解析】如解图,连接AC、BD交于O,则有AC·BD=120,∴AC·BD=240,又∵菱形对角线互相垂直平分,∴2OA·2OB=240,∴ OA·OB=60,∵AE2=50, OA2+OE2= AE2,OA=OE,∴OA=5,∴OB=12,∴AB===13.
解图
15. 【答案】或 【解析】如解图,过N作NG⊥AB,交AB于点G,∵四边形ABCD为正方形,∴AB=AD=NG= cm,在Rt△ABE中,∠BAE=30°,AB= cm,∴BE=1 cm,AE=2 cm,∵F为AE的中点,∴AF=AE=1 cm,在Rt△ABE和Rt△NGM中,,∴Rt△ABE≌Rt△NGM(HL),∴BE=GM,∠BAE=∠MNG=30°,∠AEB=∠NMG=60°,∴∠AFM=90°,即MN⊥AE,在Rt△AMF中,∠FAM=30°,AF=1 cm,∴AM=== cm,由对称性得到AM′=BM=AB-AM=-= cm,综上,AM的长等于或 cm.
解图
16. 【答案】
【解析】,则,所以得到
三、解答题
17. 【答案】
解:(1)证明:∵E是AD的中点,∴AE=DE,
又∵AF∥BC,
∴∠AFE=∠DBE,∠EAF=∠EDB,
∴△AEF≌△DEB.
(2)四边形ADCF是矩形.
证明:∵AF∥CD,AF=CD,
∴四边形ADCF是平行四边形.
∵△AEF≌△DEB,∴AF=BD,
∴BD=CD,即AD是△ABC的中线,
又∵AB=AC,∴AD⊥BC,
∴∠ADC=90°.
∴四边形ADCF是矩形.
18. 【答案】
∵四边形为平行四边形
∴,
∵、分别是、的平分线
∴
∴
同理
∴四边形是矩形.
