北师大版数学四年级下册5.3 方程 课件(15张ppt)
文档属性
| 名称 | 北师大版数学四年级下册5.3 方程 课件(15张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 05:41:48 | ||
图片预览





文档简介
第3课时 方程
五
认识方程
教学目标
1.在具体的情境中,会用含未知数的等式表示几个数量之间的关系,理解方程的含义。
2.在用方程表示简单的情境中的等量关系的过程中,感受方程与实际生活的密切关系。
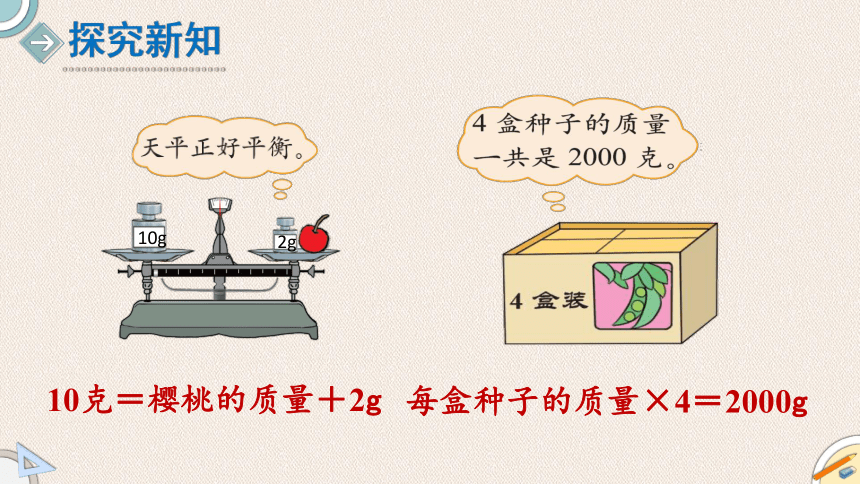
10g
2g
10克=樱桃的质量+2g
每盒种子的质量×4=2000g
2000毫升=每个热水瓶盛水量×2+200毫升
10g
2g
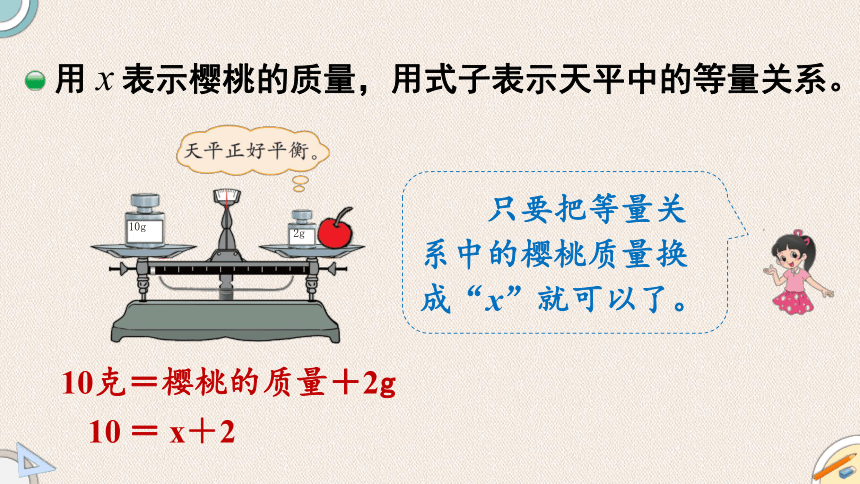
10克=樱桃的质量+2g
用 表示樱桃的质量,用式子表示天平中的等量关系。
10=x+2
只要把等量关系中的樱桃质量换成“x”就可以了。
每盒种子的质量×4=2000g
用y表示每盒种子的质量,用式子表示下面的等量关系。
4y=2000
这些等式有什么特点?与同伴进行交流。
像左边这样含有未知数的等式叫方程。
4y=2000
10=x+2
2000=2z+200
公元250年前后,古希腊数学家丢番图写了一本数学巨著《算术》,引入了未知数的概念,并使用符号表示未知数,这是数学史上的一个重要事件,开启了符号代数的大门。因此,人们常常称丢图番为“代数之父”。
1.先说一说各图中的等量关系,再列出方程。
(1)
x+20=70
(2)
5x +4=44
4x+6-3=87
(x-5)×4=2x
1. 先说一说各图中的等量关系,再列出方程。
(3)
2b+15=100
1. 先说一说各图中的等量关系,再列出方程。
(4)
2. 根据题意先说出等量关系再列出方程。
⑴一辆公共汽车到站时,有5人下车,8人上车,车
上现有15人,车上原有x人,那么 。
⑵用95个小正方形摆出了x个大门,那么 。
x-5+8=15
5x=95
3. 日历表的规律。
认真观察下图阴影方框中正中间的数与其
他四个数的关系。
⑴中间数是y,左边的数是 ,右边
的数是 ,上面的数是 ,下面
的数是 。
⑵方框中5个数之和与中间的数有什么关系?
⑶当5个数的和是115时,中间的数是多少?
5个数之和是中间数的倍数。
23
y?1
y+1
y?7
y+7
含有未知数的等式叫方程。例:
4x=12 3x?4=11
五
认识方程
教学目标
1.在具体的情境中,会用含未知数的等式表示几个数量之间的关系,理解方程的含义。
2.在用方程表示简单的情境中的等量关系的过程中,感受方程与实际生活的密切关系。
10g
2g
10克=樱桃的质量+2g
每盒种子的质量×4=2000g
2000毫升=每个热水瓶盛水量×2+200毫升
10g
2g
10克=樱桃的质量+2g
用 表示樱桃的质量,用式子表示天平中的等量关系。
10=x+2
只要把等量关系中的樱桃质量换成“x”就可以了。
每盒种子的质量×4=2000g
用y表示每盒种子的质量,用式子表示下面的等量关系。
4y=2000
这些等式有什么特点?与同伴进行交流。
像左边这样含有未知数的等式叫方程。
4y=2000
10=x+2
2000=2z+200
公元250年前后,古希腊数学家丢番图写了一本数学巨著《算术》,引入了未知数的概念,并使用符号表示未知数,这是数学史上的一个重要事件,开启了符号代数的大门。因此,人们常常称丢图番为“代数之父”。
1.先说一说各图中的等量关系,再列出方程。
(1)
x+20=70
(2)
5x +4=44
4x+6-3=87
(x-5)×4=2x
1. 先说一说各图中的等量关系,再列出方程。
(3)
2b+15=100
1. 先说一说各图中的等量关系,再列出方程。
(4)
2. 根据题意先说出等量关系再列出方程。
⑴一辆公共汽车到站时,有5人下车,8人上车,车
上现有15人,车上原有x人,那么 。
⑵用95个小正方形摆出了x个大门,那么 。
x-5+8=15
5x=95
3. 日历表的规律。
认真观察下图阴影方框中正中间的数与其
他四个数的关系。
⑴中间数是y,左边的数是 ,右边
的数是 ,上面的数是 ,下面
的数是 。
⑵方框中5个数之和与中间的数有什么关系?
⑶当5个数的和是115时,中间的数是多少?
5个数之和是中间数的倍数。
23
y?1
y+1
y?7
y+7
含有未知数的等式叫方程。例:
4x=12 3x?4=11
