北师大版数学四年级下册5.5 解方程(二) 课件(共16张PPT)
文档属性
| 名称 | 北师大版数学四年级下册5.5 解方程(二) 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 05:50:56 | ||
图片预览


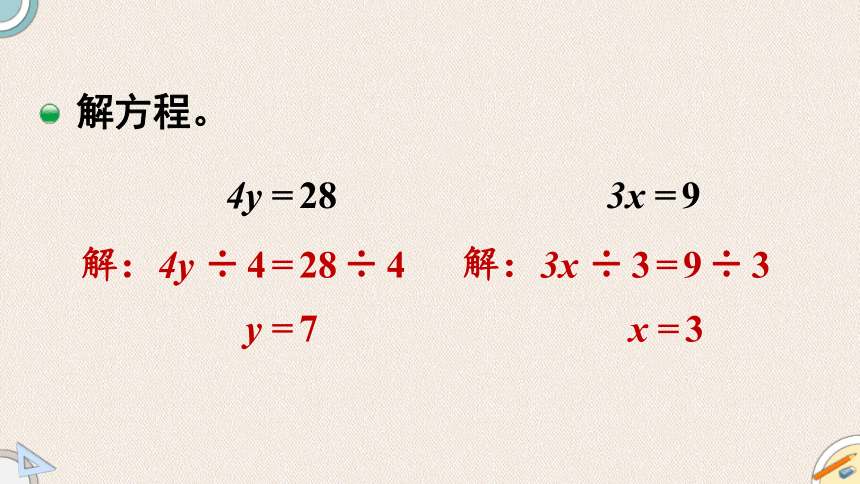
文档简介
第5课时 解方程(二)
五
认识方程
教学目标
1.借助天平平衡的原理,探索等式两边都乘同一个数或除以同一个不为0的数,等式仍然成立的性质。
2.结合小数乘整数的意义,能够正确地计算简单的小数乘整数。
5g
g
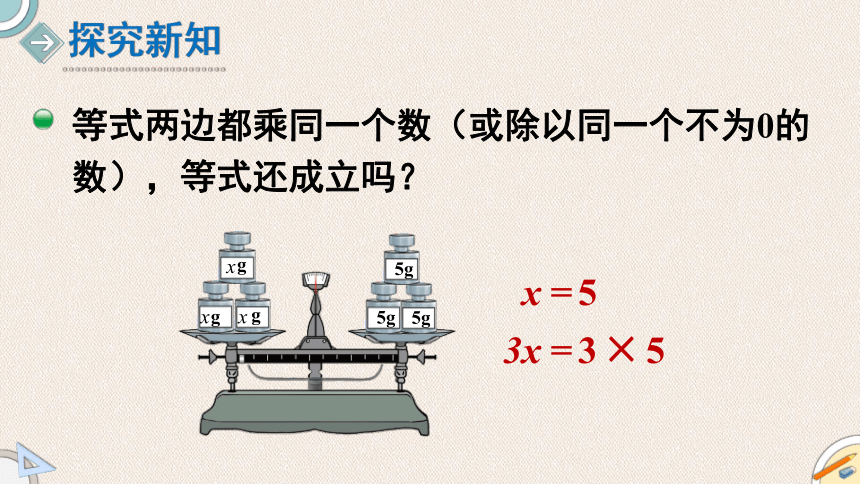
x =5
5g
g
5g
g
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
3x =3×5
10g
10g
g
g
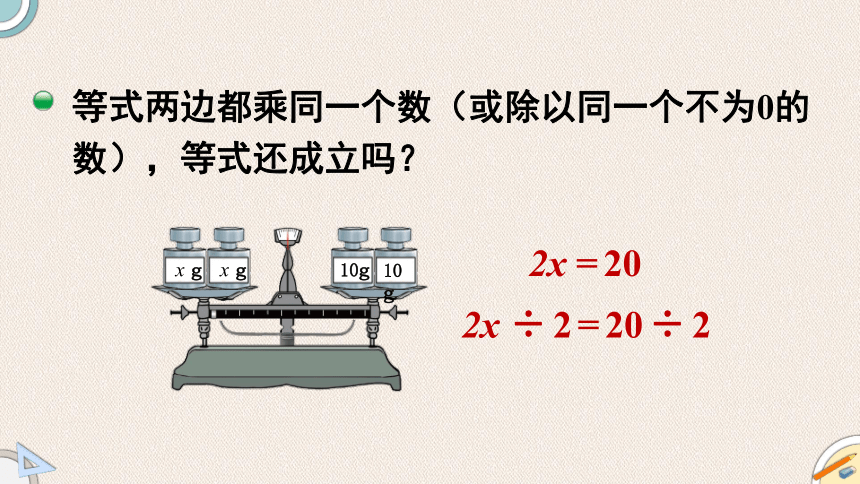
2x =20
2x ÷2=20÷2
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
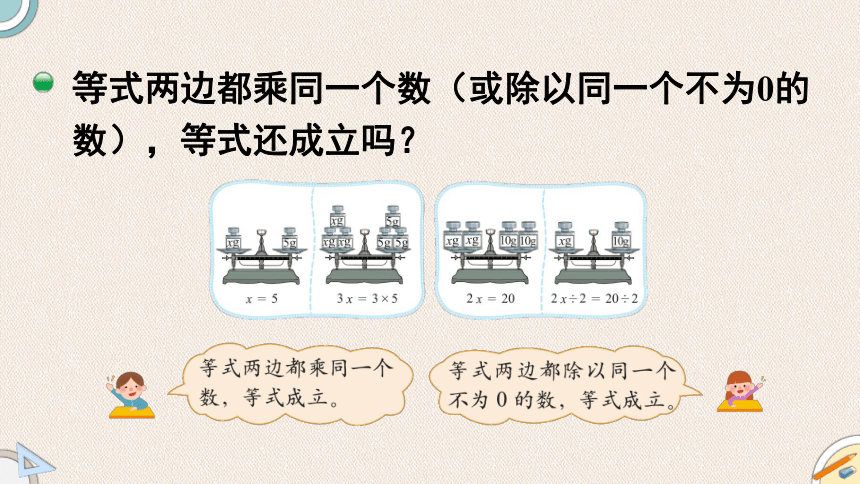
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
解:
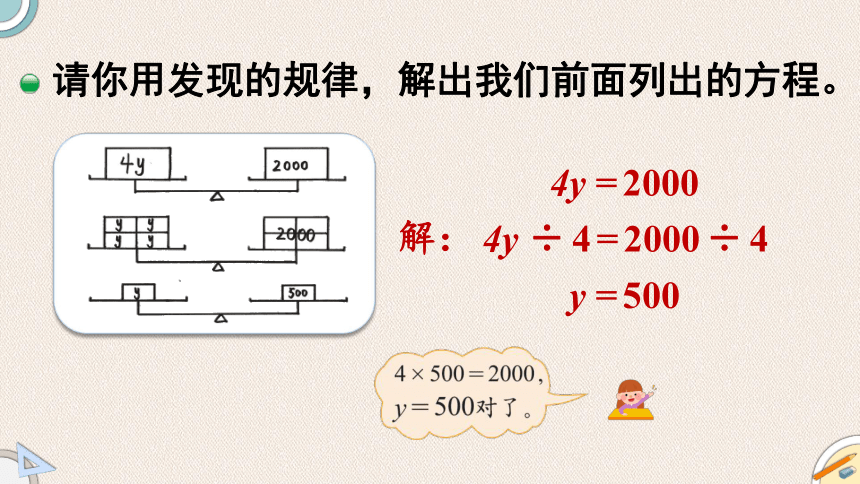
请你用发现的规律,解出我们前面列出的方程。
4y =2000
4y ÷4=2000÷4
y =500
解方程。
解:
4y =28
4y ÷4=28÷4
y =7
解:
3x =9
3x ÷3=9÷3
x =3
38
等号两边要相等哦。
下面解法正确吗?与同伴交流。
1. 请你画图或举例说说下面这句话的意思:等式
两边都乘同一个数(或除以同一个不为0的数),
等式仍然成立。
例: x=10
4x=4×10
x÷2=10÷2
2. 森林医生。
7x =35=35÷7=5
-5=8
解:
-5 =8
= 3
-5
-5
+5
+5
=13
解:
7x =35
7x ÷7=35÷7
x =5
3. 解方程。
解:
x÷3 =9
x ÷3×3=9×3
x =27
解:
7y =28
7y ÷7=28÷7
y =4
4. 长方形游泳池占地600米2,长30米,游泳池宽
多少米?
30x=600
x=20
解:设游泳池宽x米。
答:游泳池宽20米。
5. 某地为便于残疾人轮椅通行,通
过了一项关于建筑物前斜坡高度
的规定:每1米高的斜坡,至少
需要12米的水平长度。
⑴ 2米高的斜坡,至少需要多少米的水平长度?4米、
x米高呢?
24米,48米,x米高的斜坡,至少需要12x米的水平高度。
⑵ 某建筑物前的空地长36米,那么此处斜坡最高多
少米?
解:设设斜坡最高为x米。
12x=36
x=3
答:此处斜坡最高为3米。
5. 某地为便于残疾人轮椅通行,通
过了一项关于建筑物前斜坡高度
的规定:每1米高的斜坡,至少
需要12米的水平长度。
等式的性质2:等式两边都乘同一个数或除以同一个不为0的数,等式仍然成立。
解形如“ax=b”“x÷a=b”(a不为0)的方程时,可以根据等式的性质2,在方程两边同时除以a或乘a,使方程的左边只剩下未知数x,这时方程右边的数b÷a或ab就是x的值。
五
认识方程
教学目标
1.借助天平平衡的原理,探索等式两边都乘同一个数或除以同一个不为0的数,等式仍然成立的性质。
2.结合小数乘整数的意义,能够正确地计算简单的小数乘整数。
5g
g
x =5
5g
g
5g
g
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
3x =3×5
10g
10g
g
g
2x =20
2x ÷2=20÷2
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
等式两边都乘同一个数(或除以同一个不为0的数),等式还成立吗?
解:
请你用发现的规律,解出我们前面列出的方程。
4y =2000
4y ÷4=2000÷4
y =500
解方程。
解:
4y =28
4y ÷4=28÷4
y =7
解:
3x =9
3x ÷3=9÷3
x =3
38
等号两边要相等哦。
下面解法正确吗?与同伴交流。
1. 请你画图或举例说说下面这句话的意思:等式
两边都乘同一个数(或除以同一个不为0的数),
等式仍然成立。
例: x=10
4x=4×10
x÷2=10÷2
2. 森林医生。
7x =35=35÷7=5
-5=8
解:
-5 =8
= 3
-5
-5
+5
+5
=13
解:
7x =35
7x ÷7=35÷7
x =5
3. 解方程。
解:
x÷3 =9
x ÷3×3=9×3
x =27
解:
7y =28
7y ÷7=28÷7
y =4
4. 长方形游泳池占地600米2,长30米,游泳池宽
多少米?
30x=600
x=20
解:设游泳池宽x米。
答:游泳池宽20米。
5. 某地为便于残疾人轮椅通行,通
过了一项关于建筑物前斜坡高度
的规定:每1米高的斜坡,至少
需要12米的水平长度。
⑴ 2米高的斜坡,至少需要多少米的水平长度?4米、
x米高呢?
24米,48米,x米高的斜坡,至少需要12x米的水平高度。
⑵ 某建筑物前的空地长36米,那么此处斜坡最高多
少米?
解:设设斜坡最高为x米。
12x=36
x=3
答:此处斜坡最高为3米。
5. 某地为便于残疾人轮椅通行,通
过了一项关于建筑物前斜坡高度
的规定:每1米高的斜坡,至少
需要12米的水平长度。
等式的性质2:等式两边都乘同一个数或除以同一个不为0的数,等式仍然成立。
解形如“ax=b”“x÷a=b”(a不为0)的方程时,可以根据等式的性质2,在方程两边同时除以a或乘a,使方程的左边只剩下未知数x,这时方程右边的数b÷a或ab就是x的值。
