北师大版 九年级下册数学 3.3垂径定理 同步测试(Word版 含解析)
文档属性
| 名称 | 北师大版 九年级下册数学 3.3垂径定理 同步测试(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 221.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 10:18:09 | ||
图片预览




文档简介
3.3垂径定理
同步测试
一.选择题
1.如图,AB为⊙O的直径,点C在⊙O上,若AB=4,,则O到AC的距离为( )
A.1
B.2
C.
D.
2.如图,AB,BC是⊙O的两条弦,AO⊥BC,垂足为D,若⊙O的直径为5,BC=4,则AB的长为( )
A.2
B.2
C.4
D.5
3.如图,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB的延长线上一点,BP=2cm,则OP等于( )
A.cm
B.3
cm
C.cm
D.cm
4.半径为5的圆内有长为的弦,则此弦所对的圆周角为( )
A.60°
B.120°
C.60°或120°
D.30°或120°
5.如图,在平面直角坐标系中,⊙P的圆心坐标是(﹣3,a)(a>3),半径为3,函数y=﹣x的图象被⊙P截得的弦AB的长为,则a的值是( )
A.4
B.
C.
D.
6.图中的三块阴影部分由两个半径为1的圆及其外公切线分割而成,如果中间一块阴影的面积等于上下两块面积之和,则这两圆的公共弦长是( )
A.
B.
C.
D.
7.已知圆O的半径为5,P是圆O内一点,且OP=3,过点P作圆O的一条弦AB,则AB值不可以是( )
A.7
B.8
C.9
D.10
8.如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
A.4个
B.5个
C.6个
D.7个
9.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EB.若AB=4,CD=1,则EB的长为( )
A.3
B.4
C.5
D.2.5
10.如图,以M(4,0)为圆心,3为半径的圆与x轴交于点A、B,P是⊙M上异于A、B的一动点,直线PA与PB分别交y轴于点C、D,以CD为直径的⊙N交x轴于点E、F,则EF的长( )
A.2
B.5
C.2
D.不能确定
二.填空题
11.直线l:m(2x﹣y﹣5)+(3x﹣8y﹣14)=0被以点A(1,0)为圆心,2为半径的⊙A所截得的最短弦的长为
.
12.在△ABC中,AB=AC=5,sinB=,⊙O过点B、C两点,且⊙O半径r=,则OA的长为
.
13.如图,已知⊙O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP=
.
14.某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,则这个圆形截面的半径为
cm.
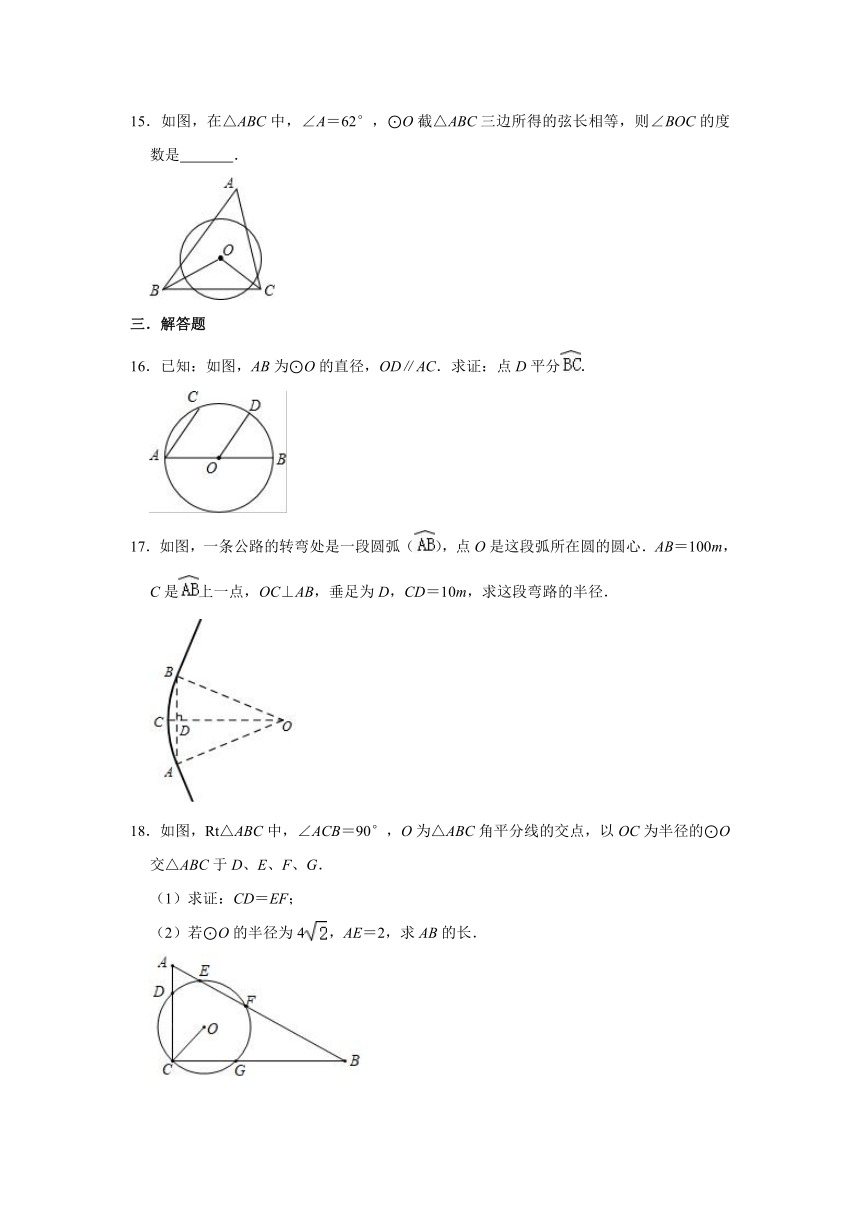
15.如图,在△ABC中,∠A=62°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是
.
三.解答题
16.已知:如图,AB为⊙O的直径,OD∥AC.求证:点D平分.
17.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心.AB=100m,C是上一点,OC⊥AB,垂足为D,CD=10m,求这段弯路的半径.
18.如图,Rt△ABC中,∠ACB=90°,O为△ABC角平分线的交点,以OC为半径的⊙O交△ABC于D、E、F、G.
(1)求证:CD=EF;
(2)若⊙O的半径为4,AE=2,求AB的长.
参考答案
一.选择题
1.解:连接BC,作OE⊥AC于E.
∵AB是直径,
∴∠ACB=90°,
∴BC===2,
∵OE⊥AC,
∴AE=EC,
∵AO=OB,
∴OE=BC=,
故选:C.
2.解:连接OB,
∵AO⊥BC,AO过O,BC=4,
∴BD=CD=2,∠BDO=90°,
由勾股定理得:OD===,
∴AD=OA+OD=+=4,
在Rt△ADB中,由勾股定理得:AB===2,
故选:A.
3.解:过O作OC⊥AB于C,
则∠OCP=∠ACO=90°,
∵OC⊥AB,OC过O,
∴AC=BC=AB=×8cm=4cm,
∵BP=2cm,
∴PC=BC+BP=6cm,
在Rt△ACO中,由勾股定理得:OC===3(cm),
在Rt△PCO中,由勾股定理得:OP===3(cm),
故选:D.
4.解:如图所示,
∵OD⊥AB,
∴D为AB的中点,即AD=BD=,
在Rt△AOD中,OA=5,AD=,
∴sin∠AOD==,
又∵∠AOD为锐角,
∴∠AOD=60°,
∴∠AOB=120°,
∴∠ACB=∠AOB=60°,
又∵圆内接四边形AEBC对角互补,
∴∠AEB=120°,
则此弦所对的圆周角为60°或120°.
故选:C.
5.解:过P作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连接PB,如图:
∵⊙P的圆心坐标是(﹣3,a),
∴OC=3,PC=a,
把x=3代入y=﹣x得:y=﹣3,
∴D点坐标为(3,﹣3),
∴CD=OC=3,
∴△OCD为等腰直角三角形,
∴∠CDO=45°,
∵PE⊥AB,
∴△PED为等腰直角三角形,AE=BE=AB=×4=2,
在Rt△PBE中,PB=3,
∴PE==1,
∴PD=PE=,
∴PC=CD+PD=3+,
即a=3+,
故选:B.
6.解:∵AB,CD为两等圆的公切线,
∴四边形ABCD为矩形,BC=2,
设中间一块阴影的面积为S,
∵中间一块阴影的面积等于上下两块面积之和,
∴BC?AB﹣(S半圆AD+S半圆BC﹣S)=S,即2AB﹣π?12+S=S,
∴AB=.
如图,EF为公共弦,PO⊥EF,
OP=AB=,
∴EP===,
∴EF=2EP=.
故选:D.
7.解:过点P作CD⊥OP,⊙O于C,D.连接OC.
∵OC=5,OP=3,∠OPC=90°,
∴PC===4,
∵OP⊥CD,
∴PC=PD=4,
∴CD=8,
∴过点P的最短的弦长为8,最长的弦长为10,
故选:A.
8.解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=16,∴AP=BP=8,
在直角三角形AOP中,OA=10,AP=8,
根据勾股定理得:OP===6,即OP的最小值为6;
当P与A或B重合时,OP最长,此时OP=10,
∴6≤OP<10,
则使线段OP的长度为整数,
∴OP=6,7,8,9.
根据对称性可知,满足条件的点P的个数有7个
故选:D.
9.解:设⊙O的半径为r.
∵OD⊥AB,
∴AC=BC=2,
在Rt△AOC中,∵∠ACO=90°,
∴OA2=OC2+AC2,
∴r2=(r﹣1)2+22,
∴r=,
∴OC=,
∵OA=OE,AC=CB,
∴BE=2OC=3,
故选:A.
10.解:∵M(4,0),AB=6,
∴AM=BM=3,
∴OA=1,
∵CD⊥EF,
∴OE=OF,设OE=OF=x,
∵∠COA=∠APB=90°,
∴C,O,P,B四点共圆,
∴AP?AC=AO?AB,
∵AE?AF=AC?PA,
∴AE?AF=OA?AB,
∴(x+1)(x﹣1)=1×6,
∴x2=7,
∴x=,
∴EF=2OE=2,
故选:A.
二.填空题
11.解:解方程组,
解得:,
则直线l一定经过点B(2,﹣1).
AB=<2,
∴B一定在⊙A的内部,当直线l与AB垂直时,直线l截得⊙A所得的弦最短,
∴最短的弦长是:2=2.
故答案为:2.
12.解:如图,作AD⊥BC于D,
∵AB=AC=5,
∴AD垂直平分BC,
∴点O在直线AD上,
连结OB,
在Rt△ABD中,sinB==,
∵AB=5,
∴AD=4,
∴BD===3,
在Rt△OBD中,OB=,BD=3,
∴OD==1,
当点A与点O在BC的两侧时,OA=AD+OD=4+1=5;
当点A与点O在BC的同侧时,OA=AD﹣OD=4﹣1=3,
故OA的长为3或5.
故答案为3或5.
13.解:作OE⊥AB交AB与点E,作OF⊥CD交CD于点F,连接OB、OD,如右图所示,
则AE=BE,CF=DF,∠OFP=∠OEP=90°,
又∵圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,
∴∠FPE=90°,OB=10,BE=8,
∴四边形OEPF是矩形,OE=6,
同理可得,OF=6,
∴EP=OF=6,
∴OP==6,
故答案为:6.
14.解:设此圆形截面所在圆的圆心为O,连接OA,过点O作OD⊥AB于点D,交弧于点C,
则CD=4cm,AD=AB=×16=8(cm),
设这个圆形截面的半径为rcm,
则OD=OC﹣CD=r﹣4(cm)
∵在Rt△AOD中,OA2=OD2+AD2,
∴r2=(r﹣4)2+82,
解得:r=10,
故这个圆形截面的半径为10cm.
故答案为:10.
15.解:∵△ABC中∠A=62°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣62°)=59°,
∴∠BOC=180°﹣(∠1+∠3)=180°﹣59°=121°.
故答案是:121°.
三.解答题
16.证明:连接CB,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵OD∥AC,
∴∠OEB=∠ACB=90°,
即OD⊥BC,
∵OD过O,
∴点D平分.
17.解:设这段弯路的半径为r
m,
∵OC⊥AB于D,AB=100(m),
∴BD=DA=AB=50(m)
∵CD=10(m),
得OD=r﹣10(m).
∵Rt△BOD中,根据勾股定理有BO2=BD2+DO2
即r2=502+(r﹣10)2
解得r=130(m).
答:这段弯路的半径为130
m.
18.(1)证明:作OM⊥AB于M,ON⊥AC于N,OH⊥CG于G,连接OE、OD,
∵点O为△ABC的角平分线交点,
∴OM=ON,
∵OE=OD=OC,
∴RT△OME≌RT△OND(HL),
∴ME=ND,
∵EF=2ME,CD=2ND,
∴CD=EF;
(2)解:由(1)可知CD=EF=CG,
∵点O为△ABC的角平分线交点,
∴OM=ON=OH,
∵∠ACB=90°,
∴四边形ONCH是正方形,
∴OM=ON=OH=CD=EF=CG,
∵OC=4,
∴OH=OC=4,
∴EF=CD=CG=8,
易证得AM=AN=6,BM=BH,
∴AC=10,
设BM=BH=x,则BC=x+4,AB=x+6,
∵∠ACB=90°,
∴AB2=AC2+BC2,即(6+x)2=102+(4+x)2,
解得x=20,
∴BM=20,
∴AB=AM+BM=20+6=26.
同步测试
一.选择题
1.如图,AB为⊙O的直径,点C在⊙O上,若AB=4,,则O到AC的距离为( )
A.1
B.2
C.
D.
2.如图,AB,BC是⊙O的两条弦,AO⊥BC,垂足为D,若⊙O的直径为5,BC=4,则AB的长为( )
A.2
B.2
C.4
D.5
3.如图,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB的延长线上一点,BP=2cm,则OP等于( )
A.cm
B.3
cm
C.cm
D.cm
4.半径为5的圆内有长为的弦,则此弦所对的圆周角为( )
A.60°
B.120°
C.60°或120°
D.30°或120°
5.如图,在平面直角坐标系中,⊙P的圆心坐标是(﹣3,a)(a>3),半径为3,函数y=﹣x的图象被⊙P截得的弦AB的长为,则a的值是( )
A.4
B.
C.
D.
6.图中的三块阴影部分由两个半径为1的圆及其外公切线分割而成,如果中间一块阴影的面积等于上下两块面积之和,则这两圆的公共弦长是( )
A.
B.
C.
D.
7.已知圆O的半径为5,P是圆O内一点,且OP=3,过点P作圆O的一条弦AB,则AB值不可以是( )
A.7
B.8
C.9
D.10
8.如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
A.4个
B.5个
C.6个
D.7个
9.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EB.若AB=4,CD=1,则EB的长为( )
A.3
B.4
C.5
D.2.5
10.如图,以M(4,0)为圆心,3为半径的圆与x轴交于点A、B,P是⊙M上异于A、B的一动点,直线PA与PB分别交y轴于点C、D,以CD为直径的⊙N交x轴于点E、F,则EF的长( )
A.2
B.5
C.2
D.不能确定
二.填空题
11.直线l:m(2x﹣y﹣5)+(3x﹣8y﹣14)=0被以点A(1,0)为圆心,2为半径的⊙A所截得的最短弦的长为
.
12.在△ABC中,AB=AC=5,sinB=,⊙O过点B、C两点,且⊙O半径r=,则OA的长为
.
13.如图,已知⊙O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP=
.
14.某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,则这个圆形截面的半径为
cm.
15.如图,在△ABC中,∠A=62°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是
.
三.解答题
16.已知:如图,AB为⊙O的直径,OD∥AC.求证:点D平分.
17.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心.AB=100m,C是上一点,OC⊥AB,垂足为D,CD=10m,求这段弯路的半径.
18.如图,Rt△ABC中,∠ACB=90°,O为△ABC角平分线的交点,以OC为半径的⊙O交△ABC于D、E、F、G.
(1)求证:CD=EF;
(2)若⊙O的半径为4,AE=2,求AB的长.
参考答案
一.选择题
1.解:连接BC,作OE⊥AC于E.
∵AB是直径,
∴∠ACB=90°,
∴BC===2,
∵OE⊥AC,
∴AE=EC,
∵AO=OB,
∴OE=BC=,
故选:C.
2.解:连接OB,
∵AO⊥BC,AO过O,BC=4,
∴BD=CD=2,∠BDO=90°,
由勾股定理得:OD===,
∴AD=OA+OD=+=4,
在Rt△ADB中,由勾股定理得:AB===2,
故选:A.
3.解:过O作OC⊥AB于C,
则∠OCP=∠ACO=90°,
∵OC⊥AB,OC过O,
∴AC=BC=AB=×8cm=4cm,
∵BP=2cm,
∴PC=BC+BP=6cm,
在Rt△ACO中,由勾股定理得:OC===3(cm),
在Rt△PCO中,由勾股定理得:OP===3(cm),
故选:D.
4.解:如图所示,
∵OD⊥AB,
∴D为AB的中点,即AD=BD=,
在Rt△AOD中,OA=5,AD=,
∴sin∠AOD==,
又∵∠AOD为锐角,
∴∠AOD=60°,
∴∠AOB=120°,
∴∠ACB=∠AOB=60°,
又∵圆内接四边形AEBC对角互补,
∴∠AEB=120°,
则此弦所对的圆周角为60°或120°.
故选:C.
5.解:过P作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连接PB,如图:
∵⊙P的圆心坐标是(﹣3,a),
∴OC=3,PC=a,
把x=3代入y=﹣x得:y=﹣3,
∴D点坐标为(3,﹣3),
∴CD=OC=3,
∴△OCD为等腰直角三角形,
∴∠CDO=45°,
∵PE⊥AB,
∴△PED为等腰直角三角形,AE=BE=AB=×4=2,
在Rt△PBE中,PB=3,
∴PE==1,
∴PD=PE=,
∴PC=CD+PD=3+,
即a=3+,
故选:B.
6.解:∵AB,CD为两等圆的公切线,
∴四边形ABCD为矩形,BC=2,
设中间一块阴影的面积为S,
∵中间一块阴影的面积等于上下两块面积之和,
∴BC?AB﹣(S半圆AD+S半圆BC﹣S)=S,即2AB﹣π?12+S=S,
∴AB=.
如图,EF为公共弦,PO⊥EF,
OP=AB=,
∴EP===,
∴EF=2EP=.
故选:D.
7.解:过点P作CD⊥OP,⊙O于C,D.连接OC.
∵OC=5,OP=3,∠OPC=90°,
∴PC===4,
∵OP⊥CD,
∴PC=PD=4,
∴CD=8,
∴过点P的最短的弦长为8,最长的弦长为10,
故选:A.
8.解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=16,∴AP=BP=8,
在直角三角形AOP中,OA=10,AP=8,
根据勾股定理得:OP===6,即OP的最小值为6;
当P与A或B重合时,OP最长,此时OP=10,
∴6≤OP<10,
则使线段OP的长度为整数,
∴OP=6,7,8,9.
根据对称性可知,满足条件的点P的个数有7个
故选:D.
9.解:设⊙O的半径为r.
∵OD⊥AB,
∴AC=BC=2,
在Rt△AOC中,∵∠ACO=90°,
∴OA2=OC2+AC2,
∴r2=(r﹣1)2+22,
∴r=,
∴OC=,
∵OA=OE,AC=CB,
∴BE=2OC=3,
故选:A.
10.解:∵M(4,0),AB=6,
∴AM=BM=3,
∴OA=1,
∵CD⊥EF,
∴OE=OF,设OE=OF=x,
∵∠COA=∠APB=90°,
∴C,O,P,B四点共圆,
∴AP?AC=AO?AB,
∵AE?AF=AC?PA,
∴AE?AF=OA?AB,
∴(x+1)(x﹣1)=1×6,
∴x2=7,
∴x=,
∴EF=2OE=2,
故选:A.
二.填空题
11.解:解方程组,
解得:,
则直线l一定经过点B(2,﹣1).
AB=<2,
∴B一定在⊙A的内部,当直线l与AB垂直时,直线l截得⊙A所得的弦最短,
∴最短的弦长是:2=2.
故答案为:2.
12.解:如图,作AD⊥BC于D,
∵AB=AC=5,
∴AD垂直平分BC,
∴点O在直线AD上,
连结OB,
在Rt△ABD中,sinB==,
∵AB=5,
∴AD=4,
∴BD===3,
在Rt△OBD中,OB=,BD=3,
∴OD==1,
当点A与点O在BC的两侧时,OA=AD+OD=4+1=5;
当点A与点O在BC的同侧时,OA=AD﹣OD=4﹣1=3,
故OA的长为3或5.
故答案为3或5.
13.解:作OE⊥AB交AB与点E,作OF⊥CD交CD于点F,连接OB、OD,如右图所示,
则AE=BE,CF=DF,∠OFP=∠OEP=90°,
又∵圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,
∴∠FPE=90°,OB=10,BE=8,
∴四边形OEPF是矩形,OE=6,
同理可得,OF=6,
∴EP=OF=6,
∴OP==6,
故答案为:6.
14.解:设此圆形截面所在圆的圆心为O,连接OA,过点O作OD⊥AB于点D,交弧于点C,
则CD=4cm,AD=AB=×16=8(cm),
设这个圆形截面的半径为rcm,
则OD=OC﹣CD=r﹣4(cm)
∵在Rt△AOD中,OA2=OD2+AD2,
∴r2=(r﹣4)2+82,
解得:r=10,
故这个圆形截面的半径为10cm.
故答案为:10.
15.解:∵△ABC中∠A=62°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣62°)=59°,
∴∠BOC=180°﹣(∠1+∠3)=180°﹣59°=121°.
故答案是:121°.
三.解答题
16.证明:连接CB,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵OD∥AC,
∴∠OEB=∠ACB=90°,
即OD⊥BC,
∵OD过O,
∴点D平分.
17.解:设这段弯路的半径为r
m,
∵OC⊥AB于D,AB=100(m),
∴BD=DA=AB=50(m)
∵CD=10(m),
得OD=r﹣10(m).
∵Rt△BOD中,根据勾股定理有BO2=BD2+DO2
即r2=502+(r﹣10)2
解得r=130(m).
答:这段弯路的半径为130
m.
18.(1)证明:作OM⊥AB于M,ON⊥AC于N,OH⊥CG于G,连接OE、OD,
∵点O为△ABC的角平分线交点,
∴OM=ON,
∵OE=OD=OC,
∴RT△OME≌RT△OND(HL),
∴ME=ND,
∵EF=2ME,CD=2ND,
∴CD=EF;
(2)解:由(1)可知CD=EF=CG,
∵点O为△ABC的角平分线交点,
∴OM=ON=OH,
∵∠ACB=90°,
∴四边形ONCH是正方形,
∴OM=ON=OH=CD=EF=CG,
∵OC=4,
∴OH=OC=4,
∴EF=CD=CG=8,
易证得AM=AN=6,BM=BH,
∴AC=10,
设BM=BH=x,则BC=x+4,AB=x+6,
∵∠ACB=90°,
∴AB2=AC2+BC2,即(6+x)2=102+(4+x)2,
解得x=20,
∴BM=20,
∴AB=AM+BM=20+6=26.
