人教高中数学选修1-2:3.1数系的扩充与复数的概念 课件(34张ppt)
文档属性
| 名称 | 人教高中数学选修1-2:3.1数系的扩充与复数的概念 课件(34张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 17:42:58 | ||
图片预览




文档简介
(共37张PPT)
毕达哥拉斯(约公元前560—480年)
“数”是万物的本源,支配整个自然界和人类社会.世间一切事物都可归结为数或数的比例,这是世界所以美好和谐的源泉.
计数的需要
正整数
零
自然数
SHUXI
DI
KUOCHONG
数系的扩充
SHUXI
DI
KUOCHONG
数系的扩充
中国是世界上最早认识应用负数的
国家.早在2000多年前的《九章算术》
中,就有正数和负数的记载.在古代人民
生活中,以收入钱为正,以支出钱为负.在
粮食生产中,以产量增加为正,以产量减
少为负.古代的人们为区别正、负数,常
用红色算筹表示正,黑色算筹表示负.
小贴士
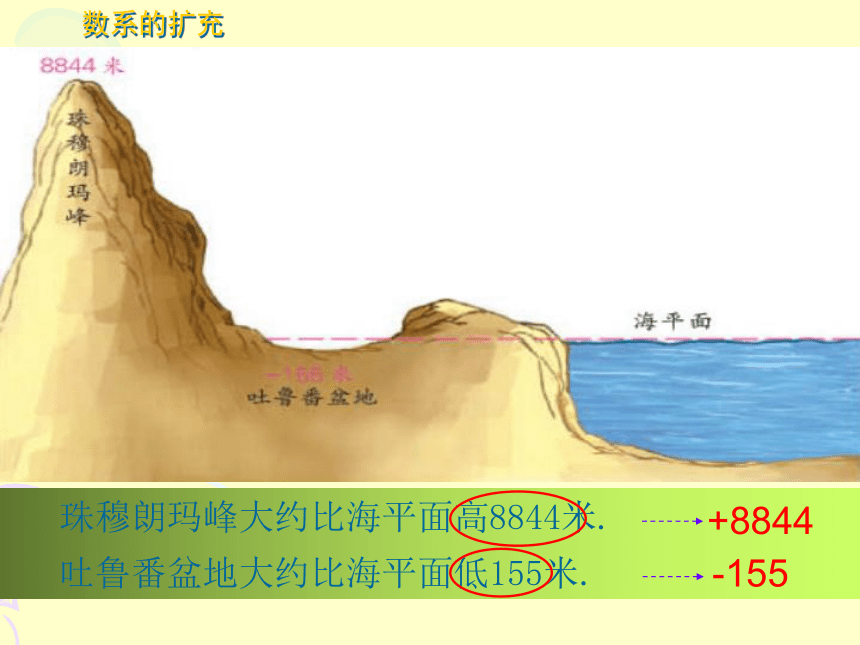
珠穆朗玛峰大约比海平面高8844米.
吐鲁番盆地大约比海平面低155米.
+8844
-155
SHUXI
DI
KUOCHONG
数系的扩充
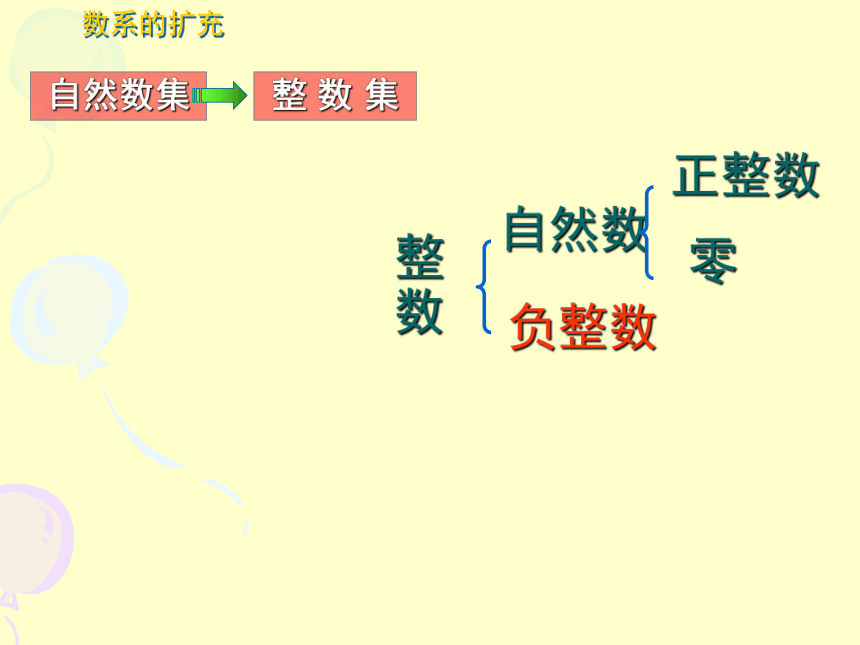
自然数集
整数
负整数
自然数
正整数
零
整
数
集
SHUXI
DI
KUOCHONG
数系的扩充
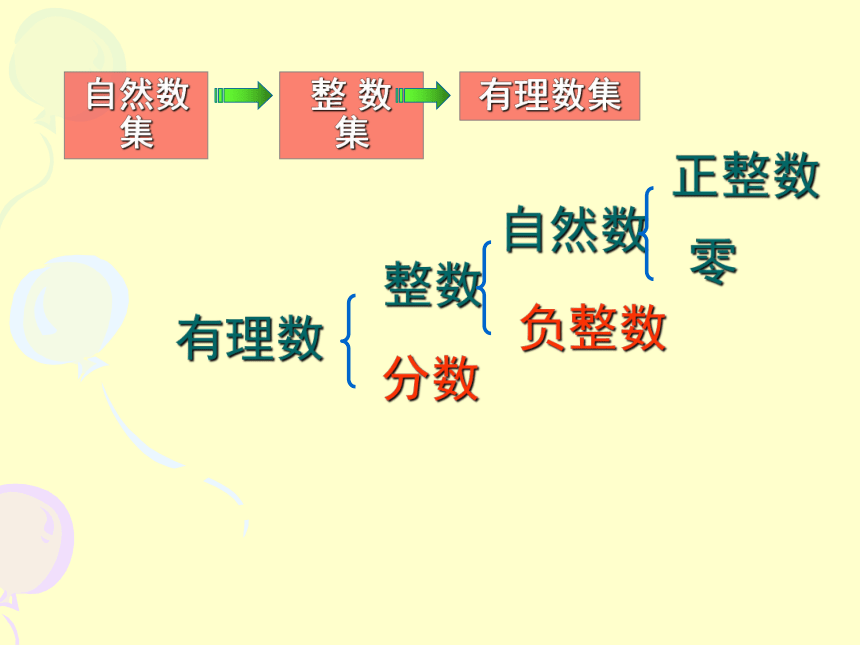
整数
负整数
自然数
正整数
零
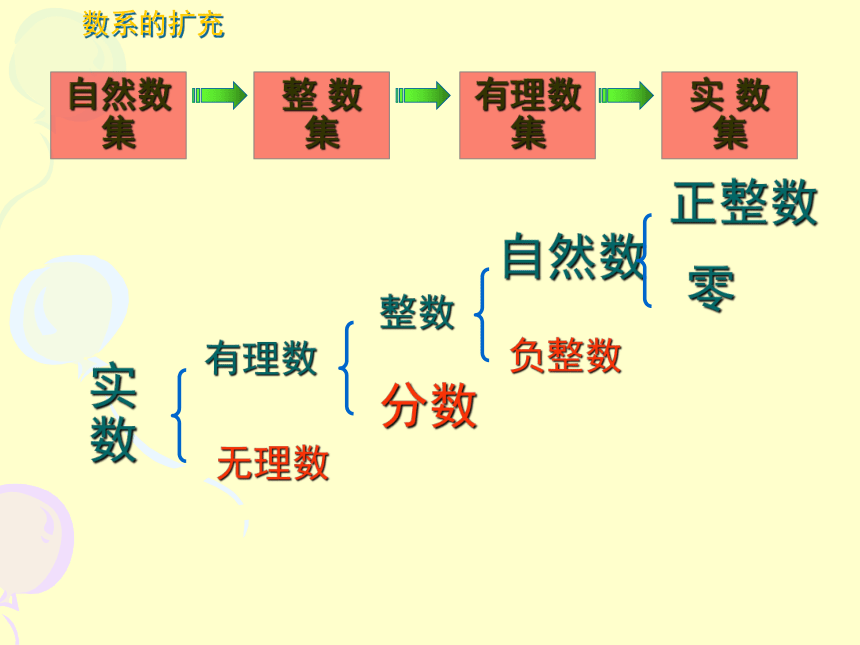
分数
有理数
有理数集
自然数集
整
数
集
1
1
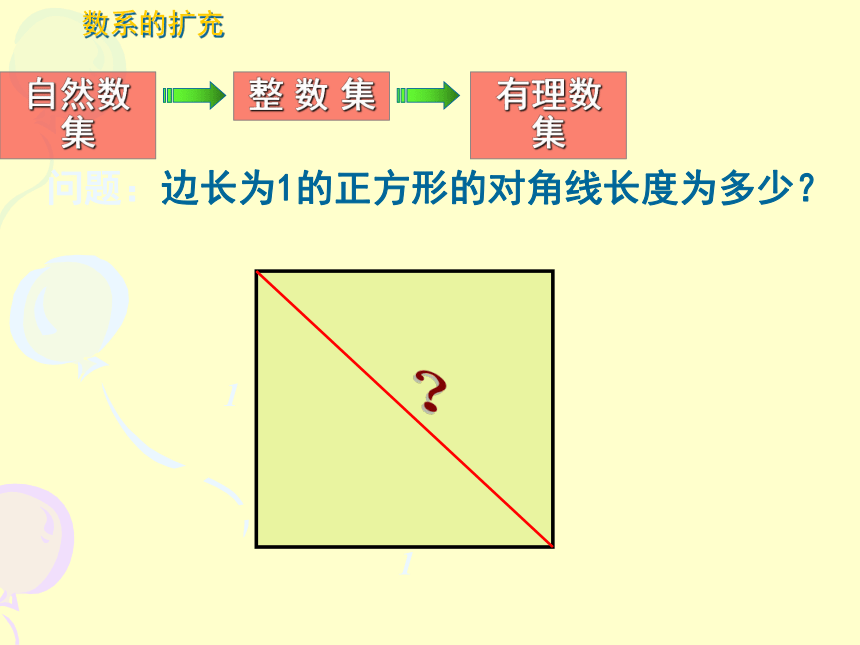
问题:边长为1的正方形的对角线长度为多少?
SHUXI
DI
KUOCHONG
数系的扩充
有理数集
自然数集
整
数
集
整数
负整数
自然数
正整数
零
分数
有理数
无理数
实数
实
数
集
SHUXI
DI
KUOCHONG
数系的扩充
有理数集
自然数集
整
数
集
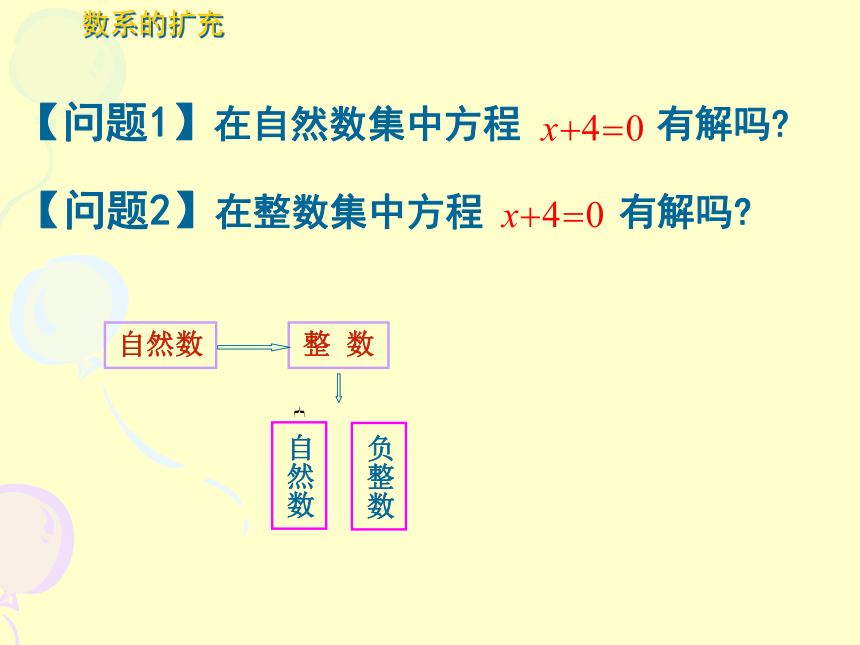
【问题1】在自然数集中方程
有解吗?
【问题2】在整数集中方程
有解吗?
自然数
整
数
自然数
负整数
SHUXI
DI
KUOCHONG
数系的扩充
有理数
整数
分数
SHUXI
DI
KUOCHONG
数系的扩充
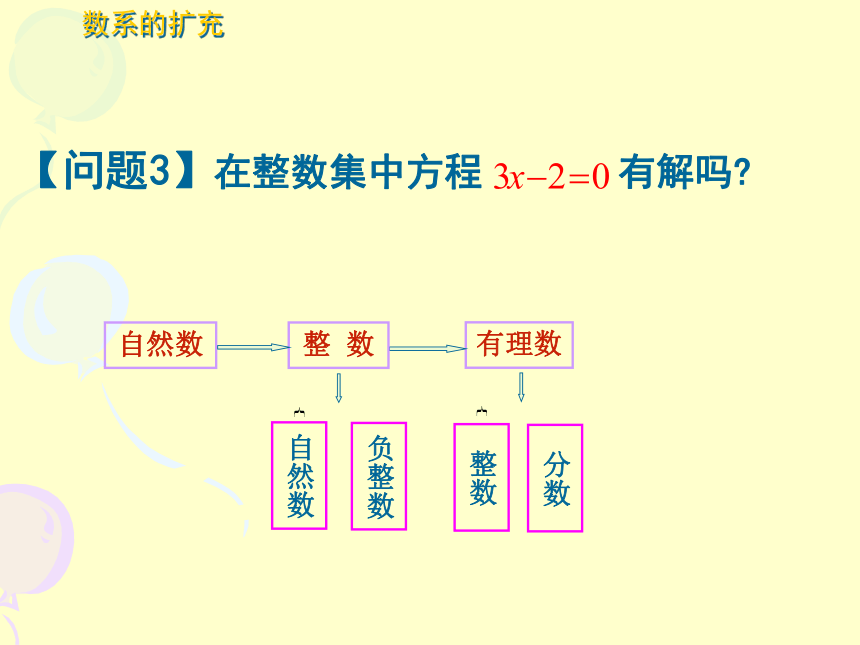
【问题3】在整数集中方程
有解吗?
自然数
整
数
自然数
负整数
实
数
有理数
无理数
SHUXI
DI
KUOCHONG
数系的扩充
【问题4】在有理数集中方程
有解吗?
有理数
整数
分数
自然数
整
数
自然数
负整数
在实数集中方程
有解吗?
【问题5】
SHUXI
DI
KUOCHONG
数系的扩充
【问题4】在有理数集中方程
有解吗?
在实数集中方程
有解吗?
【问题5】
没有实数根
学生活动
现在我们要进行数系的再
一次扩充就是要解决这个
问题,
怎么解决?
讨论
你能给出一个解决问题的方
案吗?
问题6:
引入一个新数:
满足
1637年,法国数学家笛卡尔把这样的数叫做“虚数”
SHUXI
DI
KUOCHONG
数系的扩充
(R.Descartes,1596--1661)
笛卡尔
1777年
欧拉首次提出用i表示平方等于-1的新数
Leonhard
Euler
(1707-1783)
欧
拉
1801年
高斯系统使用了i这个符号
使之通行于世
(1777—1855)
高
斯
Johann
Carl
Friedrich
Gauss
1.新数
i
叫做虚数单位,并规定:
(1)i
2
?
?1;
(2)实数可以与
i
进行四则运算,在进
行四则运算时,原有的加法与乘法
的运算律仍然成立.
SHUXI
DI
KUOCHONG
数系的扩充
(1)形如a+bi(a,b∈R)的数叫做复数,
通常用字母
z
表示.
(3)全体复数所形成的集合叫做复数
集,一般用字母
C
表示.
2.复数的概念
实部
虚部
其中
称为虚数单位.
(2)
SHUXI
DI
KUOCHONG
数系的扩充
复数集
虚数
SHUXI
DI
KUOCHONG
数系的扩充
?
实
数
集
有理数集
自然数集
整
数
集
整数
负整数
自然数
正整数
零
分数
有理数
无理数
实数
复数的分类:
复数z=a+bi
(a,b?R)
条件
数的类型
R
C
实数集R是复数集C的真子集,
虚数
b≠0
纯虚数
a=0且b≠0
实数0
a=b=0
实数
b=0
复数
z=a+bi
(a,b?R)
实数
(b=0)
虚数(b≠0)
纯虚数(a=0)
非纯虚数(a≠0)
N
Z
Q
R
C
复数集
虚数集
实数集
纯虚数集
1.写出下列复数的实部与虚部.
解:
4的实部为
4
,虚部为
0
;
2-3i的实部为
2
,虚部为
-3
;
0的实部为
0
,虚部为
0
;
的实部为
,虚部为
;
6i的实部为
0
,虚部为
6
。
2.说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。
5
+8,
0
3、判断下列命题是否正确:
(1)若a、b为实数,则Z=a+bi为虚数
(2)若b为实数,则Z=bi必为纯虚数
(3)若a为实数,则Z=
a一定不是虚数
例1
实数m取什么值时,
复数
是
(1)实数(2)虚数(3)纯虚数
解:(1)当
,即
时,复数z
是实数.
(2)当
,即
时,复数z
是虚数.
(3)当
时,复数z
是纯虚数.
(4)0
(5)6+2i
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
注意
1、若Z1,Z2均为实数,则Z1,Z2具有大小关系
2、若Z1,Z2中不都为实数,Z1与Z2只有相等或不相等两关系,而不能比较大小
例2:已知
复数相等的问题
转化
求方程组的解的问题
SHUXI
DI
KUOCHONG
数系的扩充
与
转化(复数问题实数化)
解:
根据两个复数相等的充要条件,
可得方程组
解得:
求实数
1、若x,y为实数,且
求x,y.
x=-3,y=4
2.若(2x2-3x-2)+(x2-5x+6)
=0,求x的值.
x=2
探究:任意两个复数可以比较大小吗?认为可以者,请拿出进行比较的方法;认为不可以者,请说明理由。
两个实数可以比较大小
实数与虚数不可以比较大小
虚数与虚数不可以比较大小
1
-1
B
1.将实数系扩充到复数系是源于解方程的需要,到十九世纪中叶已建立了一套完整的复数理论,形成一个独立的数学分支.
课堂小结
2.虚数单位i的引入解决了负数不能开平方的矛盾,并将实数集扩充到了复数集,它使得任何一个复数都可以写成
a+bi(a,b∈R)的形式.
3.复数包括了实数和虚数,实数的某些性质在复数集中不成立,如x2≥0;
若x-y>0,则x>y等,今后在数学解题中,如果没有特殊说明,一般都在实数集内解决问题.
4.复数有关概念:
复数的代数形式:
复数的实部
、虚部
复数相等
虚数、纯虚数
1、以2i-3的虚部为实部,3i+2i2的实部为虚部的复数是(
)
A.
2-2i
B.2+2i
C.
-3+3i
D.
3+3i
2、设全集I={复数},R={实数},M={纯虚数},那么(
)
A.
R∪M=I
B.
R∩M={?}
练习
A
B
练习
3、已知复数Z=(2m2-3m
-2)+(m2
-2m)i(m∈R)是:
(1)实数;(2)虚数;(3)纯虚数;
求m的值.
毕达哥拉斯(约公元前560—480年)
“数”是万物的本源,支配整个自然界和人类社会.世间一切事物都可归结为数或数的比例,这是世界所以美好和谐的源泉.
计数的需要
正整数
零
自然数
SHUXI
DI
KUOCHONG
数系的扩充
SHUXI
DI
KUOCHONG
数系的扩充
中国是世界上最早认识应用负数的
国家.早在2000多年前的《九章算术》
中,就有正数和负数的记载.在古代人民
生活中,以收入钱为正,以支出钱为负.在
粮食生产中,以产量增加为正,以产量减
少为负.古代的人们为区别正、负数,常
用红色算筹表示正,黑色算筹表示负.
小贴士
珠穆朗玛峰大约比海平面高8844米.
吐鲁番盆地大约比海平面低155米.
+8844
-155
SHUXI
DI
KUOCHONG
数系的扩充
自然数集
整数
负整数
自然数
正整数
零
整
数
集
SHUXI
DI
KUOCHONG
数系的扩充
整数
负整数
自然数
正整数
零
分数
有理数
有理数集
自然数集
整
数
集
1
1
问题:边长为1的正方形的对角线长度为多少?
SHUXI
DI
KUOCHONG
数系的扩充
有理数集
自然数集
整
数
集
整数
负整数
自然数
正整数
零
分数
有理数
无理数
实数
实
数
集
SHUXI
DI
KUOCHONG
数系的扩充
有理数集
自然数集
整
数
集
【问题1】在自然数集中方程
有解吗?
【问题2】在整数集中方程
有解吗?
自然数
整
数
自然数
负整数
SHUXI
DI
KUOCHONG
数系的扩充
有理数
整数
分数
SHUXI
DI
KUOCHONG
数系的扩充
【问题3】在整数集中方程
有解吗?
自然数
整
数
自然数
负整数
实
数
有理数
无理数
SHUXI
DI
KUOCHONG
数系的扩充
【问题4】在有理数集中方程
有解吗?
有理数
整数
分数
自然数
整
数
自然数
负整数
在实数集中方程
有解吗?
【问题5】
SHUXI
DI
KUOCHONG
数系的扩充
【问题4】在有理数集中方程
有解吗?
在实数集中方程
有解吗?
【问题5】
没有实数根
学生活动
现在我们要进行数系的再
一次扩充就是要解决这个
问题,
怎么解决?
讨论
你能给出一个解决问题的方
案吗?
问题6:
引入一个新数:
满足
1637年,法国数学家笛卡尔把这样的数叫做“虚数”
SHUXI
DI
KUOCHONG
数系的扩充
(R.Descartes,1596--1661)
笛卡尔
1777年
欧拉首次提出用i表示平方等于-1的新数
Leonhard
Euler
(1707-1783)
欧
拉
1801年
高斯系统使用了i这个符号
使之通行于世
(1777—1855)
高
斯
Johann
Carl
Friedrich
Gauss
1.新数
i
叫做虚数单位,并规定:
(1)i
2
?
?1;
(2)实数可以与
i
进行四则运算,在进
行四则运算时,原有的加法与乘法
的运算律仍然成立.
SHUXI
DI
KUOCHONG
数系的扩充
(1)形如a+bi(a,b∈R)的数叫做复数,
通常用字母
z
表示.
(3)全体复数所形成的集合叫做复数
集,一般用字母
C
表示.
2.复数的概念
实部
虚部
其中
称为虚数单位.
(2)
SHUXI
DI
KUOCHONG
数系的扩充
复数集
虚数
SHUXI
DI
KUOCHONG
数系的扩充
?
实
数
集
有理数集
自然数集
整
数
集
整数
负整数
自然数
正整数
零
分数
有理数
无理数
实数
复数的分类:
复数z=a+bi
(a,b?R)
条件
数的类型
R
C
实数集R是复数集C的真子集,
虚数
b≠0
纯虚数
a=0且b≠0
实数0
a=b=0
实数
b=0
复数
z=a+bi
(a,b?R)
实数
(b=0)
虚数(b≠0)
纯虚数(a=0)
非纯虚数(a≠0)
N
Z
Q
R
C
复数集
虚数集
实数集
纯虚数集
1.写出下列复数的实部与虚部.
解:
4的实部为
4
,虚部为
0
;
2-3i的实部为
2
,虚部为
-3
;
0的实部为
0
,虚部为
0
;
的实部为
,虚部为
;
6i的实部为
0
,虚部为
6
。
2.说明下列数中,那些是实数,哪些是虚数,哪些是纯虚数,并指出复数的实部与虚部。
5
+8,
0
3、判断下列命题是否正确:
(1)若a、b为实数,则Z=a+bi为虚数
(2)若b为实数,则Z=bi必为纯虚数
(3)若a为实数,则Z=
a一定不是虚数
例1
实数m取什么值时,
复数
是
(1)实数(2)虚数(3)纯虚数
解:(1)当
,即
时,复数z
是实数.
(2)当
,即
时,复数z
是虚数.
(3)当
时,复数z
是纯虚数.
(4)0
(5)6+2i
如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
注意
1、若Z1,Z2均为实数,则Z1,Z2具有大小关系
2、若Z1,Z2中不都为实数,Z1与Z2只有相等或不相等两关系,而不能比较大小
例2:已知
复数相等的问题
转化
求方程组的解的问题
SHUXI
DI
KUOCHONG
数系的扩充
与
转化(复数问题实数化)
解:
根据两个复数相等的充要条件,
可得方程组
解得:
求实数
1、若x,y为实数,且
求x,y.
x=-3,y=4
2.若(2x2-3x-2)+(x2-5x+6)
=0,求x的值.
x=2
探究:任意两个复数可以比较大小吗?认为可以者,请拿出进行比较的方法;认为不可以者,请说明理由。
两个实数可以比较大小
实数与虚数不可以比较大小
虚数与虚数不可以比较大小
1
-1
B
1.将实数系扩充到复数系是源于解方程的需要,到十九世纪中叶已建立了一套完整的复数理论,形成一个独立的数学分支.
课堂小结
2.虚数单位i的引入解决了负数不能开平方的矛盾,并将实数集扩充到了复数集,它使得任何一个复数都可以写成
a+bi(a,b∈R)的形式.
3.复数包括了实数和虚数,实数的某些性质在复数集中不成立,如x2≥0;
若x-y>0,则x>y等,今后在数学解题中,如果没有特殊说明,一般都在实数集内解决问题.
4.复数有关概念:
复数的代数形式:
复数的实部
、虚部
复数相等
虚数、纯虚数
1、以2i-3的虚部为实部,3i+2i2的实部为虚部的复数是(
)
A.
2-2i
B.2+2i
C.
-3+3i
D.
3+3i
2、设全集I={复数},R={实数},M={纯虚数},那么(
)
A.
R∪M=I
B.
R∩M={?}
练习
A
B
练习
3、已知复数Z=(2m2-3m
-2)+(m2
-2m)i(m∈R)是:
(1)实数;(2)虚数;(3)纯虚数;
求m的值.
