9.4乘法公式(2)—平方差公式 苏科版七年级数学下册课件 (共20张PPT)
文档属性
| 名称 | 9.4乘法公式(2)—平方差公式 苏科版七年级数学下册课件 (共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 965.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 10:29:35 | ||
图片预览






文档简介
1.借助图形推导完全平方公式,了解公式的几何背景.
2.经历探索平方差公式得过程,感受数形结合的思想,能利用公式进行简单计算.
学习目标
用完全平方公式计算:
(1) (2a-3)2
(2) (-x+4y)2
(3) (-a-2b)2 - (-a+2b)2
(4) 1022
(5) (-2a-b+c) 2
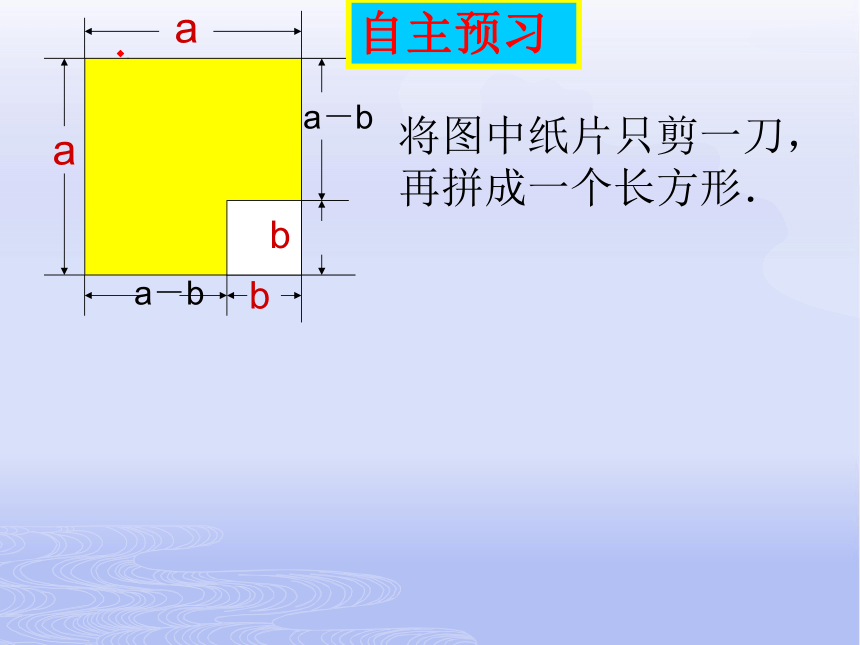
自主预习
将图中纸片只剪一刀,再拼成一个长方形.
a
a
b
b
a-b
a-b
自主预习
a
a
b
b
a-b
a-b
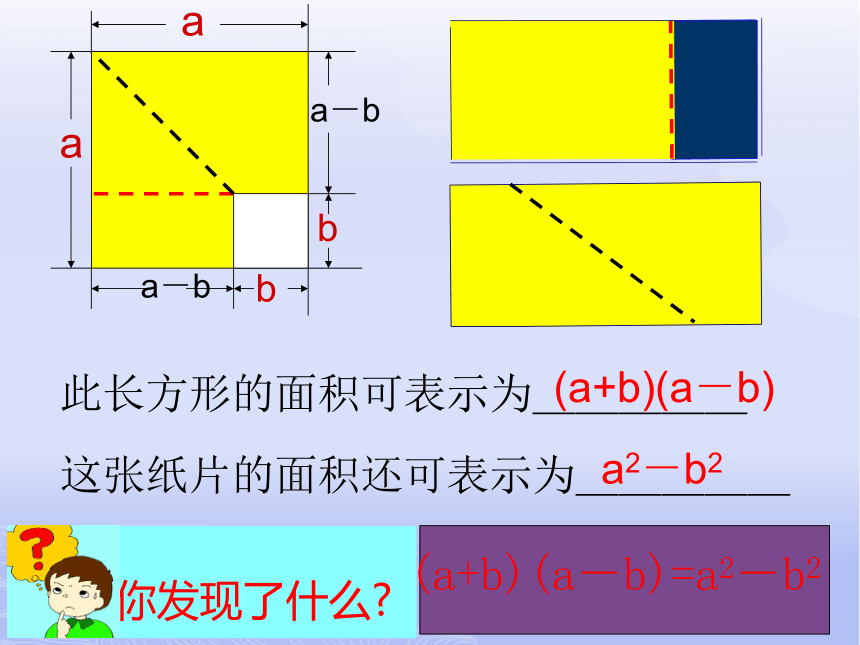
此长方形的面积可表示为_____
这张纸片的面积还可表示为_____
(a+b)(a-b)
a2-b2
你发现了什么?
(a+b)(a-b)=a2-b2
a
a
b
b
a-b
a-b
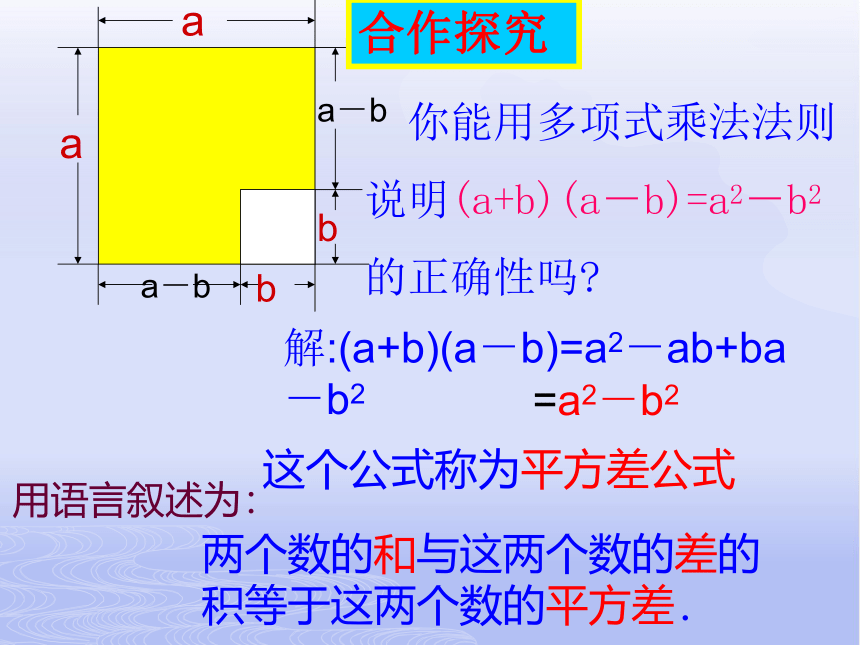
两个数的和与这两个数的差的积等于这两个数的平方差.
用语言叙述为:
这个公式称为平方差公式
你能用多项式乘法法则
说明(a+b)(a-b)=a2-b2
的正确性吗?
解:(a+b)(a-b)=a2-ab+ba-b2
=a2-b2
合作探究
平方差公式:
(a+b)(a-b)=a2-b2
1.用平方差公式计算:
(1) (x+2y)(x-2y)
(2) (2x+3)(2x-3)
(3) (-5-4y)(-5+4y)
合作探究
1.选择:下列各式中,能用平方差公式的是( )
A.(x-3)(-x+3) B.(x+2y)(2x-y)
C.(y-1)(-y-1) D.(y+1)(-y-1)
C
个性展示
×
√
×
×
3.填空:
3y
2x
4x2
- 4x+3y
2.判断:
(1)(x+3)(x-2)=x2-6 ( )
(2)(y+2)(x-2)=xy-4 ( )
(3)(2y+3)(-2y+3)=9-4y2 ( )
(4)(3-2y)2=9-4y2 ( )
(1)(2x-__)(__+3y)=____-9y2
(2)(______)(-4x-3y)=16x2-9y2
4.用平方差公式计算:
(1)(3x+2y)(3x-2y)
(2) (2x+3)(-3+2x)
(3) (-5-4y)(-5+4y)
(4) (-3x-2y)(3x+2y)
(3x-1)(3x+1) -(2x+3)(2x-3)
(6) (2x+y)( -y+2x)-(2x-y)2
1.用简便方法计算:
(1) 101×99
(2)
(1)22×18
(2)
整合提升
2.阅读下文件,寻找规律:已知x≠1,计算:
(1﹣x)(1+x)=1﹣x2
(1﹣x)(1+x+x2)=1﹣x3
(1﹣x)(1+x+x2+x3)=1﹣x4
(1﹣x)(1+x+x2+x3+x4)=1﹣x5 ……
(1)观察上式猜想:
(1﹣x)(1+x+x2+x3+…+xn)= . (2)根据你的猜想计算:
①1+2+22+23+24+…+22018 ②214+215+…+2100.
整合提升
(1)16x2-81; (2)x2-y2+2y-1;
(3)x2-2x+1-y2; (4)m4-8m2n2+16n4.
检测反馈
1.计算:
2.计算:
第(2)题先逆用积的乘方法则,再用平方差公式,最后用完全平方公式.
第(3)题将(x+y)看成整体,然后用平方差公式.
检测反馈
-4xy; -8
3.化简求值:
4.已知(a+b)2=7,(a-b)2=3.
求:(1)a2+b2 ; (2)ab的值.
解:∵(a+b)2=7,(a-b)2=3
∴a2+2ab+b2=7 ①
a2-2ab+b2=3 ②
∴①+②, 得:a2+b2=5
①-②, 得:ab=1.
5.观察下面各式规律:
2×4+1=9,
4×6+1=25,
6×8+1=49,……
写出第n个等式,并证明你的结论.
2n· (2n+2)+1=(2n+1)2
6.若a、b满足a2+b2-4a+6b+13=0,
求代数式(a+b)2020的值.
2.张老师在黑板上写了三个算式,希望同学们认真观察,发现规律.请你结合这些算式,解答下列问题:
请观察以下算式:
①32﹣12=8×1 ②52﹣32=8×2 ③72﹣52=8×3
(1)请你再写出另外两个符合上述规律的算式;
(2)验证规律:设两个连续奇数为2n+1,2n﹣1(其中n为正整数),则它们的平方差是8的倍数;
(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?
这节课,我的收获是---
小结与回顾
(1)掌握平方差公式的特点
平方差公式的结果是两项
(2) 能利用平方差公式进行计算
作业
课本87页 2,4. (5)-(8)
5.(2)
2.经历探索平方差公式得过程,感受数形结合的思想,能利用公式进行简单计算.
学习目标
用完全平方公式计算:
(1) (2a-3)2
(2) (-x+4y)2
(3) (-a-2b)2 - (-a+2b)2
(4) 1022
(5) (-2a-b+c) 2
自主预习
将图中纸片只剪一刀,再拼成一个长方形.
a
a
b
b
a-b
a-b
自主预习
a
a
b
b
a-b
a-b
此长方形的面积可表示为_____
这张纸片的面积还可表示为_____
(a+b)(a-b)
a2-b2
你发现了什么?
(a+b)(a-b)=a2-b2
a
a
b
b
a-b
a-b
两个数的和与这两个数的差的积等于这两个数的平方差.
用语言叙述为:
这个公式称为平方差公式
你能用多项式乘法法则
说明(a+b)(a-b)=a2-b2
的正确性吗?
解:(a+b)(a-b)=a2-ab+ba-b2
=a2-b2
合作探究
平方差公式:
(a+b)(a-b)=a2-b2
1.用平方差公式计算:
(1) (x+2y)(x-2y)
(2) (2x+3)(2x-3)
(3) (-5-4y)(-5+4y)
合作探究
1.选择:下列各式中,能用平方差公式的是( )
A.(x-3)(-x+3) B.(x+2y)(2x-y)
C.(y-1)(-y-1) D.(y+1)(-y-1)
C
个性展示
×
√
×
×
3.填空:
3y
2x
4x2
- 4x+3y
2.判断:
(1)(x+3)(x-2)=x2-6 ( )
(2)(y+2)(x-2)=xy-4 ( )
(3)(2y+3)(-2y+3)=9-4y2 ( )
(4)(3-2y)2=9-4y2 ( )
(1)(2x-__)(__+3y)=____-9y2
(2)(______)(-4x-3y)=16x2-9y2
4.用平方差公式计算:
(1)(3x+2y)(3x-2y)
(2) (2x+3)(-3+2x)
(3) (-5-4y)(-5+4y)
(4) (-3x-2y)(3x+2y)
(3x-1)(3x+1) -(2x+3)(2x-3)
(6) (2x+y)( -y+2x)-(2x-y)2
1.用简便方法计算:
(1) 101×99
(2)
(1)22×18
(2)
整合提升
2.阅读下文件,寻找规律:已知x≠1,计算:
(1﹣x)(1+x)=1﹣x2
(1﹣x)(1+x+x2)=1﹣x3
(1﹣x)(1+x+x2+x3)=1﹣x4
(1﹣x)(1+x+x2+x3+x4)=1﹣x5 ……
(1)观察上式猜想:
(1﹣x)(1+x+x2+x3+…+xn)= . (2)根据你的猜想计算:
①1+2+22+23+24+…+22018 ②214+215+…+2100.
整合提升
(1)16x2-81; (2)x2-y2+2y-1;
(3)x2-2x+1-y2; (4)m4-8m2n2+16n4.
检测反馈
1.计算:
2.计算:
第(2)题先逆用积的乘方法则,再用平方差公式,最后用完全平方公式.
第(3)题将(x+y)看成整体,然后用平方差公式.
检测反馈
-4xy; -8
3.化简求值:
4.已知(a+b)2=7,(a-b)2=3.
求:(1)a2+b2 ; (2)ab的值.
解:∵(a+b)2=7,(a-b)2=3
∴a2+2ab+b2=7 ①
a2-2ab+b2=3 ②
∴①+②, 得:a2+b2=5
①-②, 得:ab=1.
5.观察下面各式规律:
2×4+1=9,
4×6+1=25,
6×8+1=49,……
写出第n个等式,并证明你的结论.
2n· (2n+2)+1=(2n+1)2
6.若a、b满足a2+b2-4a+6b+13=0,
求代数式(a+b)2020的值.
2.张老师在黑板上写了三个算式,希望同学们认真观察,发现规律.请你结合这些算式,解答下列问题:
请观察以下算式:
①32﹣12=8×1 ②52﹣32=8×2 ③72﹣52=8×3
(1)请你再写出另外两个符合上述规律的算式;
(2)验证规律:设两个连续奇数为2n+1,2n﹣1(其中n为正整数),则它们的平方差是8的倍数;
(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?
这节课,我的收获是---
小结与回顾
(1)掌握平方差公式的特点
平方差公式的结果是两项
(2) 能利用平方差公式进行计算
作业
课本87页 2,4. (5)-(8)
5.(2)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
