苏科版八年级数学下册:9.3 平行四边形(3)课件(共15张PPT)
文档属性
| 名称 | 苏科版八年级数学下册:9.3 平行四边形(3)课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 11:00:13 | ||
图片预览






文档简介
9.3 平行四边形(3)
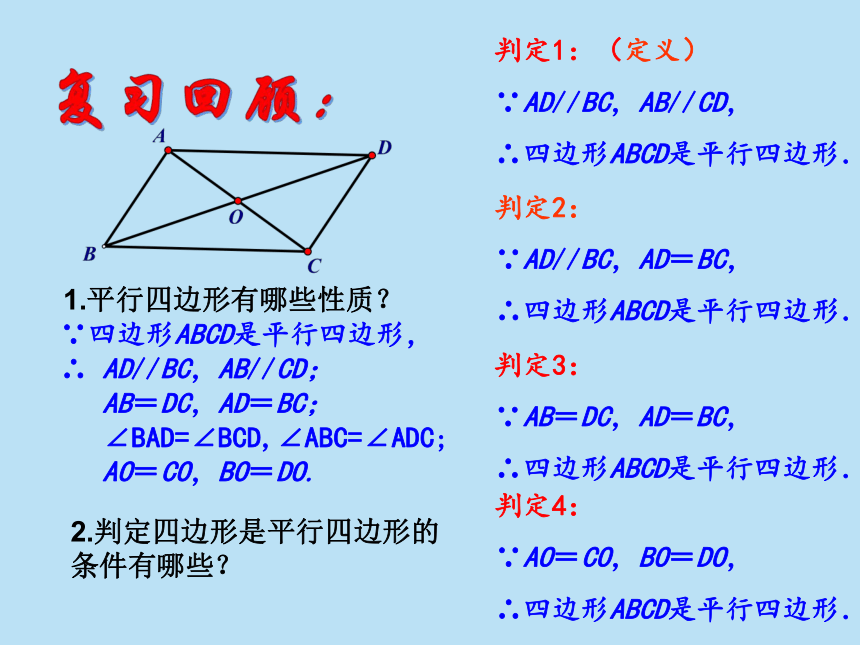
判定1:(定义)
∵AD//BC,AB//CD,
∴四边形ABCD是平行四边形.
判定2:
∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形.
判定3:
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
判定4:
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形.
1.平行四边形有哪些性质?
∵四边形ABCD是平行四边形,
∴ AD//BC,AB//CD;
AB=DC,AD=BC;
∠BAD=∠BCD,∠ABC=∠ADC;
AO=CO,BO=DO.
2.判定四边形是平行四边形的条件有哪些?
画□ABCD,使AB=2㎝,BC=3㎝,AC=4㎝。想一想,画出ΔABC后,你能用哪些方法确定点D的位置?说明理由。
分析:如何画ΔABC?如何确定点D的位置?理由是?
根据SSS,画出ΔABC。
1、画线段AC=4㎝;
2、分别以A、C为圆心,2㎝,3㎝为半径画弧;两弧相交于点B;
3、连接AB、BC,即得到ΔABC。
画□ABCD,使AB=2㎝,BC=3㎝,AC=4㎝。想一想,画出ΔABC后,你能用哪些方法确定点D的位置?说明理由。
判定1:∵AD//BC,AB//CD,
∴四边形ABCD是平行四边形.
判定2: ∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形.
判定3: ∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
判定4: ∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
变式:画出ΔABC,使AB=2㎝,BC=3㎝,AC=4㎝。确定一点D,使得以A、B、C、D为顶点的四边形是平行四边形。
以AC为对角线
□ABCD
分析:可以以ΔABC的三条边中哪一条是平行四边形的对角线进行分类,先确定平行四边形四个顶点的顺序。
以BC为对角线
□ABDC
以AB为对角线
□ACBD
如果OA=OC,OB≠OD,那么四边形ABCD不是平行四边形.试证明这个结论。
证明:
假设四边形ABCD是平行四边形,
那么OA=OC,BO=OD,
这与条件“OB≠OD”矛盾.
所以四边形ABCD不是平行四边形.
阅读:
书本P71阅读:趣谈“反证法”
数学中
运用反证法
证明命题的步骤:
1、假设结论的反面成立;
2、从假设出发,推出矛盾的结果;
3、说明假设错误,得出结论成立。
想一想:
反证法和举反例的区别
1、假设结论的反面成立;
2、从假设出发,推出矛盾的结果;
3、说明假设错误,得出结论成立。
如果OA=OC,OB≠OD,
那么四边形ABCD不是平行四边形.(书P69讨论)
一组对边平行,另一组对边相等的四边形是平行四边形吗?如果是,加以证明,如果不是,举出反例。
(书P68练习3)
反例:
满足命题的条件,
但不满足命题的结论。
“一组对边平行,另一组对边相等的四边形是平行四边形。”是假命题。
举反例的方法用于说明命题是假命题。
例1、如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别是E、F,求证:四边形AECF是平行四边形.
证明:∵在□ABCD中,有:
AB∥CD,AB=CD;
∴∠ABD=CDB.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠AED=90°,
∠CFD=CFB=90°.
∵在ΔABE和ΔCDF中,
∠ABD=CDB
∠AEB=∠CFD=90°
AB=CD
∴ ΔABE≌ΔCDF(AAS)
∴ AE=CF.
∵ ∠AED=CFB=90°
∴ AE∥CF.
∵AE∥CF, AE=CF,
∴四边形AECF是平行四边形.
另解:也可以从对角线入手,连接AC
性质+判定2
例2、如图, □ABCD中,E、F为边AD、BC上的点,AE=CF,连接AF、EC、BE、DF交于点M、N
求证:线段MN、EF互相平分
平行四边形MFNE
AF∥CE ,BE∥DF,
平行四边形AFCE
平行四边形BEDF
AE=CF,AE∥CF
DE∥BF ,DE=BF,
AD=BC,AE=CF
平行四边形ABCD
分析:
例2、如图, 在□ABCD中,E、F为边AD、BC上的点,AE=CF,连接AF、EC、BE、DF交于点M、N
求证:线段MN、EF互相平分
证明:
平行四边形ABCD中,有
AD∥BC,AD=BC;
又∵AE=CF
∴AD-AE=BC-CF
∴ED=BF
∵AE∥CF,AE=CF;
∴四边形AECF是平行四边形;
∴ AF∥CE
∵DE∥BF,DE=BF;
∴四边形DEBF是平行四边形;
∴BE∥DF
∵AF∥CE,BE∥DF;
∴四边形EMFN是平行四边形。
∴MN、EF互相平分。
性质+判定2+判定1
例3、已知:如图,在□ABCD中,对角线AC,BD相交于点O. G、H分别是OB、OD的中点,过点O的直线分别交BC、AD于F、E.
求证:四边形GEHF是平行四边形.
证明:在□ABCD中,有:
AO=CO,BO=DO, AD//BC.
∵在ΔAOE和ΔC0F中,
∠1=∠2
A0=CO
∠3=∠4
∴ ΔAOE≌ΔCOF(ASA)
∴ OE=OF.
性质+判定4
∵EO=OF,GO=OH;
∴四边形GEHF是平行四边形。
2、熟悉用反证法证明了一个命题的步骤和原理;
思考:如果一个四边形中有一组对角不相等,那么这个四边形是平行四边形吗?证明你的结论。
1、综合运用平行四边形的性质定理和判定定理解决了一些问题;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}平行四边形
性质
判定
边的关系
对边平行
对边相等
两组对边分别平行的四边形
两组对边分别相等的四边形
一组对边平行且相等的四边形
角的关系
对角相等
对角线的关系
对角线互相平分
对角线互相平分的四边形
课堂小结:
练习1、已知:如图,点E、F、G、H分别在□ABCD的各边上,AE=CG,BF=DH.求证:EH∥GF.
证明:连接EF、GH.
在□ABCD中,有:
AB=CD,BC=AD,∠A=∠C,∠B=∠D
又∵ AE=CG,BF=DH
∴AB-AE=CD-CG,BC-BF=AD-DH
∴BE=DG,CF=AH
∵在ΔAHE和ΔCFG中,
AH=CF
∠A=∠C
AE=CG
∴ ΔAHE≌ΔCFG(ASA)
∴ EH=GF.
∵在ΔBEF和ΔDGH中,
BE=DG
∠B=∠D
BF=DH
∴ ΔBEF≌ΔDGH(ASA)
∴ EF=GH.
∵EH=GF,EF=GH;
∴四边形EFGH是平行四边形。
∴ EH∥GF.
性质+判定3
练习2、已知:在□ABCD中, ∠BAD与∠BCD的角平分线AE、CF分别交DC、BA的延长线于E、F。
证明:AF=CE.
分析:
□AFCE
AF∥CE CF∥AE
∠1=∠F
∠F=∠2 ∠1=∠2
AE、CF 为∠BAD与∠BCD的角平分线
AB∥CD
谢谢聆听!
判定1:(定义)
∵AD//BC,AB//CD,
∴四边形ABCD是平行四边形.
判定2:
∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形.
判定3:
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
判定4:
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形.
1.平行四边形有哪些性质?
∵四边形ABCD是平行四边形,
∴ AD//BC,AB//CD;
AB=DC,AD=BC;
∠BAD=∠BCD,∠ABC=∠ADC;
AO=CO,BO=DO.
2.判定四边形是平行四边形的条件有哪些?
画□ABCD,使AB=2㎝,BC=3㎝,AC=4㎝。想一想,画出ΔABC后,你能用哪些方法确定点D的位置?说明理由。
分析:如何画ΔABC?如何确定点D的位置?理由是?
根据SSS,画出ΔABC。
1、画线段AC=4㎝;
2、分别以A、C为圆心,2㎝,3㎝为半径画弧;两弧相交于点B;
3、连接AB、BC,即得到ΔABC。
画□ABCD,使AB=2㎝,BC=3㎝,AC=4㎝。想一想,画出ΔABC后,你能用哪些方法确定点D的位置?说明理由。
判定1:∵AD//BC,AB//CD,
∴四边形ABCD是平行四边形.
判定2: ∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形.
判定3: ∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形.
判定4: ∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
变式:画出ΔABC,使AB=2㎝,BC=3㎝,AC=4㎝。确定一点D,使得以A、B、C、D为顶点的四边形是平行四边形。
以AC为对角线
□ABCD
分析:可以以ΔABC的三条边中哪一条是平行四边形的对角线进行分类,先确定平行四边形四个顶点的顺序。
以BC为对角线
□ABDC
以AB为对角线
□ACBD
如果OA=OC,OB≠OD,那么四边形ABCD不是平行四边形.试证明这个结论。
证明:
假设四边形ABCD是平行四边形,
那么OA=OC,BO=OD,
这与条件“OB≠OD”矛盾.
所以四边形ABCD不是平行四边形.
阅读:
书本P71阅读:趣谈“反证法”
数学中
运用反证法
证明命题的步骤:
1、假设结论的反面成立;
2、从假设出发,推出矛盾的结果;
3、说明假设错误,得出结论成立。
想一想:
反证法和举反例的区别
1、假设结论的反面成立;
2、从假设出发,推出矛盾的结果;
3、说明假设错误,得出结论成立。
如果OA=OC,OB≠OD,
那么四边形ABCD不是平行四边形.(书P69讨论)
一组对边平行,另一组对边相等的四边形是平行四边形吗?如果是,加以证明,如果不是,举出反例。
(书P68练习3)
反例:
满足命题的条件,
但不满足命题的结论。
“一组对边平行,另一组对边相等的四边形是平行四边形。”是假命题。
举反例的方法用于说明命题是假命题。
例1、如图,在□ABCD中,AE⊥BD,CF⊥BD,垂足分别是E、F,求证:四边形AECF是平行四边形.
证明:∵在□ABCD中,有:
AB∥CD,AB=CD;
∴∠ABD=CDB.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠AED=90°,
∠CFD=CFB=90°.
∵在ΔABE和ΔCDF中,
∠ABD=CDB
∠AEB=∠CFD=90°
AB=CD
∴ ΔABE≌ΔCDF(AAS)
∴ AE=CF.
∵ ∠AED=CFB=90°
∴ AE∥CF.
∵AE∥CF, AE=CF,
∴四边形AECF是平行四边形.
另解:也可以从对角线入手,连接AC
性质+判定2
例2、如图, □ABCD中,E、F为边AD、BC上的点,AE=CF,连接AF、EC、BE、DF交于点M、N
求证:线段MN、EF互相平分
平行四边形MFNE
AF∥CE ,BE∥DF,
平行四边形AFCE
平行四边形BEDF
AE=CF,AE∥CF
DE∥BF ,DE=BF,
AD=BC,AE=CF
平行四边形ABCD
分析:
例2、如图, 在□ABCD中,E、F为边AD、BC上的点,AE=CF,连接AF、EC、BE、DF交于点M、N
求证:线段MN、EF互相平分
证明:
平行四边形ABCD中,有
AD∥BC,AD=BC;
又∵AE=CF
∴AD-AE=BC-CF
∴ED=BF
∵AE∥CF,AE=CF;
∴四边形AECF是平行四边形;
∴ AF∥CE
∵DE∥BF,DE=BF;
∴四边形DEBF是平行四边形;
∴BE∥DF
∵AF∥CE,BE∥DF;
∴四边形EMFN是平行四边形。
∴MN、EF互相平分。
性质+判定2+判定1
例3、已知:如图,在□ABCD中,对角线AC,BD相交于点O. G、H分别是OB、OD的中点,过点O的直线分别交BC、AD于F、E.
求证:四边形GEHF是平行四边形.
证明:在□ABCD中,有:
AO=CO,BO=DO, AD//BC.
∵在ΔAOE和ΔC0F中,
∠1=∠2
A0=CO
∠3=∠4
∴ ΔAOE≌ΔCOF(ASA)
∴ OE=OF.
性质+判定4
∵EO=OF,GO=OH;
∴四边形GEHF是平行四边形。
2、熟悉用反证法证明了一个命题的步骤和原理;
思考:如果一个四边形中有一组对角不相等,那么这个四边形是平行四边形吗?证明你的结论。
1、综合运用平行四边形的性质定理和判定定理解决了一些问题;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}平行四边形
性质
判定
边的关系
对边平行
对边相等
两组对边分别平行的四边形
两组对边分别相等的四边形
一组对边平行且相等的四边形
角的关系
对角相等
对角线的关系
对角线互相平分
对角线互相平分的四边形
课堂小结:
练习1、已知:如图,点E、F、G、H分别在□ABCD的各边上,AE=CG,BF=DH.求证:EH∥GF.
证明:连接EF、GH.
在□ABCD中,有:
AB=CD,BC=AD,∠A=∠C,∠B=∠D
又∵ AE=CG,BF=DH
∴AB-AE=CD-CG,BC-BF=AD-DH
∴BE=DG,CF=AH
∵在ΔAHE和ΔCFG中,
AH=CF
∠A=∠C
AE=CG
∴ ΔAHE≌ΔCFG(ASA)
∴ EH=GF.
∵在ΔBEF和ΔDGH中,
BE=DG
∠B=∠D
BF=DH
∴ ΔBEF≌ΔDGH(ASA)
∴ EF=GH.
∵EH=GF,EF=GH;
∴四边形EFGH是平行四边形。
∴ EH∥GF.
性质+判定3
练习2、已知:在□ABCD中, ∠BAD与∠BCD的角平分线AE、CF分别交DC、BA的延长线于E、F。
证明:AF=CE.
分析:
□AFCE
AF∥CE CF∥AE
∠1=∠F
∠F=∠2 ∠1=∠2
AE、CF 为∠BAD与∠BCD的角平分线
AB∥CD
谢谢聆听!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
