苏科版八年级下册 9.4 正方形课件(共21张PPT)
文档属性
| 名称 | 苏科版八年级下册 9.4 正方形课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 488.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 11:00:43 | ||
图片预览






文档简介
9.4 正 方 形
1.探究正方形的判定和性质.
2.会用正方形的性质和判定解决问题.
学习目标
1.从长方形木板中怎样截出最大的正方形木板?
2.怎样使菱形的衣帽架变成正方形的衣帽架?
\
\
∟
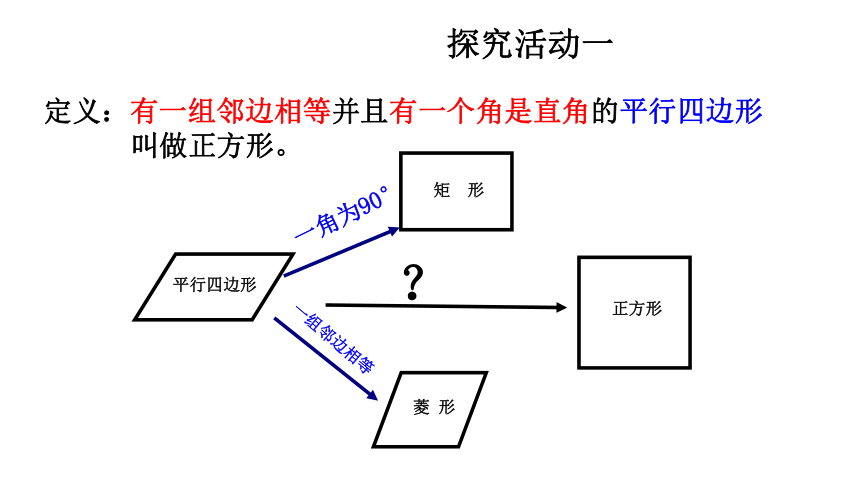
探究活动一
平行四边形
矩 形
菱 形
一角为90°
一组邻边相等
?
正方形
定义:有一组邻边相等并且有一个角是直角的平行四边形
叫做正方形。
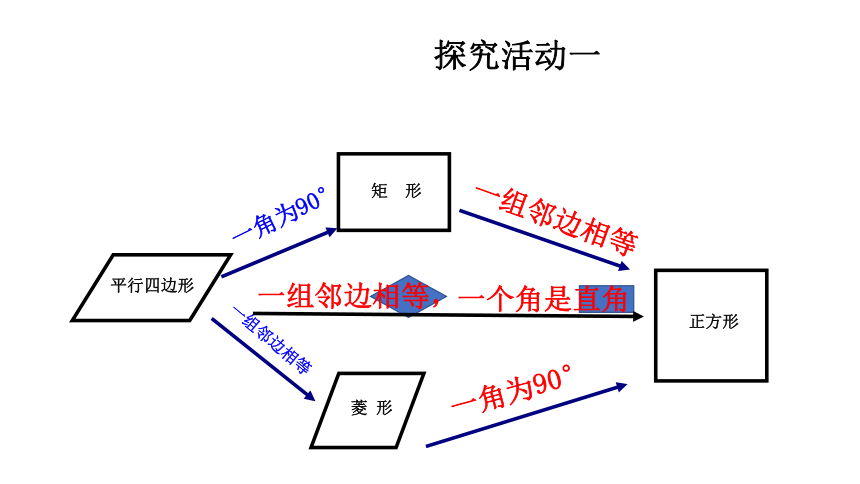
探究活动一
平行四边形
矩 形
菱 形
一角为90°
一组邻边相等
一组邻边相等,
正方形
一组邻边相等
一角为90°
一个角是直角
探究活动一
于是我们得出如下定理:
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
探究活动一
1.有一组邻边相等并且有一个角是直角的
平行四边形是正方形.(定义)
3.有一个角是直角的菱形是正方形.
2.有一组邻边相等的矩形是正方形.
正方形的判定方法:
探究活动一
例1 已知:如图,△ABC中.∠ABC=90°,BD是∠ABC平分线,DE⊥AB,DF⊥BC,垂足分别是E、F.证明四边形DEBF是正方形.
F
A
B
C
D
E
解:∵ DF⊥BC,DE⊥AB,
∴ ∠DEB= ∠DFB=90°,
又∵ ∠ABC=90°,
∴四边形DEBF是矩形
∵ BD平分∠ABC, DF⊥BC , DE⊥AB,
∴ DE= DF
∴四边形DEBF是正方形
×
×
∟
∟
∟
〃
〃
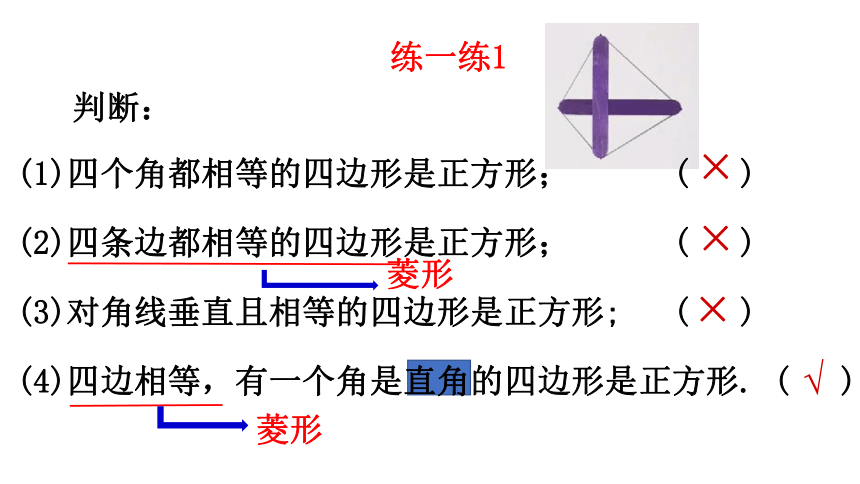
判断:
(1)四个角都相等的四边形是正方形; ( )
(2)四条边都相等的四边形是正方形; ( )
(3)对角线垂直且相等的四边形是正方形; ( )
(4)四边相等,有一个角是直角的四边形是正方形. ( )
√
×
×
×
练一练1
菱形
菱形
判断:
(5)对角线相等的菱形是正方形; ( )
(6)对角线互相垂直的矩形是正方形; ( )
√
√
A
A
B
B
C
C
D
D
O
O
矩形特有性质:
四个角是直角;
对角线相等.
菱形特有性质:
四边相等;
对角线互相垂直.
练一练1
平行四边形、
矩形、菱形、正
方形的关系如图:
平行四边形
矩形
菱形
正
方
形
正方形具有矩形的性质,
同时又具有菱形的性质.
对称性:
正方形既是轴对称图形,
又是中心对称图形
探究活动二
性 质
边
角
对角线
图形语言
文字语言
A
C
D
B
A
C
D
B
A
C
D
B
\
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等
性 质
边
角
对角线
图形语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,
OA=OC= AC
OB=OD= BD
45°
1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角
2.已知正方形的一条边长为2cm,则这个正方形的
周长为 ,对角线长为 ,面积为 .
8cm
C
轻松过关:
C
D
B
O
\
\
\
\
A
∟
45°
3.已知正方形ABCD中,对角线AC=10cm,P为AB上任意一点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF= .
A
B
C
D
F
P
E
O
5cm
轻松过关:
∟
∟
∟
\
\
\
\
例1 已知:如图,在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,求证∠MFD=45°.
要证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
△CMD≌△ADF
要证MD=FD,就是要证
分析:
试一试
看能不能完成证明???
证明:
∵正方形ABCD,且CE⊥AF
∴∠ADC=∠AEM=90°,CD=AD
又∵∠CMD=∠AME
∴∠1=∠2
又∵CD=AD,∠ADF=∠MDC
∴Rt△CDM≌Rt△ADF (ASA)
∴DM=DF,又∵∠MDF=90°
∴∠MFD=∠FMD=45°.
1. 已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,证明四边形EFGH是正方形.
A
B
C
D
E
F
G
H
1
2
3
证明:∵ 四边形ABCD是正方形
∴ ∠A=∠B=∠C=∠D=90°;
AB=AD=DC=BC
(正方形的四条边都相等,四个角都是直角)
又∵ AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴ △AEH≌△BFE≌△CGF ≌△DHG.
∴ EH=HG=GF=FE, ∠1=∠3
∴ 四边形EFGH是菱形
\
\
\
\
又∵ ∠3+∠2=90°且 ∠1=∠3
∴ ∠1+∠2=90°
∴ ∠EFG=90°
∴ 四边形EFGH是正方形
练一练2
2 如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。求证:∠CEA=∠ABG
证明:∵四边形ABDE和四边形ACFG是正方形.
∴AE=AB AG=AC ∠1=∠2=90°
又∵∠EAC=∠1+∠BAC=90°+∠BAC
∠BAG=∠2+∠BAC=90°+∠BAC
∴∠EAC=∠BAG
∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
M
正方形的定义
【归纳总结】
正方形的性质
运用正方形的判定
和性质解决问题
知识点
基本图形:
等腰直角三角形
\
\
\
\
∟
1.探究正方形的判定和性质.
2.会用正方形的性质和判定解决问题.
学习目标
1.从长方形木板中怎样截出最大的正方形木板?
2.怎样使菱形的衣帽架变成正方形的衣帽架?
\
\
∟
探究活动一
平行四边形
矩 形
菱 形
一角为90°
一组邻边相等
?
正方形
定义:有一组邻边相等并且有一个角是直角的平行四边形
叫做正方形。
探究活动一
平行四边形
矩 形
菱 形
一角为90°
一组邻边相等
一组邻边相等,
正方形
一组邻边相等
一角为90°
一个角是直角
探究活动一
于是我们得出如下定理:
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
探究活动一
1.有一组邻边相等并且有一个角是直角的
平行四边形是正方形.(定义)
3.有一个角是直角的菱形是正方形.
2.有一组邻边相等的矩形是正方形.
正方形的判定方法:
探究活动一
例1 已知:如图,△ABC中.∠ABC=90°,BD是∠ABC平分线,DE⊥AB,DF⊥BC,垂足分别是E、F.证明四边形DEBF是正方形.
F
A
B
C
D
E
解:∵ DF⊥BC,DE⊥AB,
∴ ∠DEB= ∠DFB=90°,
又∵ ∠ABC=90°,
∴四边形DEBF是矩形
∵ BD平分∠ABC, DF⊥BC , DE⊥AB,
∴ DE= DF
∴四边形DEBF是正方形
×
×
∟
∟
∟
〃
〃
判断:
(1)四个角都相等的四边形是正方形; ( )
(2)四条边都相等的四边形是正方形; ( )
(3)对角线垂直且相等的四边形是正方形; ( )
(4)四边相等,有一个角是直角的四边形是正方形. ( )
√
×
×
×
练一练1
菱形
菱形
判断:
(5)对角线相等的菱形是正方形; ( )
(6)对角线互相垂直的矩形是正方形; ( )
√
√
A
A
B
B
C
C
D
D
O
O
矩形特有性质:
四个角是直角;
对角线相等.
菱形特有性质:
四边相等;
对角线互相垂直.
练一练1
平行四边形、
矩形、菱形、正
方形的关系如图:
平行四边形
矩形
菱形
正
方
形
正方形具有矩形的性质,
同时又具有菱形的性质.
对称性:
正方形既是轴对称图形,
又是中心对称图形
探究活动二
性 质
边
角
对角线
图形语言
文字语言
A
C
D
B
A
C
D
B
A
C
D
B
\
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等
性 质
边
角
对角线
图形语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,
OA=OC= AC
OB=OD= BD
45°
1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角
2.已知正方形的一条边长为2cm,则这个正方形的
周长为 ,对角线长为 ,面积为 .
8cm
C
轻松过关:
C
D
B
O
\
\
\
\
A
∟
45°
3.已知正方形ABCD中,对角线AC=10cm,P为AB上任意一点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF= .
A
B
C
D
F
P
E
O
5cm
轻松过关:
∟
∟
∟
\
\
\
\
例1 已知:如图,在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M,求证∠MFD=45°.
要证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
△CMD≌△ADF
要证MD=FD,就是要证
分析:
试一试
看能不能完成证明???
证明:
∵正方形ABCD,且CE⊥AF
∴∠ADC=∠AEM=90°,CD=AD
又∵∠CMD=∠AME
∴∠1=∠2
又∵CD=AD,∠ADF=∠MDC
∴Rt△CDM≌Rt△ADF (ASA)
∴DM=DF,又∵∠MDF=90°
∴∠MFD=∠FMD=45°.
1. 已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,证明四边形EFGH是正方形.
A
B
C
D
E
F
G
H
1
2
3
证明:∵ 四边形ABCD是正方形
∴ ∠A=∠B=∠C=∠D=90°;
AB=AD=DC=BC
(正方形的四条边都相等,四个角都是直角)
又∵ AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴ △AEH≌△BFE≌△CGF ≌△DHG.
∴ EH=HG=GF=FE, ∠1=∠3
∴ 四边形EFGH是菱形
\
\
\
\
又∵ ∠3+∠2=90°且 ∠1=∠3
∴ ∠1+∠2=90°
∴ ∠EFG=90°
∴ 四边形EFGH是正方形
练一练2
2 如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。求证:∠CEA=∠ABG
证明:∵四边形ABDE和四边形ACFG是正方形.
∴AE=AB AG=AC ∠1=∠2=90°
又∵∠EAC=∠1+∠BAC=90°+∠BAC
∠BAG=∠2+∠BAC=90°+∠BAC
∴∠EAC=∠BAG
∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
M
正方形的定义
【归纳总结】
正方形的性质
运用正方形的判定
和性质解决问题
知识点
基本图形:
等腰直角三角形
\
\
\
\
∟
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
