苏科版八年级下册9.4矩形课件(共17张PPT)
文档属性
| 名称 | 苏科版八年级下册9.4矩形课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 308.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 13:07:19 | ||
图片预览






文档简介
矩形的性质
【教学目标】
1.理解矩形的概念,明确矩形与平行四边形的区别与联系
2.探索并证明矩形的性质,会用矩形的性质解决简单的问题
【重点】
矩形性质的探索、证明和应用
【难点】
灵活应用矩形的性质解决问题
课前思考
四名学生正在做投圈游戏,他们分别站在一个平行四边形的四个顶点处,目标物在对角线的交点处,小明认为这一队形对每个人不公平,如果改变平行四边形的一个角,让这个角是直角,那么这个游戏才公平,你知道这是为什么吗?
学习新知
矩形的定义:
有一个角是直角的平行四边形是矩形
探究未知
矩形的角、对角线有什么特殊性呢?
发现一
矩形的四个角都是直角
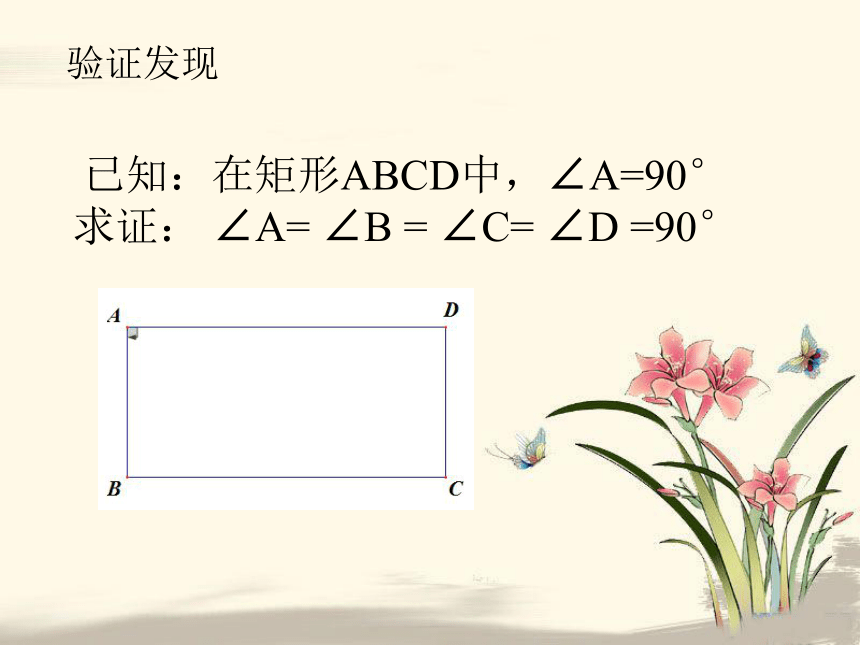
已知:在矩形ABCD中,∠A=90°
求证: ∠A= ∠B = ∠C= ∠D =90°
验证发现
得出结论
矩形的性质一:
矩形的四个角都是直角
发现二
矩形的对角线相等
推理验证
请同学们小组合作完成第二个发现的数学证明,比一比哪个小组做得最快
得出结论
矩形的性质二:
矩形的对角线相等
【应用新知】
例1 如图,在矩形ABCD中,对角线AC、BD相交于点O,下列说法错误的是( )
【A】∠ABC=90°
【B】AC=BD
【C】OA=OB
【D】OA=AB
【应用新知】
例2 如图,矩形ABCD 对角线AC、BD相交于点O, ∠AOB=60°,AB=4,求矩形对角线的长
一个矩形的一条对角线长为8,两条对角线的一个交角为120°,求这个矩形的边长(保留根号)
【课堂练习】
【课堂小结】
本节课你有哪些收获?
课堂小测
课后作业
教材第53页练习第3题
【教学目标】
1.理解矩形的概念,明确矩形与平行四边形的区别与联系
2.探索并证明矩形的性质,会用矩形的性质解决简单的问题
【重点】
矩形性质的探索、证明和应用
【难点】
灵活应用矩形的性质解决问题
课前思考
四名学生正在做投圈游戏,他们分别站在一个平行四边形的四个顶点处,目标物在对角线的交点处,小明认为这一队形对每个人不公平,如果改变平行四边形的一个角,让这个角是直角,那么这个游戏才公平,你知道这是为什么吗?
学习新知
矩形的定义:
有一个角是直角的平行四边形是矩形
探究未知
矩形的角、对角线有什么特殊性呢?
发现一
矩形的四个角都是直角
已知:在矩形ABCD中,∠A=90°
求证: ∠A= ∠B = ∠C= ∠D =90°
验证发现
得出结论
矩形的性质一:
矩形的四个角都是直角
发现二
矩形的对角线相等
推理验证
请同学们小组合作完成第二个发现的数学证明,比一比哪个小组做得最快
得出结论
矩形的性质二:
矩形的对角线相等
【应用新知】
例1 如图,在矩形ABCD中,对角线AC、BD相交于点O,下列说法错误的是( )
【A】∠ABC=90°
【B】AC=BD
【C】OA=OB
【D】OA=AB
【应用新知】
例2 如图,矩形ABCD 对角线AC、BD相交于点O, ∠AOB=60°,AB=4,求矩形对角线的长
一个矩形的一条对角线长为8,两条对角线的一个交角为120°,求这个矩形的边长(保留根号)
【课堂练习】
【课堂小结】
本节课你有哪些收获?
课堂小测
课后作业
教材第53页练习第3题
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
