苏科版八年级下册课件8.2可能性的大小(22张PPT)
文档属性
| 名称 | 苏科版八年级下册课件8.2可能性的大小(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览







文档简介
初二数学:8.2 可能性的大小
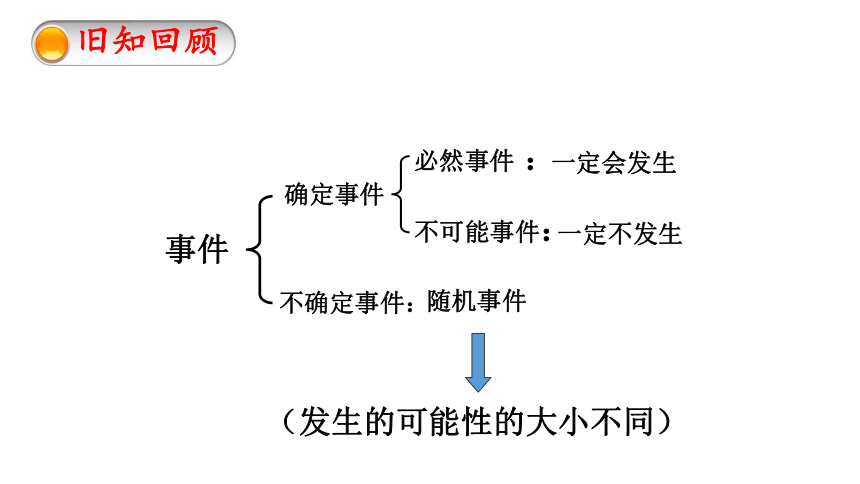
一定会发生
一定不发生
确定事件
必然事件 :
不可能事件:
不确定事件:
随机事件
事件
(发生的可能性的大小不同)
旧知回顾
游戏规则:先请4名同学来做游戏,其中2名同学是同桌关系,他们两人中一人蒙上双眼,其余3人在周围转圈,当中间蒙上双眼的同学喊停时,他手指指向哪位同学,就算找到了这位同学.
在一次游戏中,蒙上双眼的同学一定能找到他的同桌吗?
找
同
桌
新知探究一
1.如图所示,转盘被分成8个相等的扇形.当指针指在哪个颜色的区域上,就说它指向什么颜色.当指针指向边界时,重新转动转盘.
(1) 转动转盘一次,指针会落在哪种颜色的区域上?
(2) 指针落在哪种颜色区域上的可能性大?
(3) 指针落在哪种颜色区域上的可能性小?
新知探究二
(4) 指针会落在黑色区域吗?
黄色或红色或绿色
黄色
绿色
不会,这是一个不可能事件
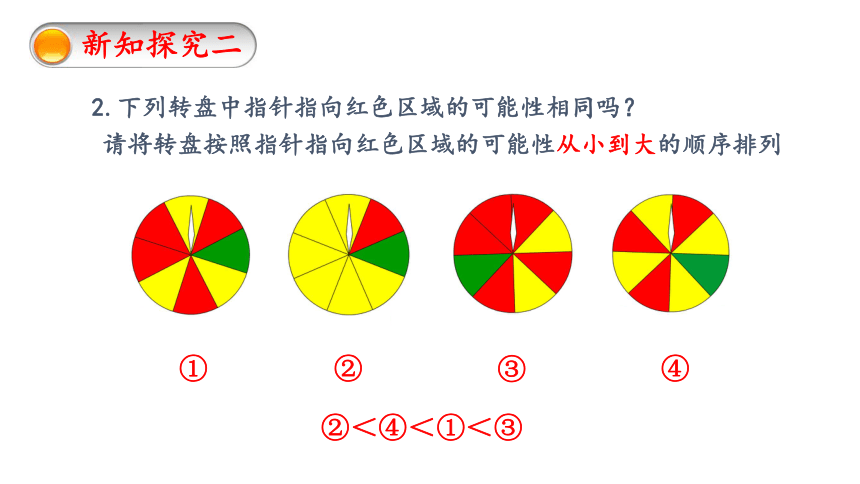
2.下列转盘中指针指向红色区域的可能性相同吗?
请将转盘按照指针指向红色区域的可能性从小到大的顺序排列
学 以 致 用
①
②
③
④
②<④<①<③
新知探究二
6
(1)你认为从中任意摸出1个球,摸到的球可能是哪种颜色?
(3)怎样才能让摸到白球的可能性比红球大呢?
1. 在一个不透明的袋子中装有3个白球和7个红球,每个球除颜色外都相同。
(2)你认为摸到哪种颜色球的可能性大?
(4)怎样才能让摸到白球的可能性更大呢?
(5)摸到白球的可能性与哪些因素有关呢?
新知探究三
可能是白球,可能是红球
摸到红球的可能性大
再多放一些白球或取出一些红球,使白球的数量多于红球的数量
再多放一些白球或取出一些红球,使白球的数量远远多于红球的数量
在摸球试验中,每次摸到的球的颜色是随机的,摸到每个球的可能性是一样的,摸到白球的可能性与白球的数量以及总的球数有关
2.在5个不透明的袋子中分别装有10个球,其中,1号袋中有10个红球,2号袋中有8个红球、2个白球,3号袋中有5个红球、5个白球,4号袋中有1个红球、9个白球,5号袋中有10个白球.
(1) (2) (3) (4) (5)
新知探究三
(1)将球搅匀,分别从每只袋子中任意摸出1个球,摸到白球的可能性一样大吗?为什么?
(2)将袋子的序号按摸到白球的可能性从大到小的顺序排列。
摸到白球的可能性不一样,因为每只袋中白球占总数的比例不同
(5)>(4)>(3)>(2)>(1)
发生的可能性是1
发生的可能性是0
0<发生的可能性<1
新知梳理
例1如图,表示10张扑克牌中的不同情况,任意摸1张,请你说明摸到红色扑克牌的可能性大小,并按可能性从小到大排序.
8.2 可能性的大小
典型例题
[解析] 按每一种情况中红色牌所占的百分比来分析
解: 五种情况中红色牌所占的百分比分别是 A.0%,B.20%,C.50%,D.80%,E.100%,
按可能性从小到大排序为ABCDE.
例2 抛掷一枚均匀的骰子1次,落地后:
(1)朝上的点数会有哪些?它们发生的可能性一样吗?
典型例题
[解析] 因为骰子有6个面,点数分别是1,2,3,4,5,6,所以朝上的点数就有6种可能;
(2)朝上的点数是奇数与朝上的点数是偶数,这两个事件的发生是等可能的吗?
(3)朝上的点数大于4与朝上的点数不大于4,这两个事件的发生是等可能的吗?如是不是可能的,那么哪一个可能性大一些?
[解析] 在1,2,3,4,5,6中有3个奇数、3个偶数,从奇数和偶数所占比例可判断朝上的点数是奇数还是偶数的可能性一样;
[解析] 因为朝上的点数大于4与朝上的点数不大于4所占的比例是1∶2,所以两个事件发生的可能性不一样.
解: 朝上的点数有6种可能,分别是1,2,3,4,5,6,它们发生的可能性是一样的.
解:因为1,2,3,4,5,6中有3个奇数,3个偶数,所以这两个事件的发生是等可能的.
解:不是.朝上的点数大于4与朝上的点数不大于4所占的比例是1∶2,所以朝上的点数大于4发生的可能性小于朝上的点数不大于4发生的可能性.
1.教室里有学号为1-10这十个数的同学,历史老师要随意抽一名同学去默写,会抽到谁呢?
请用“可能”“很可能”“不可能”来填空:
(1)抽到同学的学号_______是10.
(2)抽到同学的学号______小于9.
(3)抽到同学的学号_______是11.
生活中的可能性
可能
很可能
不可能
学以致用
讲 故 事
5 张
唱 歌
3 张
跳 舞
1 张
2.联欢会上有9张卡片,小红可能抽到什么节目?
抽到什么节目的可能性最大?
抽到什么节目的可能性最小?
学 以 致 用
学以致用
答:联欢会上小红可能抽到的节目是讲故事、唱歌或跳舞。
抽到讲故事节目的可能性最大。抽到跳舞的可能性最小。
3.一只小鸟受伤后,落在如图所示操场的哪一块可能性最大( )
A.① B.②
C. ③ D.一样大
②
①
③
学以致用
B
4.某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒。当你随意经过该路口时,遇到哪一种灯的可能性最大?
遇到哪一种灯的可能性最小?根据是什么?
学以致用
答:根据红绿灯亮灯的时间可知:遇到绿灯的可能性最大,遇到黄灯的可能性最小。
5.小明任意买一张电影票(每排有40个座位),座位号是2的倍数与座位号是5的倍数的可能性哪个大?
6.在你们班级任意找2名学生,他们是同一年出生的和同一个月出生的哪一种可能性较大?
学以致用
答: 2的倍数可能性大。
答:同一年出生的可能性大。
学以致用
7.在某校艺体节的兵乓球比赛中,李东顺利进入决赛,且个人技艺高超。某同学预测李东夺冠的可能性是80%,则对该同学的说法理解正确的是( )
A.李东夺冠的可能性较小
B.李东和他的对手比赛10局时,他一定会赢8局
C.李东夺冠的可能性较大
D.李东肯定会赢
C
8.一个纸盒中装有7个红球,2个黄球,1个蓝球,每个球除颜色外完全相同.从中任意摸出一个球.
比较A B C D E五个事件发生的可能性大小,并按可能性从小到大的顺序把它们排列起来.
A :摸出一个球,是红球,或蓝球,或黄球;
B :摸出一个球,是红球;
C :摸出一个球,是黑球;
D :摸出一个球,是蓝球;
E :摸出一个球,是黄球.
C<D<E<B<A
学以致用
9.估计下列事情发生的可能性的大小,将这些事件的序号按照发生的可能性从小到大的顺序排列:
(1)从装有1个红球和2个黄球的袋子中摸出1个白球;
(2)投掷1枚质地均匀的骰子,向上一面的点数是偶数;
(3)调查商场中的1位顾客,他是闰年出生的;
(4)随意调查1位青年,他接受过九年制义务教育;
(5)在地面上抛掷1个小石块,石块会下落.
数学书 P42 :练习1
(1)<(3)<(2)<(4)<(5)
学以致用
8.2 可能性的大小
10. 从一副充分洗过的扑克牌中任取一张,根据下列事件发生的可能性由小到大排序.
(1)抽出的牌是黑色的;
(2)抽出的牌是6;
(3)抽出的牌是黑桃6;
(4)抽出的牌是王;
(5)抽出的牌是梅花.
(3)<(4)<(2)<(5)<(1)
学以致用
常识:一副扑克牌有54张牌,
有4种花色,分别是黑桃,
黑梅花,红桃,红方块,
每个花色各有13张牌,
另外还有大小王各一张。
在一个不透明的袋子中装有仅颜色不同的 10 个小球,其中红球 4 个,黑球 6 个.
(1)先从袋子中取出 m(m>1)个红球,再从袋子中随机摸出 1 个球,将“摸出黑球”记为事件 A.请完成下列表格:
(2)先从袋子中取出 m 个红球,再放入 m 个一样的黑球并摇匀,随机摸出 1 个球是黑球的可能性大小是 ,求 m 的值
4
2或3
巩固提升
巩固提升
解得:m=2
2.必然事件发生的可能性是:1(或100%)
不可能事件发生的可能性是:0
随机事件发生的可能性范围是:0~1
1.一般地,随机事件发生的可能性有大有小.
课堂小结
谢谢同学们!
再见
一定会发生
一定不发生
确定事件
必然事件 :
不可能事件:
不确定事件:
随机事件
事件
(发生的可能性的大小不同)
旧知回顾
游戏规则:先请4名同学来做游戏,其中2名同学是同桌关系,他们两人中一人蒙上双眼,其余3人在周围转圈,当中间蒙上双眼的同学喊停时,他手指指向哪位同学,就算找到了这位同学.
在一次游戏中,蒙上双眼的同学一定能找到他的同桌吗?
找
同
桌
新知探究一
1.如图所示,转盘被分成8个相等的扇形.当指针指在哪个颜色的区域上,就说它指向什么颜色.当指针指向边界时,重新转动转盘.
(1) 转动转盘一次,指针会落在哪种颜色的区域上?
(2) 指针落在哪种颜色区域上的可能性大?
(3) 指针落在哪种颜色区域上的可能性小?
新知探究二
(4) 指针会落在黑色区域吗?
黄色或红色或绿色
黄色
绿色
不会,这是一个不可能事件
2.下列转盘中指针指向红色区域的可能性相同吗?
请将转盘按照指针指向红色区域的可能性从小到大的顺序排列
学 以 致 用
①
②
③
④
②<④<①<③
新知探究二
6
(1)你认为从中任意摸出1个球,摸到的球可能是哪种颜色?
(3)怎样才能让摸到白球的可能性比红球大呢?
1. 在一个不透明的袋子中装有3个白球和7个红球,每个球除颜色外都相同。
(2)你认为摸到哪种颜色球的可能性大?
(4)怎样才能让摸到白球的可能性更大呢?
(5)摸到白球的可能性与哪些因素有关呢?
新知探究三
可能是白球,可能是红球
摸到红球的可能性大
再多放一些白球或取出一些红球,使白球的数量多于红球的数量
再多放一些白球或取出一些红球,使白球的数量远远多于红球的数量
在摸球试验中,每次摸到的球的颜色是随机的,摸到每个球的可能性是一样的,摸到白球的可能性与白球的数量以及总的球数有关
2.在5个不透明的袋子中分别装有10个球,其中,1号袋中有10个红球,2号袋中有8个红球、2个白球,3号袋中有5个红球、5个白球,4号袋中有1个红球、9个白球,5号袋中有10个白球.
(1) (2) (3) (4) (5)
新知探究三
(1)将球搅匀,分别从每只袋子中任意摸出1个球,摸到白球的可能性一样大吗?为什么?
(2)将袋子的序号按摸到白球的可能性从大到小的顺序排列。
摸到白球的可能性不一样,因为每只袋中白球占总数的比例不同
(5)>(4)>(3)>(2)>(1)
发生的可能性是1
发生的可能性是0
0<发生的可能性<1
新知梳理
例1如图,表示10张扑克牌中的不同情况,任意摸1张,请你说明摸到红色扑克牌的可能性大小,并按可能性从小到大排序.
8.2 可能性的大小
典型例题
[解析] 按每一种情况中红色牌所占的百分比来分析
解: 五种情况中红色牌所占的百分比分别是 A.0%,B.20%,C.50%,D.80%,E.100%,
按可能性从小到大排序为ABCDE.
例2 抛掷一枚均匀的骰子1次,落地后:
(1)朝上的点数会有哪些?它们发生的可能性一样吗?
典型例题
[解析] 因为骰子有6个面,点数分别是1,2,3,4,5,6,所以朝上的点数就有6种可能;
(2)朝上的点数是奇数与朝上的点数是偶数,这两个事件的发生是等可能的吗?
(3)朝上的点数大于4与朝上的点数不大于4,这两个事件的发生是等可能的吗?如是不是可能的,那么哪一个可能性大一些?
[解析] 在1,2,3,4,5,6中有3个奇数、3个偶数,从奇数和偶数所占比例可判断朝上的点数是奇数还是偶数的可能性一样;
[解析] 因为朝上的点数大于4与朝上的点数不大于4所占的比例是1∶2,所以两个事件发生的可能性不一样.
解: 朝上的点数有6种可能,分别是1,2,3,4,5,6,它们发生的可能性是一样的.
解:因为1,2,3,4,5,6中有3个奇数,3个偶数,所以这两个事件的发生是等可能的.
解:不是.朝上的点数大于4与朝上的点数不大于4所占的比例是1∶2,所以朝上的点数大于4发生的可能性小于朝上的点数不大于4发生的可能性.
1.教室里有学号为1-10这十个数的同学,历史老师要随意抽一名同学去默写,会抽到谁呢?
请用“可能”“很可能”“不可能”来填空:
(1)抽到同学的学号_______是10.
(2)抽到同学的学号______小于9.
(3)抽到同学的学号_______是11.
生活中的可能性
可能
很可能
不可能
学以致用
讲 故 事
5 张
唱 歌
3 张
跳 舞
1 张
2.联欢会上有9张卡片,小红可能抽到什么节目?
抽到什么节目的可能性最大?
抽到什么节目的可能性最小?
学 以 致 用
学以致用
答:联欢会上小红可能抽到的节目是讲故事、唱歌或跳舞。
抽到讲故事节目的可能性最大。抽到跳舞的可能性最小。
3.一只小鸟受伤后,落在如图所示操场的哪一块可能性最大( )
A.① B.②
C. ③ D.一样大
②
①
③
学以致用
B
4.某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒。当你随意经过该路口时,遇到哪一种灯的可能性最大?
遇到哪一种灯的可能性最小?根据是什么?
学以致用
答:根据红绿灯亮灯的时间可知:遇到绿灯的可能性最大,遇到黄灯的可能性最小。
5.小明任意买一张电影票(每排有40个座位),座位号是2的倍数与座位号是5的倍数的可能性哪个大?
6.在你们班级任意找2名学生,他们是同一年出生的和同一个月出生的哪一种可能性较大?
学以致用
答: 2的倍数可能性大。
答:同一年出生的可能性大。
学以致用
7.在某校艺体节的兵乓球比赛中,李东顺利进入决赛,且个人技艺高超。某同学预测李东夺冠的可能性是80%,则对该同学的说法理解正确的是( )
A.李东夺冠的可能性较小
B.李东和他的对手比赛10局时,他一定会赢8局
C.李东夺冠的可能性较大
D.李东肯定会赢
C
8.一个纸盒中装有7个红球,2个黄球,1个蓝球,每个球除颜色外完全相同.从中任意摸出一个球.
比较A B C D E五个事件发生的可能性大小,并按可能性从小到大的顺序把它们排列起来.
A :摸出一个球,是红球,或蓝球,或黄球;
B :摸出一个球,是红球;
C :摸出一个球,是黑球;
D :摸出一个球,是蓝球;
E :摸出一个球,是黄球.
C<D<E<B<A
学以致用
9.估计下列事情发生的可能性的大小,将这些事件的序号按照发生的可能性从小到大的顺序排列:
(1)从装有1个红球和2个黄球的袋子中摸出1个白球;
(2)投掷1枚质地均匀的骰子,向上一面的点数是偶数;
(3)调查商场中的1位顾客,他是闰年出生的;
(4)随意调查1位青年,他接受过九年制义务教育;
(5)在地面上抛掷1个小石块,石块会下落.
数学书 P42 :练习1
(1)<(3)<(2)<(4)<(5)
学以致用
8.2 可能性的大小
10. 从一副充分洗过的扑克牌中任取一张,根据下列事件发生的可能性由小到大排序.
(1)抽出的牌是黑色的;
(2)抽出的牌是6;
(3)抽出的牌是黑桃6;
(4)抽出的牌是王;
(5)抽出的牌是梅花.
(3)<(4)<(2)<(5)<(1)
学以致用
常识:一副扑克牌有54张牌,
有4种花色,分别是黑桃,
黑梅花,红桃,红方块,
每个花色各有13张牌,
另外还有大小王各一张。
在一个不透明的袋子中装有仅颜色不同的 10 个小球,其中红球 4 个,黑球 6 个.
(1)先从袋子中取出 m(m>1)个红球,再从袋子中随机摸出 1 个球,将“摸出黑球”记为事件 A.请完成下列表格:
(2)先从袋子中取出 m 个红球,再放入 m 个一样的黑球并摇匀,随机摸出 1 个球是黑球的可能性大小是 ,求 m 的值
4
2或3
巩固提升
巩固提升
解得:m=2
2.必然事件发生的可能性是:1(或100%)
不可能事件发生的可能性是:0
随机事件发生的可能性范围是:0~1
1.一般地,随机事件发生的可能性有大有小.
课堂小结
谢谢同学们!
再见
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
