苏科版七年级数学下册 8.3零指数幂与负整数指数幂(共21张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 8.3零指数幂与负整数指数幂(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 10:40:12 | ||
图片预览








文档简介
8.3 零指数幂与负整数指数幂
2.am÷an= (a≠0, m、n都是正 整数,且m>n)
1.同底数幂相除,底数_ ___, 指数____.
不变
相减
am–n
复习:
3.计算:
(1) b2m÷bm-1 (2) (a-b)6÷(b-a)3÷(a-b)2
解: 原式= b2m-(m-1)
= b2m-m+1
= bm+1
解:原式=(b-a)6÷(b-a)3÷(b-a)2
=b-a
=(b-a)6-3-2
学习目标:
1.了解 (a≠0,n为正整数)的
规定;
2.在对“规 定”的合理性做出解释的过程
中,感受从特殊到一般、从具体到抽象的
思考问题的方法。
3.会计算底数为负数的负整数指数幂。
一、阅读教材第55-56页的内容,并完成下列问题
1、计算
53÷53=___
(-3)3÷(-3)3=___
a2÷a2= _(a≠0)
1
1
1
2、思考:
(1)53÷53可以运用同底数幂的除法的运算性质进行计算吗?
可以:53÷53=53-3=50
同理(-3)0 1;a0 1(a≠0)
猜想:50 1
=
= =
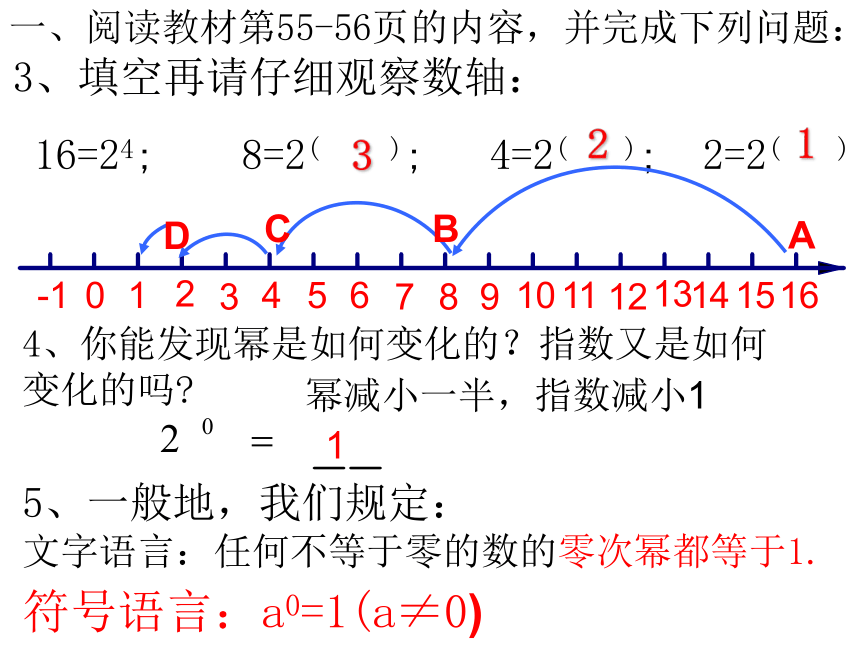
3、填空再请仔细观察数轴:
16=24; 8=2( ); 4=2( ); 2=2( )
3
2
1
4、你能发现幂是如何变化的?指数又是如何变化的吗?
A
B
C
D
一、阅读教材第55-56页的内容,并完成下列问题:
1
5、一般地,我们规定:
文字语言:任何不等于零的数的零次幂都等于1.
符号语言:a0=1(a≠0)
幂减小一半,指数减小1
3
2
1
-1
1
根据同底数幂的除法:
23÷24=23-4=2-1= ;
一、阅读教材第55-56页的内容,并完成下列问题
6、观察式子中指数与幂的变化,你有什么发现?
文字语言:任何不等于0的数的-n(n是正整数)次幂,等于这个数的n次幂的倒数.
7、规定:
=2(0)
=2( )
8=2( )
4=2( )
2=2( )
符号语言: 是正整数
∴ 规定 a0 =1
am–m
am÷am=
=
a0
1
当n是正整数时,
=a0÷a n
=a0–n
=a–n
∴ 规定 :
你能说明理由吗?
am÷am=
一、阅读教材第55-56页的内容,并完成下列问题
二、典型例题
例1:计算:
(1)a5÷a0 (2)a5÷a-2
解法一:(1)a5÷a0
= a5÷1
=a5
(2)a5÷a-2
=a5÷
=a5·a2
=a5+2
=a7
解法二:运用同底数幂的除法运算性质
(1)a5÷a0
= a5-0
=a5
(2)a5÷a-2
=a5-(-2)
=a7
二、典型例题
例2:用小数或分数表示下列各数:
例3:把下列各数写成负整数指数幂的形式
二、典型例题
64=82=43=24
1、判断:下列计算对吗?为什么?错的请改正。
(1)(-7)0= -1
(2 )(-1)0=-1
(3) 00=1
×
(-7)0= 1
×
(-1)0= 1
×
√
2、计算:
解:原式=1—1
=0
三、例题巩固
3、计算
解:原式=0.1+1
=1.1
解:原式
解:原式
解:原式
如何用同底数幂的除法解答题(4)?
方法二:原式
同底数幂的除法运算性质扩展为:
三、例题巩固
1
4
1.5
三、例题巩固
三、例题巩固
解:原式
解:原式
还有其他方法吗?
方
法
二:
原式
三、例题巩固
D
四、拓展延伸
四、拓展延伸
25
26
零和负整数
四、拓展延伸
本节课你的收获是什么?
1.同底幂的除法运算法则:
am÷an=am–n
a0 =1(a≠0)
2.规定 :
小结
(a≠0,m、n为整数)
2020年3月20日数学作业:
一、整理作业:
1、计算:(要有过程)
2、把下列各数写成负整数指数幂的形式
3、用两种方法计算:(要有过程)
4、默写公式:同底数幂的乘法 同底数幂的除法
幂的乘方 积的乘方 零指数幂
负整数指数幂
2020年3月20日数学作业:
二、练习作业:
2、书57页 “练一练”及59页习题8.3 第3、4两题(要求:有过程);
3、小本同底数幂的除法1(28--30页)、大本同底数幂的除法1(31页)(要求:有过程);
4、全品 同底数幂的除法(27页)(要求:有过程)。
注意晚上发答案,自我红笔订正,后写名字,拍照,上传至微信小程序。(上传的作业按发作业的顺序上传)
2.am÷an= (a≠0, m、n都是正 整数,且m>n)
1.同底数幂相除,底数_ ___, 指数____.
不变
相减
am–n
复习:
3.计算:
(1) b2m÷bm-1 (2) (a-b)6÷(b-a)3÷(a-b)2
解: 原式= b2m-(m-1)
= b2m-m+1
= bm+1
解:原式=(b-a)6÷(b-a)3÷(b-a)2
=b-a
=(b-a)6-3-2
学习目标:
1.了解 (a≠0,n为正整数)的
规定;
2.在对“规 定”的合理性做出解释的过程
中,感受从特殊到一般、从具体到抽象的
思考问题的方法。
3.会计算底数为负数的负整数指数幂。
一、阅读教材第55-56页的内容,并完成下列问题
1、计算
53÷53=___
(-3)3÷(-3)3=___
a2÷a2= _(a≠0)
1
1
1
2、思考:
(1)53÷53可以运用同底数幂的除法的运算性质进行计算吗?
可以:53÷53=53-3=50
同理(-3)0 1;a0 1(a≠0)
猜想:50 1
=
= =
3、填空再请仔细观察数轴:
16=24; 8=2( ); 4=2( ); 2=2( )
3
2
1
4、你能发现幂是如何变化的?指数又是如何变化的吗?
A
B
C
D
一、阅读教材第55-56页的内容,并完成下列问题:
1
5、一般地,我们规定:
文字语言:任何不等于零的数的零次幂都等于1.
符号语言:a0=1(a≠0)
幂减小一半,指数减小1
3
2
1
-1
1
根据同底数幂的除法:
23÷24=23-4=2-1= ;
一、阅读教材第55-56页的内容,并完成下列问题
6、观察式子中指数与幂的变化,你有什么发现?
文字语言:任何不等于0的数的-n(n是正整数)次幂,等于这个数的n次幂的倒数.
7、规定:
=2(0)
=2( )
8=2( )
4=2( )
2=2( )
符号语言: 是正整数
∴ 规定 a0 =1
am–m
am÷am=
=
a0
1
当n是正整数时,
=a0÷a n
=a0–n
=a–n
∴ 规定 :
你能说明理由吗?
am÷am=
一、阅读教材第55-56页的内容,并完成下列问题
二、典型例题
例1:计算:
(1)a5÷a0 (2)a5÷a-2
解法一:(1)a5÷a0
= a5÷1
=a5
(2)a5÷a-2
=a5÷
=a5·a2
=a5+2
=a7
解法二:运用同底数幂的除法运算性质
(1)a5÷a0
= a5-0
=a5
(2)a5÷a-2
=a5-(-2)
=a7
二、典型例题
例2:用小数或分数表示下列各数:
例3:把下列各数写成负整数指数幂的形式
二、典型例题
64=82=43=24
1、判断:下列计算对吗?为什么?错的请改正。
(1)(-7)0= -1
(2 )(-1)0=-1
(3) 00=1
×
(-7)0= 1
×
(-1)0= 1
×
√
2、计算:
解:原式=1—1
=0
三、例题巩固
3、计算
解:原式=0.1+1
=1.1
解:原式
解:原式
解:原式
如何用同底数幂的除法解答题(4)?
方法二:原式
同底数幂的除法运算性质扩展为:
三、例题巩固
1
4
1.5
三、例题巩固
三、例题巩固
解:原式
解:原式
还有其他方法吗?
方
法
二:
原式
三、例题巩固
D
四、拓展延伸
四、拓展延伸
25
26
零和负整数
四、拓展延伸
本节课你的收获是什么?
1.同底幂的除法运算法则:
am÷an=am–n
a0 =1(a≠0)
2.规定 :
小结
(a≠0,m、n为整数)
2020年3月20日数学作业:
一、整理作业:
1、计算:(要有过程)
2、把下列各数写成负整数指数幂的形式
3、用两种方法计算:(要有过程)
4、默写公式:同底数幂的乘法 同底数幂的除法
幂的乘方 积的乘方 零指数幂
负整数指数幂
2020年3月20日数学作业:
二、练习作业:
2、书57页 “练一练”及59页习题8.3 第3、4两题(要求:有过程);
3、小本同底数幂的除法1(28--30页)、大本同底数幂的除法1(31页)(要求:有过程);
4、全品 同底数幂的除法(27页)(要求:有过程)。
注意晚上发答案,自我红笔订正,后写名字,拍照,上传至微信小程序。(上传的作业按发作业的顺序上传)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
