苏科版七年级数学下册 7.5多边形的内角和与外角和3 课件(16ppt)
文档属性
| 名称 | 苏科版七年级数学下册 7.5多边形的内角和与外角和3 课件(16ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 348.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览






文档简介
7.5多边形的内角和与外角和(3)
数学不是看出来的,也不是想出来的,而是做出来的。
学习目标:
经历操作、计算,认识多边形的外角;利用三角形的外角和,探索多边形的外角和是360°,并能进行简单的应用;体会从一般到特殊再到一般的过程。
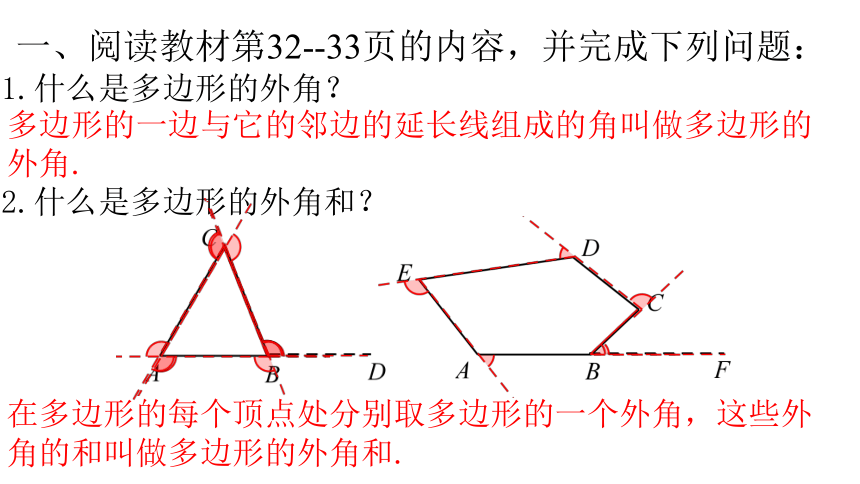
1.什么是多边形的外角?
2.什么是多边形的外角和?
多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.
在多边形的每个顶点处分别取多边形的一个外角,这些外角的和叫做多边形的外角和.
一、阅读教材第32--33页的内容,并完成下列问题:
3.三角形的外角和是_______°
360°
一、阅读教材第32--33页的内容,并完成下列问题:
4.四边形的外角和是_______°
360°
一、阅读教材第32--33页的内容,并完成下列问题:
解:∠α、∠β、∠γ、∠δ是四边形ABCD的4个外角
∠α+∠1=180°,
∠β+∠2=180°
∠γ+∠3=180°
∠δ+∠4=180°,
∠1+∠2+∠3+∠4=180°×2,
则∠α+∠β+∠γ+∠δ= 。
180°×4-180°×2=360°
5.五边形的外角和是_ ______°
六边形的外角和是__ _____°
n边形的外角和是____ ___
一、阅读教材第32--33页的内容,并完成下列问题:
180°·n-(n-2)·180°=360°
180°×5-180°×(5-2)=360°
180°×6-180°×(6-2)=360°
例1 填空题:
七边形的外角和为______;
360°
二、典型例题:
变式一:若一个多边形的每个外角都是72°,这是_____边形;
五
方法一:72°·n=360°
方法二:每个外角都是72°,则每个内角是:
180°-72°=108°。
则(n-2)·180°=108°·n
得:n=5
二、典型例题:
变式二:若一个多边形的内角和比它的外角和的3倍少180°,
求这个多变形的边数和内角和
解:设这个多边形是n边形,则内角和是:(n-2)·180°
外角和是:360°。
由题意可得:
(n-2)·180°=360°×3-180°
得:n=7
所以这个多边形的内角和是:(7-2)×180°=900°
例2.多边形边数增加一条,它的内角和增加 ,
外角和 。
二、典型例题:
180°
不变,还是360°
例3.如图,在△ABC中,∠A=27°,∠B=48°,∠ACD是△ABC的一个外角,则∠ACD等于( )
A.75° B.80° C.105° D.54°
∠A+∠B=180°-∠ACB
∠ACD=180°-∠ACB
A
∠ACD=∠A+∠B
二、典型例题:
总结:三角形的一个外角等于 。
与它不相邻的两个内角的和
变式:求下列的角度。
x= x= y= 。
47° 50° 140°
x°+(x-10)°=90°(
1.一个多边形的每一个内角都是120°,这个多边形是 边形,它的内角和等于 度。
三、例题巩固:
六
720
2.一个多边形的内角和与外角和的总和为1800°,这个多边形是 边数.
10
解:设这个多边形是n边形,则内角和是:(n-2)·180°
外角和是:360°。
由题意可得:
(n-2)·180°+360°=1800°
得:n=10
3.如图,小华从点A出发,沿直线前进10 m后向左转20°,再沿直线前进10 m,又向左转20°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是( )
A.200 m B.180 m
C.160 m D.140 m
B
360°÷20°=18(
三、例题巩固:
从图中的五边形ABCDE纸片中剪去一个三角形,剩余部分是几边形?它们的内角和、外角和分别是多少?
四边形,内角和360°,外角和360°
五边形,内角和540°,外角和360°
六边形,内角和720°,外角和360°
四、拓展延伸:
1. 什么是多边形的外角?
2. 多边形的外角和等于多少?
3. 如何求正多边形的每一个内角和外角?
你有何收获?
数学不是看出来的,也不是想出来的,而是做出来的。
学习目标:
经历操作、计算,认识多边形的外角;利用三角形的外角和,探索多边形的外角和是360°,并能进行简单的应用;体会从一般到特殊再到一般的过程。
1.什么是多边形的外角?
2.什么是多边形的外角和?
多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.
在多边形的每个顶点处分别取多边形的一个外角,这些外角的和叫做多边形的外角和.
一、阅读教材第32--33页的内容,并完成下列问题:
3.三角形的外角和是_______°
360°
一、阅读教材第32--33页的内容,并完成下列问题:
4.四边形的外角和是_______°
360°
一、阅读教材第32--33页的内容,并完成下列问题:
解:∠α、∠β、∠γ、∠δ是四边形ABCD的4个外角
∠α+∠1=180°,
∠β+∠2=180°
∠γ+∠3=180°
∠δ+∠4=180°,
∠1+∠2+∠3+∠4=180°×2,
则∠α+∠β+∠γ+∠δ= 。
180°×4-180°×2=360°
5.五边形的外角和是_ ______°
六边形的外角和是__ _____°
n边形的外角和是____ ___
一、阅读教材第32--33页的内容,并完成下列问题:
180°·n-(n-2)·180°=360°
180°×5-180°×(5-2)=360°
180°×6-180°×(6-2)=360°
例1 填空题:
七边形的外角和为______;
360°
二、典型例题:
变式一:若一个多边形的每个外角都是72°,这是_____边形;
五
方法一:72°·n=360°
方法二:每个外角都是72°,则每个内角是:
180°-72°=108°。
则(n-2)·180°=108°·n
得:n=5
二、典型例题:
变式二:若一个多边形的内角和比它的外角和的3倍少180°,
求这个多变形的边数和内角和
解:设这个多边形是n边形,则内角和是:(n-2)·180°
外角和是:360°。
由题意可得:
(n-2)·180°=360°×3-180°
得:n=7
所以这个多边形的内角和是:(7-2)×180°=900°
例2.多边形边数增加一条,它的内角和增加 ,
外角和 。
二、典型例题:
180°
不变,还是360°
例3.如图,在△ABC中,∠A=27°,∠B=48°,∠ACD是△ABC的一个外角,则∠ACD等于( )
A.75° B.80° C.105° D.54°
∠A+∠B=180°-∠ACB
∠ACD=180°-∠ACB
A
∠ACD=∠A+∠B
二、典型例题:
总结:三角形的一个外角等于 。
与它不相邻的两个内角的和
变式:求下列的角度。
x= x= y= 。
47° 50° 140°
x°+(x-10)°=90°(
1.一个多边形的每一个内角都是120°,这个多边形是 边形,它的内角和等于 度。
三、例题巩固:
六
720
2.一个多边形的内角和与外角和的总和为1800°,这个多边形是 边数.
10
解:设这个多边形是n边形,则内角和是:(n-2)·180°
外角和是:360°。
由题意可得:
(n-2)·180°+360°=1800°
得:n=10
3.如图,小华从点A出发,沿直线前进10 m后向左转20°,再沿直线前进10 m,又向左转20°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是( )
A.200 m B.180 m
C.160 m D.140 m
B
360°÷20°=18(
三、例题巩固:
从图中的五边形ABCDE纸片中剪去一个三角形,剩余部分是几边形?它们的内角和、外角和分别是多少?
四边形,内角和360°,外角和360°
五边形,内角和540°,外角和360°
六边形,内角和720°,外角和360°
四、拓展延伸:
1. 什么是多边形的外角?
2. 多边形的外角和等于多少?
3. 如何求正多边形的每一个内角和外角?
你有何收获?
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
