苏科版七年级数学下册8.2:幂的乘方与积的乘方(2)课件 (共27张PPT)
文档属性
| 名称 | 苏科版七年级数学下册8.2:幂的乘方与积的乘方(2)课件 (共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 752.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 10:32:15 | ||
图片预览








文档简介
知识回顾
填空:
1. 3am+am=_____,依据 .
2. a3·a6=____,依据 .
3. (a4)3=_____,依据 .
4. (m4)2+m5·m3= ,(a3)5·(a2)2= .
5. 若am=3,an=2,则am+2n= .
4am
合并同类项法则
a9
同底数幂乘法的运算性质
12
a12
幂的乘方的运算性质
2m8
a19
8.2 幂的乘方与积的乘方(1)
苏科版七年级下册
比一比
⑴ (1×2)4=____; 14×24 =_____;
⑵ [3×(-2)]3=_____; 33×(-2)3=_____;
⑶ ( )2= ; = .
16
16
-216
-216
你发现了什么?
填空:
1
(ab)n= .
anbn
(n为正整数)
(ab)n=_____.(n为正整数)
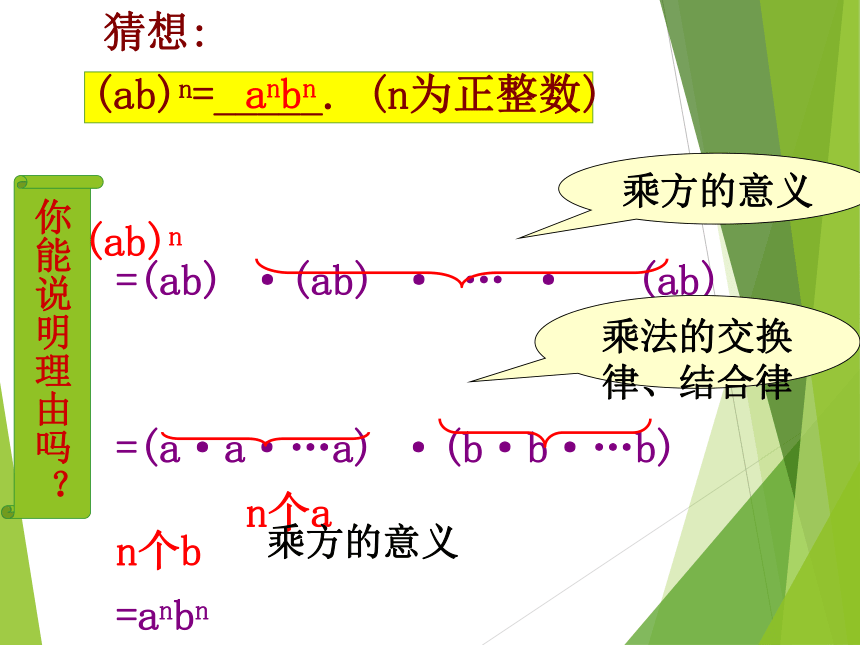
猜想:
你能说明理由吗?
=(ab) ·(ab) · … · (ab)
n个ab
=(a·a·…a) ·(b·b·…b)
n个a n个b
=anbn
(ab)n
乘方的意义
乘法的交换律、结合律
乘方的意义
(ab)n=_____. (n为正整数)
anbn
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
你能用文字语言叙述这个性质吗?
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
例1. 计算:
(1) (5m)3 (2) (3×103)2
解:原式
解:原式
1.计算:
(1) (-ab)5 (2) (x2y3)4
(3) (4×103)2 (4) (-3a3)3
×
×
x3
4
2.下面的计算是否正确?如果有错误,请改正.
(1) (xy2)3= x y6 ( )
(2) (-2b2)2=-4 b4 ( )
3.在括号里填写适当的计算依据:
(1)[(3x)2]3
=(3x)6 ( )
=36x6 ( )
=729x6 ( )
(2)[(3x)2]3
=(9x2)3 ( )
=93(x2)3 ( )
=729x6 ( )
积的乘方的运算性质
积的乘方的运算性质
积的乘方的运算性质
幂的乘方的运算性质
幂的乘方的运算性质
幂的乘方的运算性质
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
请你推广:
(abc)n =
anbncn
(n为正整数)
(abc)n
=[(ab)c]n
=anbncn
=(ab)ncn
1
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
(abc)n =
anbncn
(n为正整数)
请你推广:
(abc)n
=[(ab)c]n
=anbncn
=(ab)ncn
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
1
(abc)n =
anbncn
(n为正整数)
例2 . 计算:
(1)(3xy2)2 (2) (-2ab3c2)4
解:原式
解:原式
1.计算:
(1) (-3x2y)3 (2) (-5ab)2
(3) (2xnym)2 (4) (-2xy2z3)4
2.计算:
⑴ (-a2)3.(-a3)2 ⑵ (-n)2.(-n5)3
⑶ a5.a3+(2a2)4 ⑷ (-2a)3-(-a).a2
例3.一个圆柱形的储油罐内壁半径r是 20m,高h是40m.如果该储油罐最大储油高度为30m,最多能储油多少L?(1m3 =103 L)
40m
20m
解:V=
≈3.14×(2×10)2×(3×10)
=3.14×(4×102)×(3×10)
=3.14×12×103
≈ 3.8×104m3
=3.8×107L
答:储油罐的容积是3.8×107L.
=1
6个
6个2
解:原式
你会计算吗?
拓展延伸
拓展延伸
逆用积的乘方的运算性质
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
你会计算吗?
解:原式
=1
练一练
计算:
(1)0.255×45
(2)
解:原式
幂的乘方的运算性质
逆用同底数幂的乘法运算性质
逆用积的乘方的运算性质
拓展延伸
【当堂反馈】
课堂小结
1.积的乘方公式与法则:
(1)公式: ;
(2)法则:积的乘方,把积的每一个____分别_____,再把___________;
(3) 推广: .
2.积的乘方公式的逆用: .
因式
乘方
所得的幂相乘
anbn=(ab)n(n为正整数)
(abc)n=anbncn(n为正整数)
(ab)n=anbn(n为正整数)
回顾与思考
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算性质:
am · an
=
am+n
(m,n都是正整数)
幂的乘方运算性质:
(am)n=
amn(m、n都是正整数)
积的乘方运算性质:
(ab)n=anbn
(m、n都是正整数)
逆向使用
am · an =am+n
(am)n =amn
an·bn = (ab)n
可使某些计算简捷。
提醒:
课后作业:补充习题
填空:
1. 3am+am=_____,依据 .
2. a3·a6=____,依据 .
3. (a4)3=_____,依据 .
4. (m4)2+m5·m3= ,(a3)5·(a2)2= .
5. 若am=3,an=2,则am+2n= .
4am
合并同类项法则
a9
同底数幂乘法的运算性质
12
a12
幂的乘方的运算性质
2m8
a19
8.2 幂的乘方与积的乘方(1)
苏科版七年级下册
比一比
⑴ (1×2)4=____; 14×24 =_____;
⑵ [3×(-2)]3=_____; 33×(-2)3=_____;
⑶ ( )2= ; = .
16
16
-216
-216
你发现了什么?
填空:
1
(ab)n= .
anbn
(n为正整数)
(ab)n=_____.(n为正整数)
猜想:
你能说明理由吗?
=(ab) ·(ab) · … · (ab)
n个ab
=(a·a·…a) ·(b·b·…b)
n个a n个b
=anbn
(ab)n
乘方的意义
乘法的交换律、结合律
乘方的意义
(ab)n=_____. (n为正整数)
anbn
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
你能用文字语言叙述这个性质吗?
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘.
例1. 计算:
(1) (5m)3 (2) (3×103)2
解:原式
解:原式
1.计算:
(1) (-ab)5 (2) (x2y3)4
(3) (4×103)2 (4) (-3a3)3
×
×
x3
4
2.下面的计算是否正确?如果有错误,请改正.
(1) (xy2)3= x y6 ( )
(2) (-2b2)2=-4 b4 ( )
3.在括号里填写适当的计算依据:
(1)[(3x)2]3
=(3x)6 ( )
=36x6 ( )
=729x6 ( )
(2)[(3x)2]3
=(9x2)3 ( )
=93(x2)3 ( )
=729x6 ( )
积的乘方的运算性质
积的乘方的运算性质
积的乘方的运算性质
幂的乘方的运算性质
幂的乘方的运算性质
幂的乘方的运算性质
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
请你推广:
(abc)n =
anbncn
(n为正整数)
(abc)n
=[(ab)c]n
=anbncn
=(ab)ncn
1
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
(abc)n =
anbncn
(n为正整数)
请你推广:
(abc)n
=[(ab)c]n
=anbncn
=(ab)ncn
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
1
(abc)n =
anbncn
(n为正整数)
例2 . 计算:
(1)(3xy2)2 (2) (-2ab3c2)4
解:原式
解:原式
1.计算:
(1) (-3x2y)3 (2) (-5ab)2
(3) (2xnym)2 (4) (-2xy2z3)4
2.计算:
⑴ (-a2)3.(-a3)2 ⑵ (-n)2.(-n5)3
⑶ a5.a3+(2a2)4 ⑷ (-2a)3-(-a).a2
例3.一个圆柱形的储油罐内壁半径r是 20m,高h是40m.如果该储油罐最大储油高度为30m,最多能储油多少L?(1m3 =103 L)
40m
20m
解:V=
≈3.14×(2×10)2×(3×10)
=3.14×(4×102)×(3×10)
=3.14×12×103
≈ 3.8×104m3
=3.8×107L
答:储油罐的容积是3.8×107L.
=1
6个
6个2
解:原式
你会计算吗?
拓展延伸
拓展延伸
逆用积的乘方的运算性质
积的乘方的运算性质:
(ab)n=_____.(n为正整数)
(ab)n=_____. (n为正整数)
anbn
你会计算吗?
解:原式
=1
练一练
计算:
(1)0.255×45
(2)
解:原式
幂的乘方的运算性质
逆用同底数幂的乘法运算性质
逆用积的乘方的运算性质
拓展延伸
【当堂反馈】
课堂小结
1.积的乘方公式与法则:
(1)公式: ;
(2)法则:积的乘方,把积的每一个____分别_____,再把___________;
(3) 推广: .
2.积的乘方公式的逆用: .
因式
乘方
所得的幂相乘
anbn=(ab)n(n为正整数)
(abc)n=anbncn(n为正整数)
(ab)n=anbn(n为正整数)
回顾与思考
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算性质:
am · an
=
am+n
(m,n都是正整数)
幂的乘方运算性质:
(am)n=
amn(m、n都是正整数)
积的乘方运算性质:
(ab)n=anbn
(m、n都是正整数)
逆向使用
am · an =am+n
(am)n =amn
an·bn = (ab)n
可使某些计算简捷。
提醒:
课后作业:补充习题
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
