苏科版七年级下册数学:第11章 一元一次不等式 小结与思考(共19张PPT)
文档属性
| 名称 | 苏科版七年级下册数学:第11章 一元一次不等式 小结与思考(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 792.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
苏科版七年级下册
一元一次不等式复习
从实际问题感受这一章知识设计思路
实际问题:如图是小明测量一颗玻璃球体积的过程:
(1)将300 的水倒进一个容量为500 的杯子中;
(2)将四颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.根据以上过程,你能推测这样一颗玻璃球的体积在什么范围内吗?
解:设一颗小球的体积为x
由题意得:
<200
>200
解这个不等式得:40<x<50
答:一颗玻璃球的体积大于40 且小于50
通过实际问题的分析、
解决过程,你能感受
到这一章知识结构设
计思路吗?
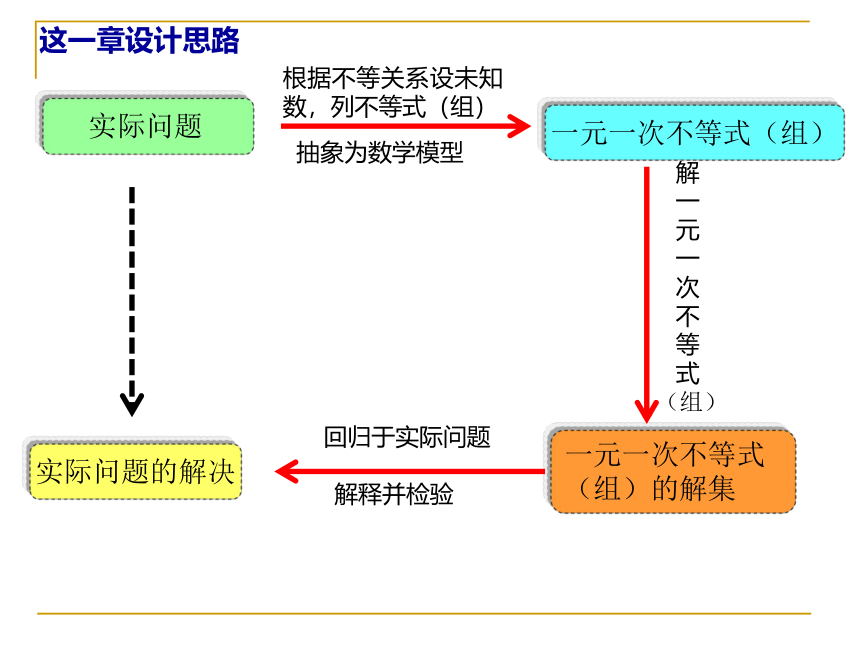
实际问题
一元一次不等式(组)
一元一次不等式
(组)的解集
实际问题的解决
根据不等关系设未知数,列不等式(组)
抽象为数学模型
回归于实际问题
解释并检验
解
一
元
一
次
不
等
式
(组)
这一章设计思路
重温知识,建构知识体系
题目
题目涉及的主要知识或方法
1、根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t(℃),表示t和6000之间的关系:___________
t ≥ 6000
3、x与y的和不大于6,由此可得不等式:____________
x+y≤6
4、a与b的差是非负数:________
2、小明的月工资至多3000元:设小明的月工资为x元,表示x与3000的关系:__________
5、y与5的和小于-4:________
a-b≥0
y+5<-4
1、不等式的概念:用不等号表示不等关系的式子叫不等式 (不等号: >、<、≠、≤、≥)
2、列不等式的关键:
抓住关键词
大于 (高出、超过)
小于 (不足、低于)
不大于(不超过、至多)
不小于(不低于、至少)
正数、负数、非负数、非正数
x≤3000
重温知识,建构知识体系
题目
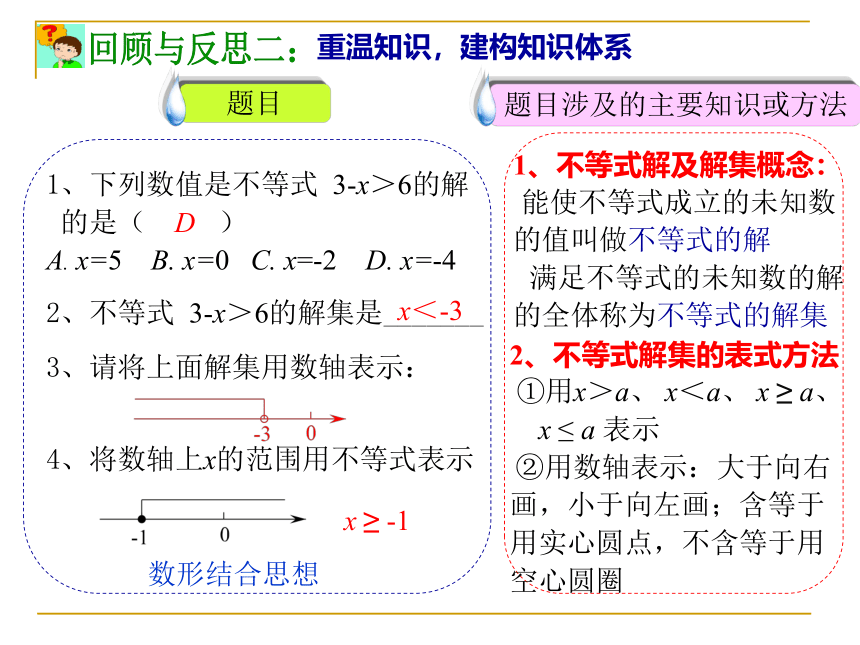
1、下列数值是不等式 3-x>6的解
的是( )
A. x=5 B. x=0 C. x=-2 D. x=-4
2、不等式 3-x>6的解集是_______
3、请将上面解集用数轴表示:
4、将数轴上x的范围用不等式表示
x<-3
D
x ≥ -1
1、不等式解及解集概念:
能使不等式成立的未知数的值叫做不等式的解
满足不等式的未知数的解的全体称为不等式的解集
2、不等式解集的表式方法
①用x>a、 x<a、 x ≥ a、
x ≤ a 表示
②用数轴表示:大于向右画,小于向左画;含等于用实心圆点,不含等于用空心圆圈
题目涉及的主要知识或方法
数形结合思想
重温知识,建构知识体系
题目
1、已知a<b,下列式子中,错误的是( )
A. 4a<4b B. -4a<-4b
C. a+4<b+4 D. a-4<b-4
3、若x>y,则ax>ay.那么一定有
( )
a>0 B. a≥0
C. a<0 D. a≤0
2、已知
,用不等号连接
B
<
A
1、不等式的基本性质
不等式性质①:不等式
两边都加上 (或减去)同一个数(或同一个整式),不等号方向不变
不等式性质②:不等式两边都乘以 (或除以)同一个正数,不等号方向不变
不等式两边都乘以 (或除以)同一个负数,不等号方向改变
题目涉及的主要知识或方法
重温知识,建构知识体系
题目
1、已知 >2是关于x的一元一次不等式,则a =_____,不等式的解集为________
2
x>0
1、一元一次不等式概念:只含有一个未知数,并且未知数的次数都是1,系数不为0
题目涉及的主要知识或方法
重温知识,建构知识体系
题目
1、求不等式解集
解:去分母得:
>
x>1
>
去括号得:
移项得:
>
合并同类项得:
>
系数化为1得:
1、解不等式的一般步骤:去分母、去括号、移项、
合并同类项、系数化为1
2、解不等式要注意的细节:①利用不等式性质2时,注意是否需要改变不等号的方向
②去分母时,左右两边每一项都要乘,如果分子为多项式,一定要将多项式加上括号,
题目涉及的主要知识或方法
重温知识,建构知识体系
题目
1、求不等式组 的解集
≤0 ①
>0 ②
解:解不等式①得:x≤1
解不等式②得:x>-2
∴不等式组的解集为:-2<x≤1
2、你能直接说出下列不等式组的解
集吗
1、不等式组的概念
2、不等组的解集:不等式组中所有不等式的解集的公共部分
3、确定不等式组解集的方法:
①利用数轴:
②利用法则:
同大取大, 同小取小,
大于小的,小于大的,中间找 大于大的,小于小的,找不了
直观形象
方便快捷
题目涉及的主要知识或方法
建构本章知识体系
一
元
一
次
不
等
式
不等式
一元一次不等式
一元一次不等式组
不等式定义
不等式性质
一元一次不等式应用
不等式解集及表示方法
一元一次不等式定义
一元一次不等式解法
一元一次不等式组的定义
一元一次不等式组的解法
特殊化
组成
一
元
一
次
方
程
二
元
一
次
方
程
(组)
类比
学习
感受二元一次方程与一元一次方程、一元一次不等式(组)之间的关系
1、已知
题目
感受彼此关系
①若x=1时,则y=________
②若-4≤y<1时,则x的取值
范围_____________
①、当二元一次方程中的一个未知数取值确定时,二元一次方程就转化成一元一次方程,从而求出另一个未知数值
解:由2x+y=6得y=6-2x
∵ -4≤y<1
∴-4≤6-2x<1
解这个不等式组得:
<x≤5
②、当二元一次方程中的一个未知数取值范围确定时,可利用一元一次不等式(组)确定另一个未知数的取值范围
4
典例剖析
求不等式 的非正整数解.
解不等式,得x>-4,
解:
所以非正整数解是:-3,-2,-1,0 .
解题思路指导:
求不等式(组)特殊解时,一般先求出不等式(组)的解集,然后在解集范围内找出特殊解,必要时可借助于数轴,形象直观
典例剖析
解:
解题思路指导:
先求出方程(组)的解,即用k的代数式表示x、y;然后再列出k的不等式(组),最后解关于k的不等式(组)
如果关于x、y的方程组
的解满足条件
,求k的取值范围。
①+②得:5x+5y=k+4
∵0<x+y<1
∴0< <1
解不等式组得:-4<k<1
整体思想
请你静心反思,通过对本章内容的复习,你有哪些新的收获?把你的新认识与周围的伙伴们一起分享吧!
反思与分享
1、知识储备:①如果ab>0,那么_________________
如果ab<0,那么_________________
②如果 >0,那么________________
如果 <0,那么_________________
拓展与延伸
知识运用:请你尝试求下列不等式解集
<0
>0
a>0
b>0
a<0
b<0
或
a>0
b<0
a<0
b>0
或
a>0
b>0
a<0
b<0
或
a>0
b<0
a<0
b>0
或
解题思路指导:
<0
解:
∵
<0
∴ (1)
3x+6>0
2x-2<0
3x+6<0
2x-2>0
或(2)
解不等式组(1)得:-2< x<1
不等式组(2)无解
∴原不等式的解集为-2<x<1
利用除法法则进行分类讨论,从而解决问题
拓展与延伸
>0
解:
拓展与延伸
∵
>0
∴ x(x-3) >0
∴ (1)
x>0
x-3>0
x<0
x-3<0
或(2)
解不等式组(1)得:x>3
解不等式组(2)得:x<0
∴原不等式的解集为x>3或x<0
解题思路指导:
对不等式左边多项式因式分解,再利用乘法法则,将一元二次不等式转化为一元一次不等式
28.(本题满分10分) 小明家需要用钢管做防盗窗,按设计要求,其中需要长为0.8m,2.5m且粗细相同的钢管分别为100根,32根,并要求这些用料不能是焊接而成的.现钢材市场的这种规格的钢管每根为6m.
(1)试问一根6米长的钢管有哪些裁剪方法呢 请填写下空(余料作废).
方法1:当只裁剪长为0.8米的用料时,最多可剪 ▲ 根;
方法2:当先剪下1根2.5米的用料时,余下部分最多能剪0.8米长的用料 ▲ 根:
方法3:当先剪下 2根2.5米的用料时,余下部分最多能剪0.8米长的用料 ▲ 根.
(2)联合用(1)中的方法2和方法3各裁剪多少根6米长的钢管,才能刚好得到所需要的相应数量的材料
(3)小明经过探究发现:如果联合(1)中的二种或三种裁剪方法,还有多种方案能刚好得到所需要的相应数量的材料,并且所需要6m长的钢管与(2)中根数相同,试帮小明说明理由,并写出一种与(2)不同的裁剪方案.
苏科版七年级下册
一元一次不等式复习
从实际问题感受这一章知识设计思路
实际问题:如图是小明测量一颗玻璃球体积的过程:
(1)将300 的水倒进一个容量为500 的杯子中;
(2)将四颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.根据以上过程,你能推测这样一颗玻璃球的体积在什么范围内吗?
解:设一颗小球的体积为x
由题意得:
<200
>200
解这个不等式得:40<x<50
答:一颗玻璃球的体积大于40 且小于50
通过实际问题的分析、
解决过程,你能感受
到这一章知识结构设
计思路吗?
实际问题
一元一次不等式(组)
一元一次不等式
(组)的解集
实际问题的解决
根据不等关系设未知数,列不等式(组)
抽象为数学模型
回归于实际问题
解释并检验
解
一
元
一
次
不
等
式
(组)
这一章设计思路
重温知识,建构知识体系
题目
题目涉及的主要知识或方法
1、根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t(℃),表示t和6000之间的关系:___________
t ≥ 6000
3、x与y的和不大于6,由此可得不等式:____________
x+y≤6
4、a与b的差是非负数:________
2、小明的月工资至多3000元:设小明的月工资为x元,表示x与3000的关系:__________
5、y与5的和小于-4:________
a-b≥0
y+5<-4
1、不等式的概念:用不等号表示不等关系的式子叫不等式 (不等号: >、<、≠、≤、≥)
2、列不等式的关键:
抓住关键词
大于 (高出、超过)
小于 (不足、低于)
不大于(不超过、至多)
不小于(不低于、至少)
正数、负数、非负数、非正数
x≤3000
重温知识,建构知识体系
题目
1、下列数值是不等式 3-x>6的解
的是( )
A. x=5 B. x=0 C. x=-2 D. x=-4
2、不等式 3-x>6的解集是_______
3、请将上面解集用数轴表示:
4、将数轴上x的范围用不等式表示
x<-3
D
x ≥ -1
1、不等式解及解集概念:
能使不等式成立的未知数的值叫做不等式的解
满足不等式的未知数的解的全体称为不等式的解集
2、不等式解集的表式方法
①用x>a、 x<a、 x ≥ a、
x ≤ a 表示
②用数轴表示:大于向右画,小于向左画;含等于用实心圆点,不含等于用空心圆圈
题目涉及的主要知识或方法
数形结合思想
重温知识,建构知识体系
题目
1、已知a<b,下列式子中,错误的是( )
A. 4a<4b B. -4a<-4b
C. a+4<b+4 D. a-4<b-4
3、若x>y,则ax>ay.那么一定有
( )
a>0 B. a≥0
C. a<0 D. a≤0
2、已知
,用不等号连接
B
<
A
1、不等式的基本性质
不等式性质①:不等式
两边都加上 (或减去)同一个数(或同一个整式),不等号方向不变
不等式性质②:不等式两边都乘以 (或除以)同一个正数,不等号方向不变
不等式两边都乘以 (或除以)同一个负数,不等号方向改变
题目涉及的主要知识或方法
重温知识,建构知识体系
题目
1、已知 >2是关于x的一元一次不等式,则a =_____,不等式的解集为________
2
x>0
1、一元一次不等式概念:只含有一个未知数,并且未知数的次数都是1,系数不为0
题目涉及的主要知识或方法
重温知识,建构知识体系
题目
1、求不等式解集
解:去分母得:
>
x>1
>
去括号得:
移项得:
>
合并同类项得:
>
系数化为1得:
1、解不等式的一般步骤:去分母、去括号、移项、
合并同类项、系数化为1
2、解不等式要注意的细节:①利用不等式性质2时,注意是否需要改变不等号的方向
②去分母时,左右两边每一项都要乘,如果分子为多项式,一定要将多项式加上括号,
题目涉及的主要知识或方法
重温知识,建构知识体系
题目
1、求不等式组 的解集
≤0 ①
>0 ②
解:解不等式①得:x≤1
解不等式②得:x>-2
∴不等式组的解集为:-2<x≤1
2、你能直接说出下列不等式组的解
集吗
1、不等式组的概念
2、不等组的解集:不等式组中所有不等式的解集的公共部分
3、确定不等式组解集的方法:
①利用数轴:
②利用法则:
同大取大, 同小取小,
大于小的,小于大的,中间找 大于大的,小于小的,找不了
直观形象
方便快捷
题目涉及的主要知识或方法
建构本章知识体系
一
元
一
次
不
等
式
不等式
一元一次不等式
一元一次不等式组
不等式定义
不等式性质
一元一次不等式应用
不等式解集及表示方法
一元一次不等式定义
一元一次不等式解法
一元一次不等式组的定义
一元一次不等式组的解法
特殊化
组成
一
元
一
次
方
程
二
元
一
次
方
程
(组)
类比
学习
感受二元一次方程与一元一次方程、一元一次不等式(组)之间的关系
1、已知
题目
感受彼此关系
①若x=1时,则y=________
②若-4≤y<1时,则x的取值
范围_____________
①、当二元一次方程中的一个未知数取值确定时,二元一次方程就转化成一元一次方程,从而求出另一个未知数值
解:由2x+y=6得y=6-2x
∵ -4≤y<1
∴-4≤6-2x<1
解这个不等式组得:
<x≤5
②、当二元一次方程中的一个未知数取值范围确定时,可利用一元一次不等式(组)确定另一个未知数的取值范围
4
典例剖析
求不等式 的非正整数解.
解不等式,得x>-4,
解:
所以非正整数解是:-3,-2,-1,0 .
解题思路指导:
求不等式(组)特殊解时,一般先求出不等式(组)的解集,然后在解集范围内找出特殊解,必要时可借助于数轴,形象直观
典例剖析
解:
解题思路指导:
先求出方程(组)的解,即用k的代数式表示x、y;然后再列出k的不等式(组),最后解关于k的不等式(组)
如果关于x、y的方程组
的解满足条件
,求k的取值范围。
①+②得:5x+5y=k+4
∵0<x+y<1
∴0< <1
解不等式组得:-4<k<1
整体思想
请你静心反思,通过对本章内容的复习,你有哪些新的收获?把你的新认识与周围的伙伴们一起分享吧!
反思与分享
1、知识储备:①如果ab>0,那么_________________
如果ab<0,那么_________________
②如果 >0,那么________________
如果 <0,那么_________________
拓展与延伸
知识运用:请你尝试求下列不等式解集
<0
>0
a>0
b>0
a<0
b<0
或
a>0
b<0
a<0
b>0
或
a>0
b>0
a<0
b<0
或
a>0
b<0
a<0
b>0
或
解题思路指导:
<0
解:
∵
<0
∴ (1)
3x+6>0
2x-2<0
3x+6<0
2x-2>0
或(2)
解不等式组(1)得:-2< x<1
不等式组(2)无解
∴原不等式的解集为-2<x<1
利用除法法则进行分类讨论,从而解决问题
拓展与延伸
>0
解:
拓展与延伸
∵
>0
∴ x(x-3) >0
∴ (1)
x>0
x-3>0
x<0
x-3<0
或(2)
解不等式组(1)得:x>3
解不等式组(2)得:x<0
∴原不等式的解集为x>3或x<0
解题思路指导:
对不等式左边多项式因式分解,再利用乘法法则,将一元二次不等式转化为一元一次不等式
28.(本题满分10分) 小明家需要用钢管做防盗窗,按设计要求,其中需要长为0.8m,2.5m且粗细相同的钢管分别为100根,32根,并要求这些用料不能是焊接而成的.现钢材市场的这种规格的钢管每根为6m.
(1)试问一根6米长的钢管有哪些裁剪方法呢 请填写下空(余料作废).
方法1:当只裁剪长为0.8米的用料时,最多可剪 ▲ 根;
方法2:当先剪下1根2.5米的用料时,余下部分最多能剪0.8米长的用料 ▲ 根:
方法3:当先剪下 2根2.5米的用料时,余下部分最多能剪0.8米长的用料 ▲ 根.
(2)联合用(1)中的方法2和方法3各裁剪多少根6米长的钢管,才能刚好得到所需要的相应数量的材料
(3)小明经过探究发现:如果联合(1)中的二种或三种裁剪方法,还有多种方案能刚好得到所需要的相应数量的材料,并且所需要6m长的钢管与(2)中根数相同,试帮小明说明理由,并写出一种与(2)不同的裁剪方案.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
