苏科版七下数学9.5.1提公因式法分解因式课件(共23张PPT)
文档属性
| 名称 | 苏科版七下数学9.5.1提公因式法分解因式课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 251.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 10:59:33 | ||
图片预览







文档简介
因式分解
—— 提公因式法
【问题1】请你运用前面所学的知识填写:(口答)
【问题2】请你将上述等式反过来写分别可写成:
(3) x2 -2x+1 =
(1) m(a+b+c)=
(2) (a+1)(a-1)=
(3) (x-1)2 =
ma+mb+mc
a2 -1
x2 -2x+1
(1)ma+mb+mc=
(2)a2 -1 =
整式乘法
m(a+b+c)
(a+1)(a-1)
( x-1 )2
像这样,把一个多项式写成几个整式的积的形式, 这叫做多项式因式分解
[问题3]请观察等号左边、右边有什么特点?
(1) ma+mb+mc= m(a+b+c )
(2) a2 -1 =(a+1)(a-1)
(3) x2 -2x+1=(x-1)2
因式分解
(也叫分解因式)。
多项式
整式的积
【问题 4】
下列各式由左边到右边的变形,哪些是因式分解?
(1)a2+ab=a(a+b) ( )
(2)x2+3x+1= x(x+3)+1( )
(3) (a-2)(a+2)= a2 -4 ( )
(4) a2 -4 =(a-2)(a+2) ( )
(5) ( )
是
不是
不是
是
不是
把一个多项式写成几个整式的积的形式,
这叫做多项式因式分解
(6)8a2b3c=2a2·2b3·2c
(不是)
多项式
【问题5】请观察这个多项式有什么特点?
ax+ay+az
各项都含有因式a
一个多项式各项都含有的因式,
称为这个多项式各项的公因式.
ax+ay+az
多项式ax+ay+az的公因式是:a
下列多项式的各项是否有公因式?
如果有,试找出公因式。
(1) m3n2+m2n5
(2) 2xy2z-6x2y3
(3) ab+bc-cd
m2n2
2xy2
没有
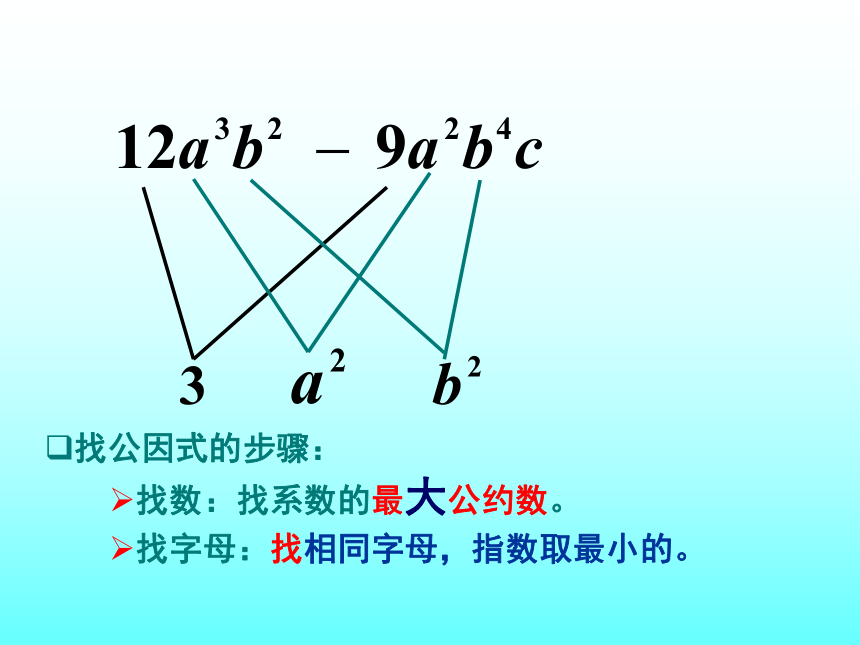
1.找数:
总结
【问题6】请你想一想,各项的公因式是如何找到的?
找系数的最大公约数。
2.找字母
:找相同字母,指数取最小的。
一个多项式各项都含有的因式,
称为这个多项式各项的公因式.
找数:找系数的最大公约数。
找字母:找相同字母,指数取最小的。
找公因式的步骤:
1.找数:找系数的最大公约数。
2.找字母:找相同字母,指数取最小的。
总结
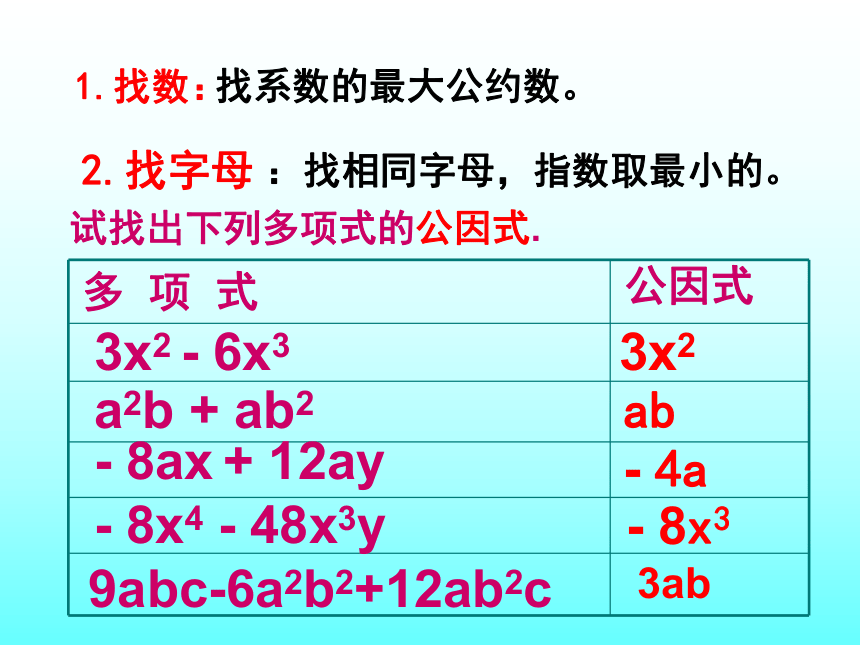
找公因式的步骤
多 项 式
公因式
- 8ax + 12ay
a2b + ab2
3x2 - 6x3
ab
- 4a
3x2
- 8x4 - 48x3y
- 8x3
试找出下列多项式的公因式.
9abc-6a2b2+12ab2c
3ab
1.找数:
找系数的最大公约数。
2.找字母
:找相同字母,指数取最小的。
9abc-6a2b2+12abc2各项的公因式是____.
3ab
因此有9abc- 6a2b2+12abc2
解原式=3ab·3c- 3ab·2ab+3ab·4c2
=3ab(3c- 2ab+4c2)
像这样,
把一个多项式写成几个整式的积的形式叫做把这个多项式因式分解。
1.找公因式
2.分离公因式
3.提取公因式
(也叫分解因式)。
分解因式
(1)12ab2c-6ab
1.找公因式
2.分离公因式
3.提取公因式
(2)-2m3+8m2-12m
注意:
多项式第一项是负号时,要提取出,提出后括号内各项要变号。
方法技巧:
为了检验结果是否正确,用整式乘法运算来检验。
若提全家走,留1把家守
例
分解因式:
注意:
多项式中的系数是分数时,把分数提取出来,使括号内各项的系数是整数。
1.找公因式
2.分离公因式
3.提取公因式
方法技巧:
为了检验结果是否正确,用整式乘法运算来检验。
例
把下列各式分解因式:
(1) 5y3 + 20y2
(2) - 24m2n + 16mn2 - 4m
一般地,如果多项式的各项含有公因式,可以把这个公因式提到括号外,将多项式写成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法。
综合练习
提公因式法
没提净
漏项,没留“1”
提负没变号
未成乘积形式
判断下列因式分解是否正确,若不正确,请说明理由。
火眼金睛
提公因式法要点:
1.提净公因式;
2.若提全家走,留1把家守;
3.提正不变号,提负要变号。
综合练习
1.分解因式:
解:原式= (x+y)(3a-2b)
公因式可以是一个单项式,也可以是一个多项式。
3a(x+y) – 2b(x+y)
变化练习
2.分解因式
(1)3a(x-y)-6(x-y) (2)2(a-1)+a(1-a)
变化练习
(3) 3m(x-y)2-9(y-x)3 (4)4a(a-b)3-12(b-a)3
公因式可以是一个单项式,也可以是一个多项式。
1.把下列各式分解因式:
(1) 7(a-b)4-14b(b-a)3 (2) (x + 2)2 - 4x - 8
拓展应用
注意
1.有同类项要合并;
2.结果首项负号要提出
2.解方程:
(5x-12)(9x+5)-(9x-7)(5x-12)=0
拓展应用
解: (5x-12)(9x+5-9x+7)=0
(5x-12).12=0
5x=12
1.试说明5101-599一定能被12整除.
能力提升
2.试说明
32013-4×32012+10×32011能被7整除
能力提升
课堂小结
请问这堂课你收获了什么?
提公因式法因式分解的步骤:
一找:找出公因式;
二分:分离公因式:
三提:提出公因式。
提公因式法分解因式应注意的问题:
(1)公因式要提尽;
(2)不能漏写“1”
(3)有同类项要合并,结果首项负号要提出
方法技巧:
为了检验结果是否正确,可以用整式乘法来检验。
总 结
如果多项式的各项有公因式,那么就可以把这个公因式提出来,把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法.
—— 提公因式法
【问题1】请你运用前面所学的知识填写:(口答)
【问题2】请你将上述等式反过来写分别可写成:
(3) x2 -2x+1 =
(1) m(a+b+c)=
(2) (a+1)(a-1)=
(3) (x-1)2 =
ma+mb+mc
a2 -1
x2 -2x+1
(1)ma+mb+mc=
(2)a2 -1 =
整式乘法
m(a+b+c)
(a+1)(a-1)
( x-1 )2
像这样,把一个多项式写成几个整式的积的形式, 这叫做多项式因式分解
[问题3]请观察等号左边、右边有什么特点?
(1) ma+mb+mc= m(a+b+c )
(2) a2 -1 =(a+1)(a-1)
(3) x2 -2x+1=(x-1)2
因式分解
(也叫分解因式)。
多项式
整式的积
【问题 4】
下列各式由左边到右边的变形,哪些是因式分解?
(1)a2+ab=a(a+b) ( )
(2)x2+3x+1= x(x+3)+1( )
(3) (a-2)(a+2)= a2 -4 ( )
(4) a2 -4 =(a-2)(a+2) ( )
(5) ( )
是
不是
不是
是
不是
把一个多项式写成几个整式的积的形式,
这叫做多项式因式分解
(6)8a2b3c=2a2·2b3·2c
(不是)
多项式
【问题5】请观察这个多项式有什么特点?
ax+ay+az
各项都含有因式a
一个多项式各项都含有的因式,
称为这个多项式各项的公因式.
ax+ay+az
多项式ax+ay+az的公因式是:a
下列多项式的各项是否有公因式?
如果有,试找出公因式。
(1) m3n2+m2n5
(2) 2xy2z-6x2y3
(3) ab+bc-cd
m2n2
2xy2
没有
1.找数:
总结
【问题6】请你想一想,各项的公因式是如何找到的?
找系数的最大公约数。
2.找字母
:找相同字母,指数取最小的。
一个多项式各项都含有的因式,
称为这个多项式各项的公因式.
找数:找系数的最大公约数。
找字母:找相同字母,指数取最小的。
找公因式的步骤:
1.找数:找系数的最大公约数。
2.找字母:找相同字母,指数取最小的。
总结
找公因式的步骤
多 项 式
公因式
- 8ax + 12ay
a2b + ab2
3x2 - 6x3
ab
- 4a
3x2
- 8x4 - 48x3y
- 8x3
试找出下列多项式的公因式.
9abc-6a2b2+12ab2c
3ab
1.找数:
找系数的最大公约数。
2.找字母
:找相同字母,指数取最小的。
9abc-6a2b2+12abc2各项的公因式是____.
3ab
因此有9abc- 6a2b2+12abc2
解原式=3ab·3c- 3ab·2ab+3ab·4c2
=3ab(3c- 2ab+4c2)
像这样,
把一个多项式写成几个整式的积的形式叫做把这个多项式因式分解。
1.找公因式
2.分离公因式
3.提取公因式
(也叫分解因式)。
分解因式
(1)12ab2c-6ab
1.找公因式
2.分离公因式
3.提取公因式
(2)-2m3+8m2-12m
注意:
多项式第一项是负号时,要提取出,提出后括号内各项要变号。
方法技巧:
为了检验结果是否正确,用整式乘法运算来检验。
若提全家走,留1把家守
例
分解因式:
注意:
多项式中的系数是分数时,把分数提取出来,使括号内各项的系数是整数。
1.找公因式
2.分离公因式
3.提取公因式
方法技巧:
为了检验结果是否正确,用整式乘法运算来检验。
例
把下列各式分解因式:
(1) 5y3 + 20y2
(2) - 24m2n + 16mn2 - 4m
一般地,如果多项式的各项含有公因式,可以把这个公因式提到括号外,将多项式写成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法。
综合练习
提公因式法
没提净
漏项,没留“1”
提负没变号
未成乘积形式
判断下列因式分解是否正确,若不正确,请说明理由。
火眼金睛
提公因式法要点:
1.提净公因式;
2.若提全家走,留1把家守;
3.提正不变号,提负要变号。
综合练习
1.分解因式:
解:原式= (x+y)(3a-2b)
公因式可以是一个单项式,也可以是一个多项式。
3a(x+y) – 2b(x+y)
变化练习
2.分解因式
(1)3a(x-y)-6(x-y) (2)2(a-1)+a(1-a)
变化练习
(3) 3m(x-y)2-9(y-x)3 (4)4a(a-b)3-12(b-a)3
公因式可以是一个单项式,也可以是一个多项式。
1.把下列各式分解因式:
(1) 7(a-b)4-14b(b-a)3 (2) (x + 2)2 - 4x - 8
拓展应用
注意
1.有同类项要合并;
2.结果首项负号要提出
2.解方程:
(5x-12)(9x+5)-(9x-7)(5x-12)=0
拓展应用
解: (5x-12)(9x+5-9x+7)=0
(5x-12).12=0
5x=12
1.试说明5101-599一定能被12整除.
能力提升
2.试说明
32013-4×32012+10×32011能被7整除
能力提升
课堂小结
请问这堂课你收获了什么?
提公因式法因式分解的步骤:
一找:找出公因式;
二分:分离公因式:
三提:提出公因式。
提公因式法分解因式应注意的问题:
(1)公因式要提尽;
(2)不能漏写“1”
(3)有同类项要合并,结果首项负号要提出
方法技巧:
为了检验结果是否正确,可以用整式乘法来检验。
总 结
如果多项式的各项有公因式,那么就可以把这个公因式提出来,把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
