苏科版数学八年级下册:9.3 平行四边形 课件(共19张PPT)
文档属性
| 名称 | 苏科版数学八年级下册:9.3 平行四边形 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 432.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 23:44:31 | ||
图片预览




文档简介
平行四边形
下面的图片中,有你熟悉的哪些图形?
A
D
C
B
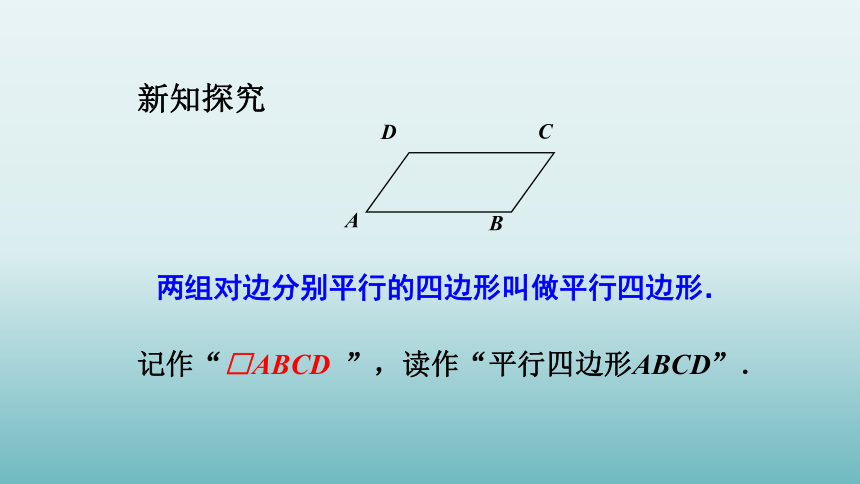
两组对边分别平行的四边形叫做平行四边形.
记作“□ABCD ”,读作“平行四边形ABCD”.
新知探究
操作思考
O是□ABCD对角线AC的中点.用透明纸覆盖在下图,描出□ABCD及其对角线AC,再用大头针钉在点O处,将透明纸上的□ABCD旋转1800.你有什么发现?
平行四边形是中心对称图形,对角线的交点是它的对称中心.
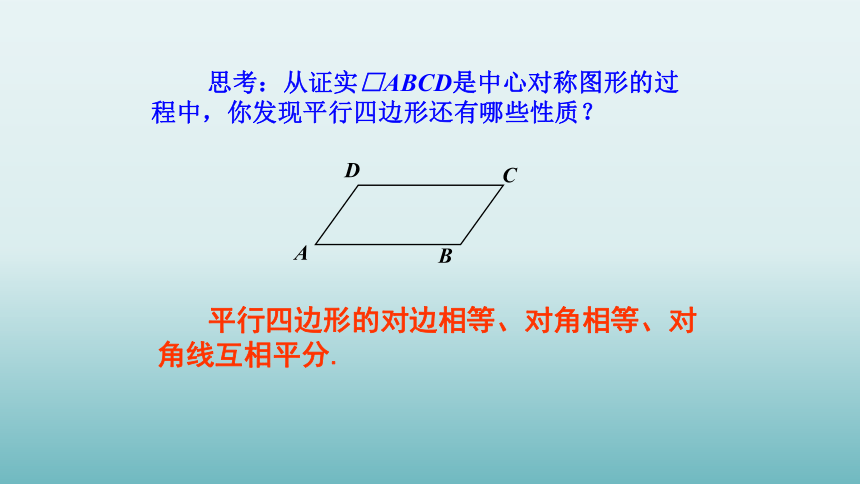
思考:从证实□ABCD是中心对称图形的过程中,你发现平行四边形还有哪些性质?
平行四边形的对边相等、对角相等、对角线互相平分.
A
D
C
B
归纳:平行四边形的性质
●平行四边形是中心对称图形.
●平行四边形的对边平行且相等.
●平行四边形的对角相等.
●平行四边形的对角线互相平分.
做一做
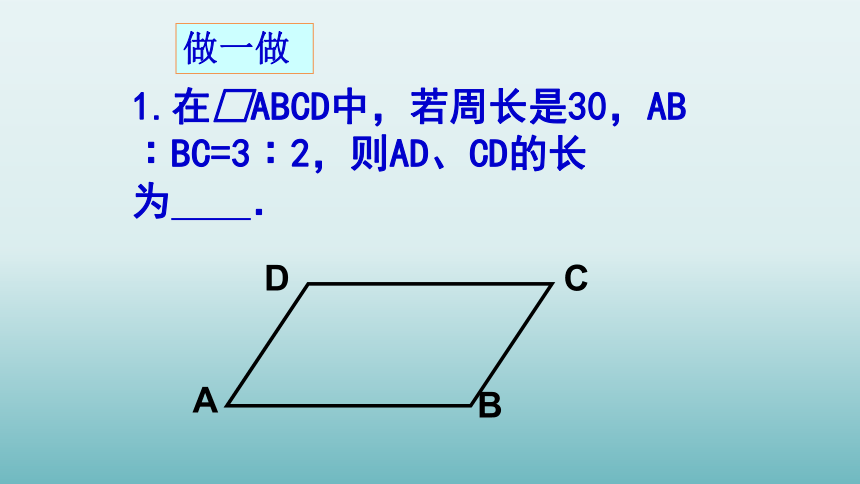
1.在□ABCD中,若周长是30,AB︰BC=3︰2,则AD、CD的长为 .
A
B
C
D
2.已知□ABCD中,∠A +∠C =120°,则∠A= ,∠D= .
做一做
A
B
C
D
3.如图,在□ABCD中,∠DAB的角平线交边CD于点E,AD=3,EC=2,则□ABCD的周长为= .
做一做
4.如图,△ABC中,AB=AC=16. D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.则四边形AEDF的周长为 .
A
B
C
D
E
F
新知应用
已知:如图,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD.求证:A、B、C分别是△EFD各边的中点.
A
B
C
D
E
F
思考:△ABC和△EFD的内角分别相等吗?为什么?你还能得到哪些结论?证明你的结论.
如图,在□ABCD中,∠B=50°,求这个四边形的其他内角的度数,并说明理由.
B
A
D
C
拓展延伸
如图:□ABCD的周长是36,由钝角顶点D向AB、BC引两条高DE、DF,且DE=4,DF=6,求这个平行四边形的面积.
E
C
B
F
A
D
1.已知,如图:□ABCD的对角线AC、BD相交于点O,直线EF过点O与AD、BC相交于点E、F,请说明:OE=OF.
E
O
B
A
F
D
C
若直线EF与CD、AB的延长线相交于E、F,上述结论还成立吗?如成立,请说明理由.
课堂训练
E
O
B
A
F
D
C
若直线EF与CD、AB的延长线相交于E、F,上述结论还成立吗?如成立,请说明理由.
2. 如图,M为□ABCD的一边AD上点,若△ADM的面积为S3,△MBC的面积为S2,△MDC的面积为S1,则S1 、S2 、S3之间的关系为 .
S1 =S2+S3
谢 谢!
2.一个平行四边形的一边长是10cm,一条对角线长是8cm,则它的另一条对角线长的取值范围是 .
12cm< x<28cm
3.如图,□ABCD的对角线相交于点O,AD≠DC,过点O作OM⊥AC,△CDM的周长
为a,则□ABCD的周长为 .
D
C
B
A
M
O
2a
5. 如图,在□ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,BE=2cm,DF=3cm, ∠1=60°, 求各角的度数与各边的长.
提示:直角三角形中30度的锐角所对的直角边等于斜边的一半(以后可直接用)
B
A
C
E
D
F
下面的图片中,有你熟悉的哪些图形?
A
D
C
B
两组对边分别平行的四边形叫做平行四边形.
记作“□ABCD ”,读作“平行四边形ABCD”.
新知探究
操作思考
O是□ABCD对角线AC的中点.用透明纸覆盖在下图,描出□ABCD及其对角线AC,再用大头针钉在点O处,将透明纸上的□ABCD旋转1800.你有什么发现?
平行四边形是中心对称图形,对角线的交点是它的对称中心.
思考:从证实□ABCD是中心对称图形的过程中,你发现平行四边形还有哪些性质?
平行四边形的对边相等、对角相等、对角线互相平分.
A
D
C
B
归纳:平行四边形的性质
●平行四边形是中心对称图形.
●平行四边形的对边平行且相等.
●平行四边形的对角相等.
●平行四边形的对角线互相平分.
做一做
1.在□ABCD中,若周长是30,AB︰BC=3︰2,则AD、CD的长为 .
A
B
C
D
2.已知□ABCD中,∠A +∠C =120°,则∠A= ,∠D= .
做一做
A
B
C
D
3.如图,在□ABCD中,∠DAB的角平线交边CD于点E,AD=3,EC=2,则□ABCD的周长为= .
做一做
4.如图,△ABC中,AB=AC=16. D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.则四边形AEDF的周长为 .
A
B
C
D
E
F
新知应用
已知:如图,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD.求证:A、B、C分别是△EFD各边的中点.
A
B
C
D
E
F
思考:△ABC和△EFD的内角分别相等吗?为什么?你还能得到哪些结论?证明你的结论.
如图,在□ABCD中,∠B=50°,求这个四边形的其他内角的度数,并说明理由.
B
A
D
C
拓展延伸
如图:□ABCD的周长是36,由钝角顶点D向AB、BC引两条高DE、DF,且DE=4,DF=6,求这个平行四边形的面积.
E
C
B
F
A
D
1.已知,如图:□ABCD的对角线AC、BD相交于点O,直线EF过点O与AD、BC相交于点E、F,请说明:OE=OF.
E
O
B
A
F
D
C
若直线EF与CD、AB的延长线相交于E、F,上述结论还成立吗?如成立,请说明理由.
课堂训练
E
O
B
A
F
D
C
若直线EF与CD、AB的延长线相交于E、F,上述结论还成立吗?如成立,请说明理由.
2. 如图,M为□ABCD的一边AD上点,若△ADM的面积为S3,△MBC的面积为S2,△MDC的面积为S1,则S1 、S2 、S3之间的关系为 .
S1 =S2+S3
谢 谢!
2.一个平行四边形的一边长是10cm,一条对角线长是8cm,则它的另一条对角线长的取值范围是 .
12cm< x<28cm
3.如图,□ABCD的对角线相交于点O,AD≠DC,过点O作OM⊥AC,△CDM的周长
为a,则□ABCD的周长为 .
D
C
B
A
M
O
2a
5. 如图,在□ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,BE=2cm,DF=3cm, ∠1=60°, 求各角的度数与各边的长.
提示:直角三角形中30度的锐角所对的直角边等于斜边的一半(以后可直接用)
B
A
C
E
D
F
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
