苏科版数学八年级下册《10 分式》小结与思考1-2 课件 (共29张PPT)
文档属性
| 名称 | 苏科版数学八年级下册《10 分式》小结与思考1-2 课件 (共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 23:48:34 | ||
图片预览







文档简介
第十章 小结与思考(1)
1、在代数式
分式有________个
分式:形如 的式子,A、B为整式,
且B中含有字母
(1)分式的定义.
一. 分式的基本概念
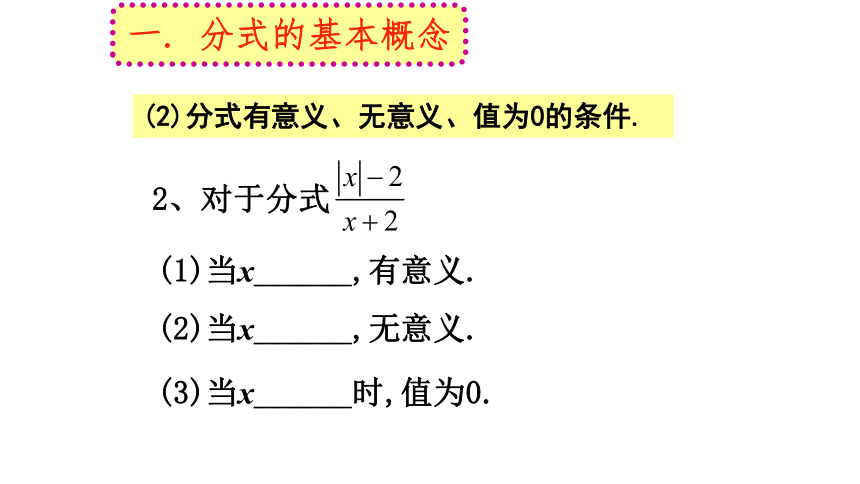
2、对于分式
(1)当x______,有意义.
(2)当x______,无意义.
(3)当x______时,值为0.
(2)分式有意义、无意义、值为0的条件.
一. 分式的基本概念
3、如果把分式 中的x、y都扩大为原来的2倍,那么该分式的值( )
A、扩大为原来的2倍
B、缩小为原来的一半
C、不变
D、缩小为原来的四分之一
二. 分式的基本性质
4、下列分式中,最简分式是 ( )
二. 分式的基本性质
5、
的最简公分母是_______
的最简公分母是_______
二. 分式的基本性质
6、计算:
三. 分式的运算
三. 分式的运算
7、
8、已知 ,求
概念
基本性质
约分
通分
分式的加减法则
分式的乘除法则
分式的乘方法则
混合运算顺序
方程
概念
解分式方程的一般步骤
增根
解应用题
分式
分式有意义
分式的值为0
的形式
B中含有字母B≠0
分式无意义
第十章 小结与思考(2)
概念
基本性质
约分
通分
分式的加减法则
分式的乘除法则
分式的乘方法则
混合运算顺序
方程
概念
解分式方程的一般步骤
增根
解应用题
分式
分式有意义
分式的值为0
的形式
B中含有字母B≠0
分式无意义
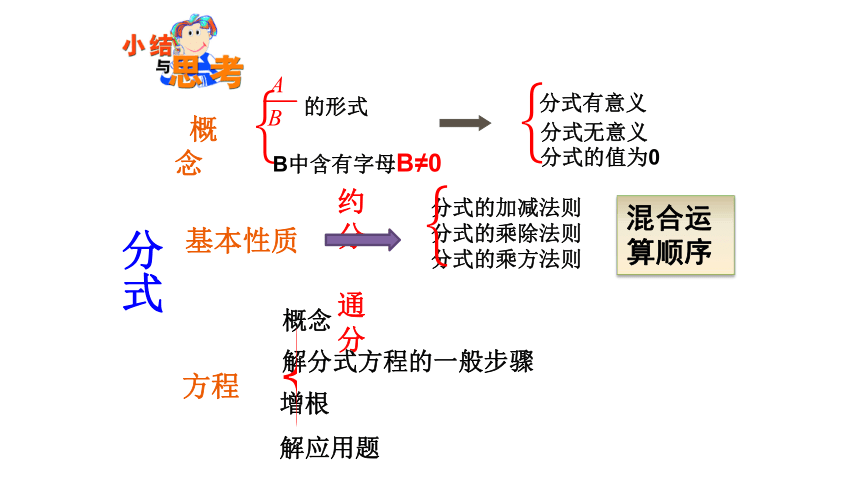
知识结构
分母中含有未知数的方程叫做分式方程。
一、分式方程--定义
1、下列方程中是分式方程的是 .
(2)(3)(6)
1、解下列方程:
二、分式方程--解方程
1、解下列方程:
二、分式方程--解方程
解:方程两边同乘以 ,得
检验:当x=-1时,2x-1=-3≠0,
∴x=-1是原方程的解.
解之,得
1、解下列方程:
二、分式方程--解方程
解:方程两边同乘以 ,得
检验:当x=3时,(x+3)(x-3)=0,
∴x=3是增根,
∴原方程无解.
解之,得
一般步骤:
1、化:方程两边同乘以各分母的最简公分母,
将分式方程转化为整式方程;
2、解:解这个整式方程;
3、检:检验是否是原方程的解(检验最简公分母是否为0);
4、答:写出原方程的根;
二、分式方程--解方程
1、若方程 有增根,则增根是_______ ,
a的值是________.
三、分式方程--增根问题
使得最简公分母为0的解叫方程的增根,此时原分式方程无解。
解方程,方程两边同乘以(x-3),得
方程有增根为 x=3,代入得
综上,a=1.
分析:
x=3
1
方程的最简公分母是 (x-3)
∴要使最简公分母为0,有
x-3=0
∴方程的增根是 x=3
2、(1)关于x的分式方程 的解为正数,
则m的取值范围为 .
(2)解关于x的分式方程 时会产生增根,则增根可能为 .
三、分式方程--增根问题
(1)关于x的分式方程 的解为正数,则m的取值范围为 .
解为正数,说明:方程有解,解不是增根;且解为正数
解方程,方程两边同乘以(x-1),得
∵方程的解为正数
∴方程有解,解不是增根,且为正数
m>2且m≠3
分析:
∴
∴m>2且m≠3.
三、分式方程--增根问题
(2)解关于x的分式方程 时会产生增根,则增根可能为 .
使得最简公分母为0的解叫方程的增根。
方程的最简公分母是 x(x-3)
∴要使最简公分母 x(x-3)=0,有
x=0 或 x-3=0
∴方程的增根是 x=0 或 x=3
x=0 或 x=3
分析:
三、分式方程--增根问题
(直接设,间接设)
列分式方程解应用题步骤为:
1审
(审题)
3设
4列
(根据等量关系列出方程)
5解(解这个方程)
7答(完整地写出答案,注意单位)
6验
(既要验是否为所列分式方程的根,
又要验是否符合实际情况)
2找
(找出等量关系)
四、分式方程--应用
1、某工程在招标时,接到甲、乙两个工程队的投标书,施工一天需付甲工程队工程款1.5万元,需付乙工程队工程款1.1万元.工程领导小组根据甲、乙两队的投标书测算,可有以下三种施工方案:
A.甲队单独完成这项工程刚好如期完成;
B.乙队单独完成这项工程比规定日期多用5天;
C.若甲、乙两队合作4天,余下的工程由乙队单独做也正好如期完成.
在不耽误工程的前提下,你觉得哪一种施工方案最节省工程款?
注:把“工作总量”看做单位“1”
四、分式方程--应用
分析:相等关系:甲乙合作4天的工作总量+乙单独完成的工作总量=1
解:设规定的工期为 x 天,则乙完成需要(x+5)天.
由题意,得
解之,得
经检验:x=20是原方程的解,且符合题意.
答:在不耽误工程的前提下,C种施工方案最节省工程款.
这三种施工方案需要的工程款为:
A:1.5×20=30(万元)
B:1.1×(20+5)=27.5(万元)
C:(1.5+1.1)×4+1.1×(20-4)=28(万元)
综上,在保证正常完工的前提下,由28<30,知应选择C种方案.
工作总量=工作效率×工作时间
四、分式方程--应用
练习、某中学组织学生到离学校15km的东山游玩,先遣队与大队同时出发,先遣队的速度是大队的1.2倍,结果先遣队比大队早到0.5h,先遣队和大队的速度各是多少?
分析:相等关系:大队时间-先遣队时间=0.5h
解:设大队的速度是 x km/h,则先遣队的速度是 1.2x km/h.
由题意,得
解之,得
经检验:x=5是原方程的解,且符合题意.
∴ 1.2x=1.2×5=6.
答:大队的速度是 5 km/h,先遣队的速度是 6 km/h.
时间=路程÷速度
四、分式方程--应用
2、某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
四、分式方程--应用
(1)分析:相等关系:第一批衬衫的进价-第二批衬衫的进价=10元
解:设第二次购进衬衫 x 件,则第一次购进衬衫 2x 件.
由题意,得
解之,得
经检验:x=15是原方程的解,且符合题意.
答:第一次购进衬衫30件,则第二次购进衬衫15件.
∴2x=30
2、某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
单价=总价÷数量
四、分式方程--应用
(2)由(1)可求得:
第一次购进衬衫的单价为4500÷30=150元/件,
第二次购进衬衫的单价为2100÷15=140元/件.
设第二批衬衫的售价为 y元/件,由题意,得
解之,得
答:第二批衬衫每件至少要售170元.
2、某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
利润=售价-进价
四、分式方程--应用
1、在代数式
分式有________个
分式:形如 的式子,A、B为整式,
且B中含有字母
(1)分式的定义.
一. 分式的基本概念
2、对于分式
(1)当x______,有意义.
(2)当x______,无意义.
(3)当x______时,值为0.
(2)分式有意义、无意义、值为0的条件.
一. 分式的基本概念
3、如果把分式 中的x、y都扩大为原来的2倍,那么该分式的值( )
A、扩大为原来的2倍
B、缩小为原来的一半
C、不变
D、缩小为原来的四分之一
二. 分式的基本性质
4、下列分式中,最简分式是 ( )
二. 分式的基本性质
5、
的最简公分母是_______
的最简公分母是_______
二. 分式的基本性质
6、计算:
三. 分式的运算
三. 分式的运算
7、
8、已知 ,求
概念
基本性质
约分
通分
分式的加减法则
分式的乘除法则
分式的乘方法则
混合运算顺序
方程
概念
解分式方程的一般步骤
增根
解应用题
分式
分式有意义
分式的值为0
的形式
B中含有字母B≠0
分式无意义
第十章 小结与思考(2)
概念
基本性质
约分
通分
分式的加减法则
分式的乘除法则
分式的乘方法则
混合运算顺序
方程
概念
解分式方程的一般步骤
增根
解应用题
分式
分式有意义
分式的值为0
的形式
B中含有字母B≠0
分式无意义
知识结构
分母中含有未知数的方程叫做分式方程。
一、分式方程--定义
1、下列方程中是分式方程的是 .
(2)(3)(6)
1、解下列方程:
二、分式方程--解方程
1、解下列方程:
二、分式方程--解方程
解:方程两边同乘以 ,得
检验:当x=-1时,2x-1=-3≠0,
∴x=-1是原方程的解.
解之,得
1、解下列方程:
二、分式方程--解方程
解:方程两边同乘以 ,得
检验:当x=3时,(x+3)(x-3)=0,
∴x=3是增根,
∴原方程无解.
解之,得
一般步骤:
1、化:方程两边同乘以各分母的最简公分母,
将分式方程转化为整式方程;
2、解:解这个整式方程;
3、检:检验是否是原方程的解(检验最简公分母是否为0);
4、答:写出原方程的根;
二、分式方程--解方程
1、若方程 有增根,则增根是_______ ,
a的值是________.
三、分式方程--增根问题
使得最简公分母为0的解叫方程的增根,此时原分式方程无解。
解方程,方程两边同乘以(x-3),得
方程有增根为 x=3,代入得
综上,a=1.
分析:
x=3
1
方程的最简公分母是 (x-3)
∴要使最简公分母为0,有
x-3=0
∴方程的增根是 x=3
2、(1)关于x的分式方程 的解为正数,
则m的取值范围为 .
(2)解关于x的分式方程 时会产生增根,则增根可能为 .
三、分式方程--增根问题
(1)关于x的分式方程 的解为正数,则m的取值范围为 .
解为正数,说明:方程有解,解不是增根;且解为正数
解方程,方程两边同乘以(x-1),得
∵方程的解为正数
∴方程有解,解不是增根,且为正数
m>2且m≠3
分析:
∴
∴m>2且m≠3.
三、分式方程--增根问题
(2)解关于x的分式方程 时会产生增根,则增根可能为 .
使得最简公分母为0的解叫方程的增根。
方程的最简公分母是 x(x-3)
∴要使最简公分母 x(x-3)=0,有
x=0 或 x-3=0
∴方程的增根是 x=0 或 x=3
x=0 或 x=3
分析:
三、分式方程--增根问题
(直接设,间接设)
列分式方程解应用题步骤为:
1审
(审题)
3设
4列
(根据等量关系列出方程)
5解(解这个方程)
7答(完整地写出答案,注意单位)
6验
(既要验是否为所列分式方程的根,
又要验是否符合实际情况)
2找
(找出等量关系)
四、分式方程--应用
1、某工程在招标时,接到甲、乙两个工程队的投标书,施工一天需付甲工程队工程款1.5万元,需付乙工程队工程款1.1万元.工程领导小组根据甲、乙两队的投标书测算,可有以下三种施工方案:
A.甲队单独完成这项工程刚好如期完成;
B.乙队单独完成这项工程比规定日期多用5天;
C.若甲、乙两队合作4天,余下的工程由乙队单独做也正好如期完成.
在不耽误工程的前提下,你觉得哪一种施工方案最节省工程款?
注:把“工作总量”看做单位“1”
四、分式方程--应用
分析:相等关系:甲乙合作4天的工作总量+乙单独完成的工作总量=1
解:设规定的工期为 x 天,则乙完成需要(x+5)天.
由题意,得
解之,得
经检验:x=20是原方程的解,且符合题意.
答:在不耽误工程的前提下,C种施工方案最节省工程款.
这三种施工方案需要的工程款为:
A:1.5×20=30(万元)
B:1.1×(20+5)=27.5(万元)
C:(1.5+1.1)×4+1.1×(20-4)=28(万元)
综上,在保证正常完工的前提下,由28<30,知应选择C种方案.
工作总量=工作效率×工作时间
四、分式方程--应用
练习、某中学组织学生到离学校15km的东山游玩,先遣队与大队同时出发,先遣队的速度是大队的1.2倍,结果先遣队比大队早到0.5h,先遣队和大队的速度各是多少?
分析:相等关系:大队时间-先遣队时间=0.5h
解:设大队的速度是 x km/h,则先遣队的速度是 1.2x km/h.
由题意,得
解之,得
经检验:x=5是原方程的解,且符合题意.
∴ 1.2x=1.2×5=6.
答:大队的速度是 5 km/h,先遣队的速度是 6 km/h.
时间=路程÷速度
四、分式方程--应用
2、某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
四、分式方程--应用
(1)分析:相等关系:第一批衬衫的进价-第二批衬衫的进价=10元
解:设第二次购进衬衫 x 件,则第一次购进衬衫 2x 件.
由题意,得
解之,得
经检验:x=15是原方程的解,且符合题意.
答:第一次购进衬衫30件,则第二次购进衬衫15件.
∴2x=30
2、某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
单价=总价÷数量
四、分式方程--应用
(2)由(1)可求得:
第一次购进衬衫的单价为4500÷30=150元/件,
第二次购进衬衫的单价为2100÷15=140元/件.
设第二批衬衫的售价为 y元/件,由题意,得
解之,得
答:第二批衬衫每件至少要售170元.
2、某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
利润=售价-进价
四、分式方程--应用
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
