苏科版数学八年级下册《12 二次根式》小结与思考 课件 (共22张PPT)
文档属性
| 名称 | 苏科版数学八年级下册《12 二次根式》小结与思考 课件 (共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 426.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 23:51:21 | ||
图片预览



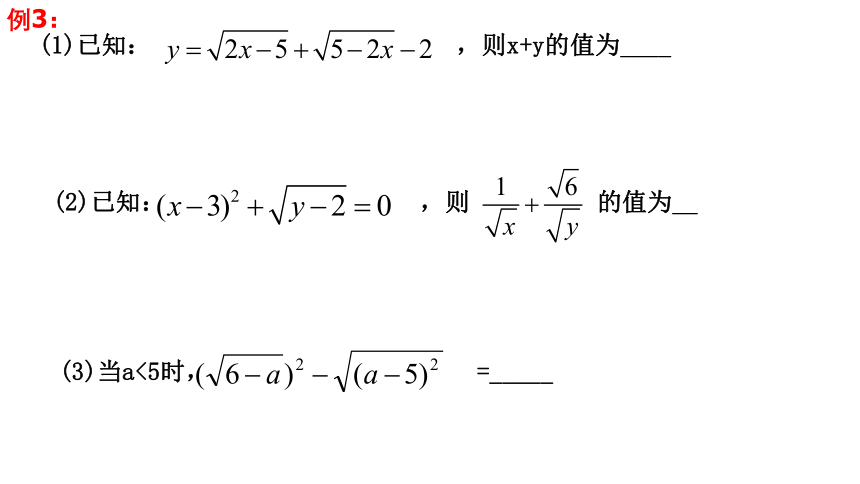


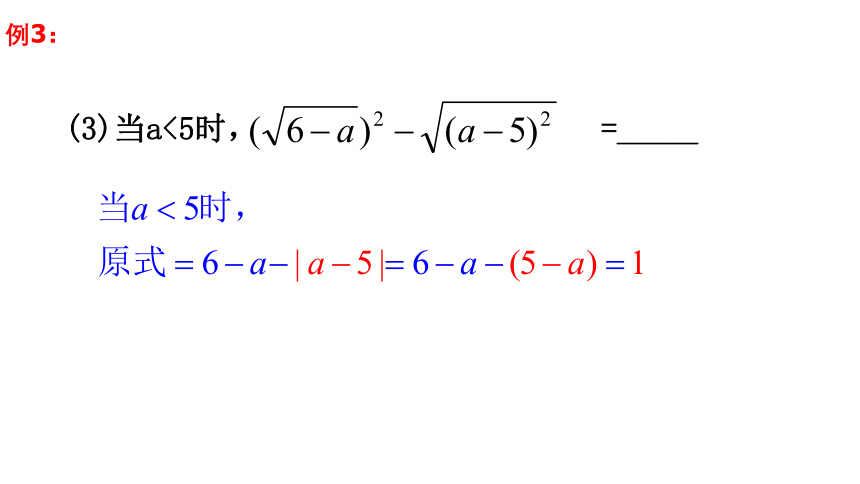


文档简介
第12章《二次根式》小结与思考
例1(1)下列式子是二次根式的有________
⑤
④
①
②
③
【知识点1】二次根式的概念
一般地,形如 的式子叫二次根式
①③
例1(2)写出使下列各式成立的字母的取值范围
【知识点2】二次根式的性质
a
非负
|a|
例2(1)填空
(2)计算
5
7
(1)已知: ,则x+y的值为____
(2)已知: ,则 的值为__
(3)当a<5时, =_____
例3:
(1)已知: ,
则x+y的值为____
由题意得2x-5 ≥0且5-2x ≥0
∴ x=2.5
此时y=-2
x+y=2.5-2=0.5
例3:
(2)已知: ,
则 的值为 __
由题意得x-3=0且y-2 =0
∴ x=3,y=2
例3:
(3)当a<5时, =_____
例3:
例4:下列等式中,字母分别符合什么条件?
①
②
③
例5:在实数范围内分解因式:
(1)
(2)
【知识点3】二次根式的运算
3. 二次根式相加减,实际上是先_________二次根式,
再合并 二次根式.
化简
同类
例6:
4
经过化简后,被开方数相同的
二次根式称为同类二次根式.
【知识点4】同类二次根式
【知识点5】最简二次根式
(1)被开方数中不含能开得尽方的因数或因式;
(2)被开方数中不含分母;
(3)分母中不含有根号.
例7:计算
(3)
(3)
1.
2.m是 的小数部分,则
的值为____
【能力提升】二次根式的应用
例8:
1.
2.m是 的小数部分,则
的值为____
由题意得m=
例9(2)如图长方形内两相邻正方形的面积分别是8和3,则长方形内阴影部分的面积是_______
例9(3)在矩形ABCD中,AB=a, BC=b, M是BC的中点,DE⊥AM,垂足为E,用含a,b的代数式表示DE的长.
∵矩形ABCD
∴ ∠B=90°,BC=AD=b
∵M是BC的中点
∴BM=
∵∠B=90°
∴
∴
A
B
C
D
E
图②
M
二 次 根 式
三个概念
四种运算
二次根式
最简二次根式
加 、减、乘、除
课堂小结
同类二次根式
三个性质
三个性质
谢谢!
例1(1)下列式子是二次根式的有________
⑤
④
①
②
③
【知识点1】二次根式的概念
一般地,形如 的式子叫二次根式
①③
例1(2)写出使下列各式成立的字母的取值范围
【知识点2】二次根式的性质
a
非负
|a|
例2(1)填空
(2)计算
5
7
(1)已知: ,则x+y的值为____
(2)已知: ,则 的值为__
(3)当a<5时, =_____
例3:
(1)已知: ,
则x+y的值为____
由题意得2x-5 ≥0且5-2x ≥0
∴ x=2.5
此时y=-2
x+y=2.5-2=0.5
例3:
(2)已知: ,
则 的值为 __
由题意得x-3=0且y-2 =0
∴ x=3,y=2
例3:
(3)当a<5时, =_____
例3:
例4:下列等式中,字母分别符合什么条件?
①
②
③
例5:在实数范围内分解因式:
(1)
(2)
【知识点3】二次根式的运算
3. 二次根式相加减,实际上是先_________二次根式,
再合并 二次根式.
化简
同类
例6:
4
经过化简后,被开方数相同的
二次根式称为同类二次根式.
【知识点4】同类二次根式
【知识点5】最简二次根式
(1)被开方数中不含能开得尽方的因数或因式;
(2)被开方数中不含分母;
(3)分母中不含有根号.
例7:计算
(3)
(3)
1.
2.m是 的小数部分,则
的值为____
【能力提升】二次根式的应用
例8:
1.
2.m是 的小数部分,则
的值为____
由题意得m=
例9(2)如图长方形内两相邻正方形的面积分别是8和3,则长方形内阴影部分的面积是_______
例9(3)在矩形ABCD中,AB=a, BC=b, M是BC的中点,DE⊥AM,垂足为E,用含a,b的代数式表示DE的长.
∵矩形ABCD
∴ ∠B=90°,BC=AD=b
∵M是BC的中点
∴BM=
∵∠B=90°
∴
∴
A
B
C
D
E
图②
M
二 次 根 式
三个概念
四种运算
二次根式
最简二次根式
加 、减、乘、除
课堂小结
同类二次根式
三个性质
三个性质
谢谢!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
