苏科版数学七年级下册 7.5 多边形的内角和与外角和 第1课时 课件 (共36张PPT)
文档属性
| 名称 | 苏科版数学七年级下册 7.5 多边形的内角和与外角和 第1课时 课件 (共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览





文档简介
三角形蓝和三角形红见面了,蓝炫耀的说:“我的面积比你大,所以我的内角和也比你大!”红不服气的说:“那可不好说噢,你自己量量看!”
蓝用量角器量了量自己的内角和,就不再说话了!
你知道为什么吗?
情境问题
三角形的内角和是180度.
7.5 多边形的内角和(1)
探索三角形内角和定理
你有什么方法可以验证呢?
任意画一个三角形,量一量
探索三角形内角和定理
7.5 多边形的内角和(1)
锐角三角形
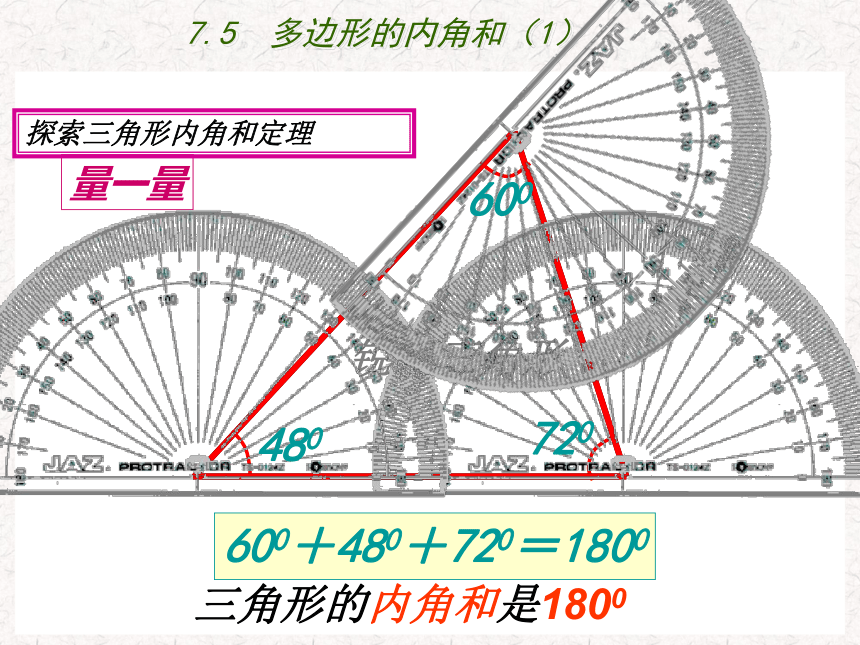
量一量
480
720
600
600+480+720=1800
探索三角形内角和定理
三角形的内角和是1800
7.5 多边形的内角和(1)
3
2
3
1
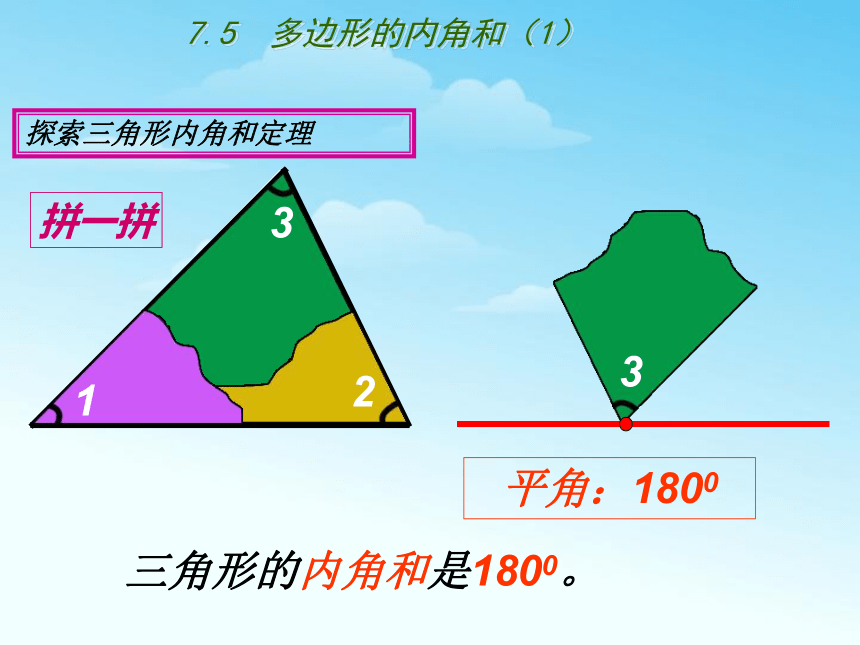
平角:1800
三角形的内角和是1800。
拼一拼
探索三角形内角和定理
7.5 多边形的内角和(1)
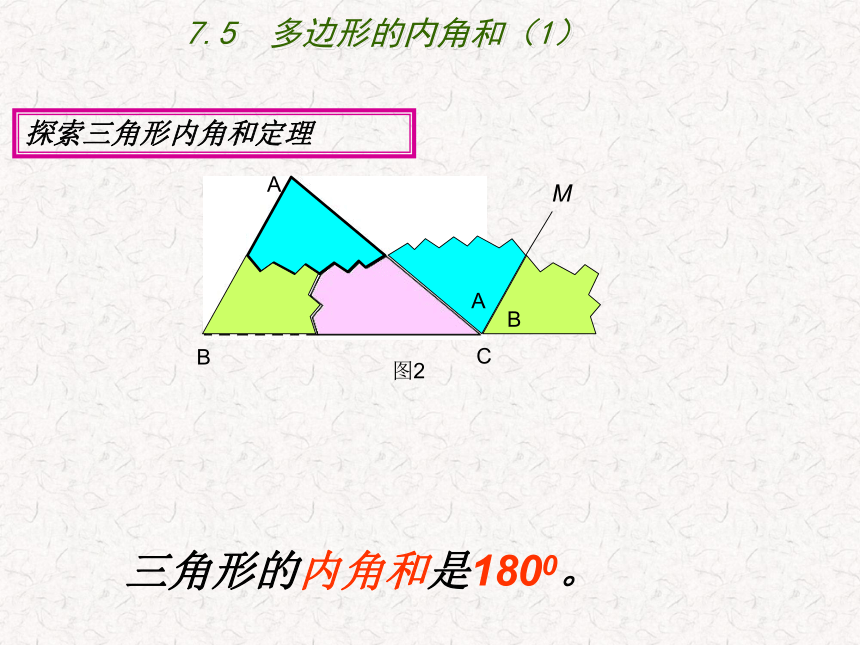
图2
A
B
C
A
B
M
探索三角形内角和定理
三角形的内角和是1800。
7.5 多边形的内角和(1)
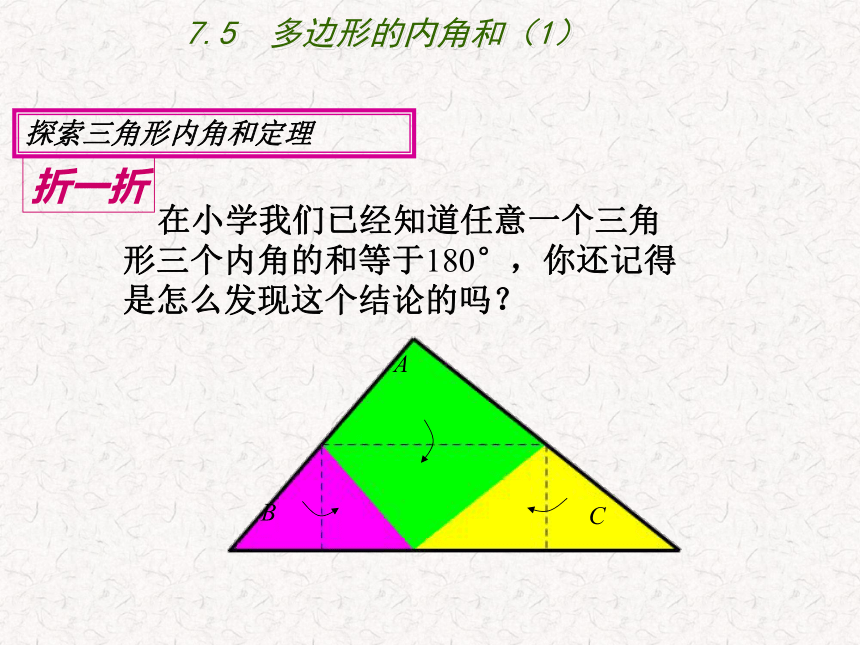
在小学我们已经知道任意一个三角形三个内角的和等于180°,你还记得是怎么发现这个结论的吗?
A
B
C
折一折
探索三角形内角和定理
7.5 多边形的内角和(1)
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
折一折
探索三角形内角和定理
三角形的内角和是1800。
7.5 多边形的内角和(1)
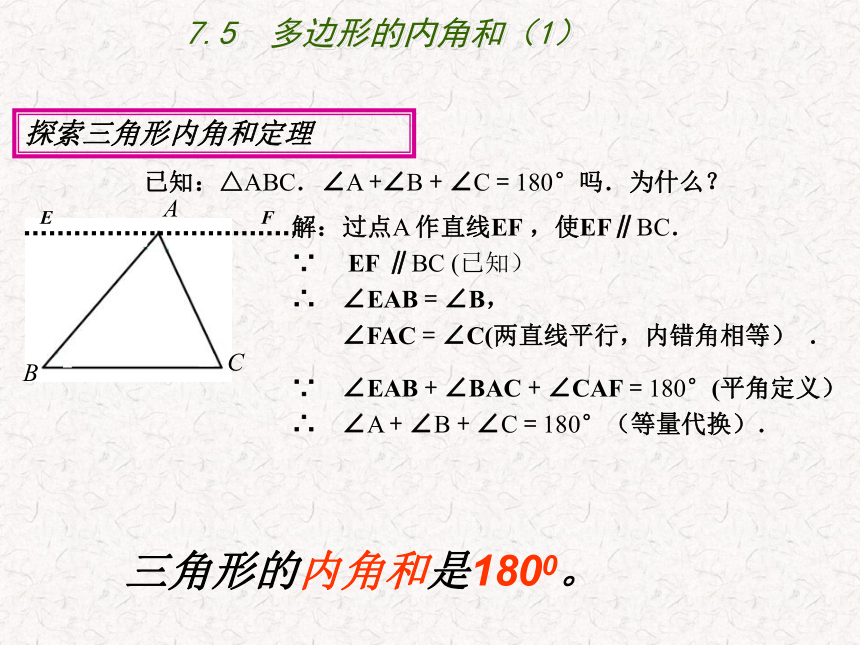
解:过点A 作直线EF ,使EF∥BC.
∵ EF ∥BC (已知)
∴ ∠EAB = ∠B,
∠FAC = ∠C(两直线平行,内错角相等) .
已知:△ABC.∠A +∠B + ∠C = 180°吗.为什么?
A
B
C
E
F
∵ ∠EAB + ∠BAC + ∠CAF = 180°(平角定义)
∴ ∠A + ∠B + ∠C = 180°(等量代换).
三角形的内角和是1800。
探索三角形内角和定理
7.5 多边形的内角和(1)
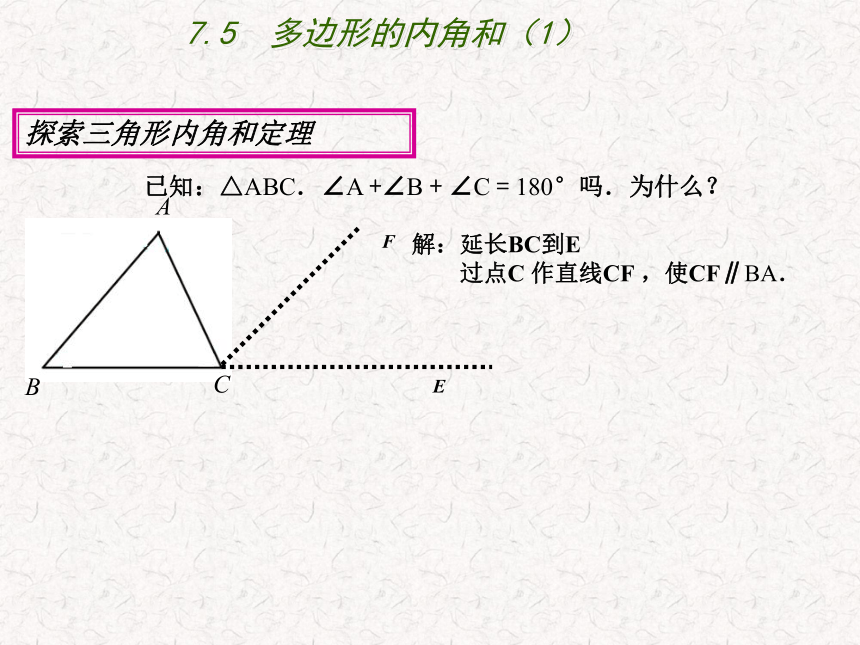
已知:△ABC.∠A +∠B + ∠C = 180°吗.为什么?
A
B
C
E
F
探索三角形内角和定理
7.5 多边形的内角和(1)
解:延长BC到E
过点C 作直线CF ,使CF∥BA.
追问1 通过前面的验证过程,你能受到什么启发?你能用其他方法验证此定理吗?
C
A
B
1
2
3
4
5
l
探索三角形内角和定理
7.5 多边形的内角和(1)
解:延长BC到E
过点C 作直线CF ,使CF∥BA.
C
A
B
1
2
3
4
5
l
P
6
m
探索三角形内角和定理
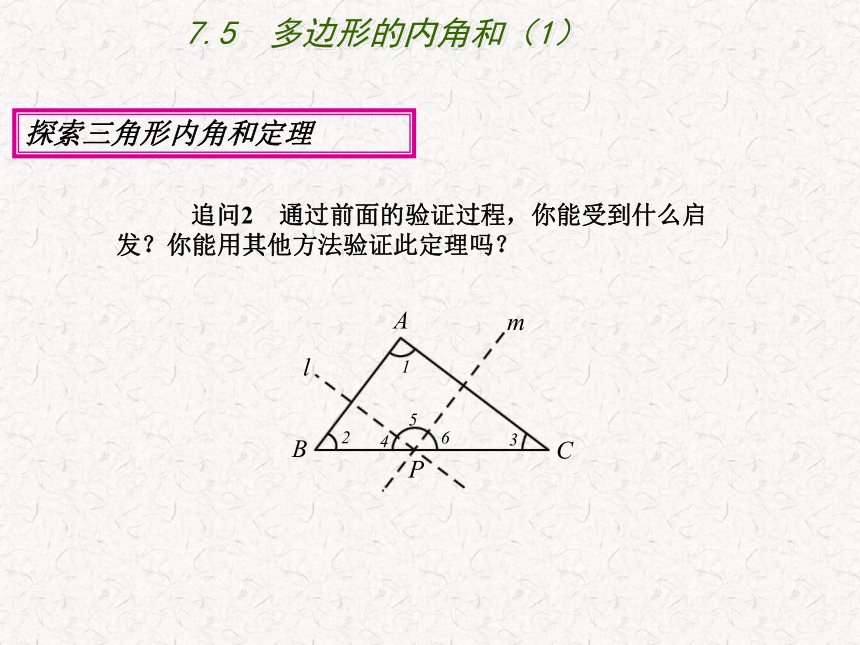
追问2 通过前面的验证过程,你能受到什么启发?你能用其他方法验证此定理吗?
7.5 多边形的内角和(1)
C
A
B
1
2
3
4
5
l
P
6
m
n
探索三角形内角和定理
追问3 通过前面的验证过程,你能受到什么启发?你能用其他方法验证此定理吗?
7.5 多边形的内角和(1)
C
A
B
1
2
3
4
5
l
P
6
m
n
探索三角形内角和定理
追问4 通过前面的验证过程,你能受到什么启发?你能用其他方法验证此定理吗?
7.5 多边形的内角和(1)
为了说明的需要,在原来的图形上添画的线叫做辅助线。
方法小结
为了说明三个角的和为1800,转化为一个平角,这种转化思想是数学中的常用思想方法.
思路小结
探索三角形内角和定理
三角形的内角和是1800。
7.5 多边形的内角和(1)
在一个三角形的3个内角中,最多能有几个直角?最多能有几个钝角呢?为什么?
想一想
7.5 多边形的内角和(1)
三角形的内角和是1800。
1.根据下图填空:
(1)n= ; (2)x= ; (3)y= .
81°
72°
n°
(1)
x°
x°
(2)
∟
31°
y°
(3)
122°
27°
29°
59°
2.在直角△ABC中,∠C=90°,∠A+∠B= .
90°
7.5 多边形的内角和(1)
巩固练习
直角三角形的两个锐角互余.
3.△ABC中,若∠A+∠B=∠C,则△ABC是( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
B
巩固练习
7.5 多边形的内角和(1)
巩固练习
7.5 多边形的内角和(1)
4.
基本运用
7.5 多边形的内角和(1)
1.
2.
3.
4.
C
直角
D
D
5.在△ABC中,∠A=40°∠B=∠C
求∠C的度数
7.5 多边形的内角和(1)
答:∠C的度数为
基本运用
基本运用
7.5 多边形的内角和(1)
6.
1
2
2
2
1
1
180°÷(1+2+2)=36°
180°÷(2+1+1)X2=90°
7.5 多边形的内角和(1)
7.
基本运用
8.已知:在△ABC中, ∠C=∠ABC=2∠A,BD 是AC边上的高。求∠DBC的度数。
答:∠DBC的度数为18°
7.5 多边形的内角和(1)
基本运用
解:
在△ABC中,∠C+∠ABC+∠A=180°
设∠A=x°,则∠C=∠ABC=2x0
∴x+2x+2x=180°
得:x=360
∴∠C=72°
在△BDC中,
∵∠BDC=90°
∴∠DBC=90°- ∠C
=90°-72°
=18°
1.如图△ABC中,∠ABC、∠ACB的平分线交于点O, ⑴若∠A=70°,求∠BOC。
A
B
C
O
2
1
╮
╰
解:∵三角形ABC中
∠ A+∠ABC+∠ACB =1800 ∠ A=70°
∴∠ABC+∠ACB=1800-∠ A=110°
又∵∠ABC、∠ACB的平分线交于点O
∴∠1=1/2∠ABC,∠2=1/2∠ACB
∴∠1+∠2=1/2∠ABC+1/2∠ACB
=1/2(∠ABC+∠ACB)
=1/2(1800-∠ A)
=1/2×110°=55°
又∵∠BOC+∠1+∠2=1800
∴∠BOC=1800-(∠1+∠2)=1800-55°=125°
180°-n°
1/2(180°-n°)
180°-1/2(180°-n°)=90°+1/2n°
⑵若∠A=n°,求∠BOC。
∠A=n°
综合运用
7.5 多边形的内角和(1)
综合运用
7.5 多边形的内角和(1)
2.
3.如图,AC、BD相交于点O,∠A与∠B的和等于∠C与∠D的和吗?为什么?
O
A
B
D
C
变式一:
如右图,∠A与∠B的和等于∠OCD与∠ODC的和吗?为什么?
解:
∵在△ABO中,
∠ A+∠B+∠1 =1800
∴ ∠A+∠B=1800 -∠1
∵在△CDO中,
∠C+∠D+∠2 = 1800
∴ ∠C+∠D =1800 -∠2
∵ ∠1 = ∠2
∴ ∠ A+∠B=∠C+∠D
1
2
综合运用
7.5 多边形的内角和(1)
8字型
变式二:
如图,D、E两点在∠BAC的内部,B、F、E、M四点在同一直线上,则∠A+∠ABF+∠ACD+∠D+∠DEF的度数为( )。
解:由8字型可知:
∠1+∠2=∠D+∠DEF
∵在△ABC中,
∠ A+∠ABC+∠ACB =1800
∴ ∠A+∠ABF+∠1+∠2+∠ACD=1800
即:
∠A+∠ABF+∠ACD+∠D+∠DEF=1800
2
1
╮
╰
1800
变化练习
7.5 多边形的内角和(1)
变式三:如图(1)是一个五角星,
∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数为( )。
A
C
D
E
B
解:由8字型可知:
∠1+∠2=∠B+∠E
∵在△ACD中,
∠ A+∠ACD+∠ADC =1800
∴ ∠A+∠ACE+∠1+∠2+∠ADB=1800
即:∠A+ ∠B+ ∠C+ ∠D+ ∠E=1800
2
1
╮
╰
1800
7.5 多边形的内角和(1)
变化练习
变式三:如图(1)是一个五角星,
∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数为( )。
A
C
D
E
B
解:由8字型可知:
∠1+∠2=∠B+∠E
∵在△ACD中,
∠ A+∠ACD+∠ADC =1800
∴ ∠A+∠ACE+∠1+∠2+∠ADB=1800
即:∠A+ ∠B+ ∠C+ ∠D+ ∠E=1800
2
1
╮
╰
A
变式四:
上图中的点A向下移到BE上时,五个角的和(即∠CAD+ ∠B+ ∠C+ ∠D+ ∠E )有无变化?如图(2)说明你的结论的正确性。
B
C
E
D
1800
无变化
7.5 多边形的内角和(1)
变化练习
1.如图,△ABC的内角平分线交于点O,若∠BOC=130°,则∠A的度数为( )
A 、100° B、 90° C、 80° D、70°
C
考题练习
7.5 多边形的内角和(1)
考题练习
7.5 多边形的内角和(1)
2.
考题练习
7.5 多边形的内角和(1)
3.
4.
6.
考题练习
7.5 多边形的内角和(1)
5.
数学文化
帕斯卡,法国数学家。早在300多年前这位科学家就已经发现了任何三角形的内角和是180度,而他当时才12 岁。
三角形的内角和是180°.
直角三角形的两个锐角互余.
课堂小结
(1)重点探究了三角形3个内角之间的关系
(2)由三角形3个内角之间的关系得到直
角三角形的一个性质:
(3)思想方法:
转化思想
(4)数学方法:
添辅助线
蓝用量角器量了量自己的内角和,就不再说话了!
你知道为什么吗?
情境问题
三角形的内角和是180度.
7.5 多边形的内角和(1)
探索三角形内角和定理
你有什么方法可以验证呢?
任意画一个三角形,量一量
探索三角形内角和定理
7.5 多边形的内角和(1)
锐角三角形
量一量
480
720
600
600+480+720=1800
探索三角形内角和定理
三角形的内角和是1800
7.5 多边形的内角和(1)
3
2
3
1
平角:1800
三角形的内角和是1800。
拼一拼
探索三角形内角和定理
7.5 多边形的内角和(1)
图2
A
B
C
A
B
M
探索三角形内角和定理
三角形的内角和是1800。
7.5 多边形的内角和(1)
在小学我们已经知道任意一个三角形三个内角的和等于180°,你还记得是怎么发现这个结论的吗?
A
B
C
折一折
探索三角形内角和定理
7.5 多边形的内角和(1)
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
折一折
探索三角形内角和定理
三角形的内角和是1800。
7.5 多边形的内角和(1)
解:过点A 作直线EF ,使EF∥BC.
∵ EF ∥BC (已知)
∴ ∠EAB = ∠B,
∠FAC = ∠C(两直线平行,内错角相等) .
已知:△ABC.∠A +∠B + ∠C = 180°吗.为什么?
A
B
C
E
F
∵ ∠EAB + ∠BAC + ∠CAF = 180°(平角定义)
∴ ∠A + ∠B + ∠C = 180°(等量代换).
三角形的内角和是1800。
探索三角形内角和定理
7.5 多边形的内角和(1)
已知:△ABC.∠A +∠B + ∠C = 180°吗.为什么?
A
B
C
E
F
探索三角形内角和定理
7.5 多边形的内角和(1)
解:延长BC到E
过点C 作直线CF ,使CF∥BA.
追问1 通过前面的验证过程,你能受到什么启发?你能用其他方法验证此定理吗?
C
A
B
1
2
3
4
5
l
探索三角形内角和定理
7.5 多边形的内角和(1)
解:延长BC到E
过点C 作直线CF ,使CF∥BA.
C
A
B
1
2
3
4
5
l
P
6
m
探索三角形内角和定理
追问2 通过前面的验证过程,你能受到什么启发?你能用其他方法验证此定理吗?
7.5 多边形的内角和(1)
C
A
B
1
2
3
4
5
l
P
6
m
n
探索三角形内角和定理
追问3 通过前面的验证过程,你能受到什么启发?你能用其他方法验证此定理吗?
7.5 多边形的内角和(1)
C
A
B
1
2
3
4
5
l
P
6
m
n
探索三角形内角和定理
追问4 通过前面的验证过程,你能受到什么启发?你能用其他方法验证此定理吗?
7.5 多边形的内角和(1)
为了说明的需要,在原来的图形上添画的线叫做辅助线。
方法小结
为了说明三个角的和为1800,转化为一个平角,这种转化思想是数学中的常用思想方法.
思路小结
探索三角形内角和定理
三角形的内角和是1800。
7.5 多边形的内角和(1)
在一个三角形的3个内角中,最多能有几个直角?最多能有几个钝角呢?为什么?
想一想
7.5 多边形的内角和(1)
三角形的内角和是1800。
1.根据下图填空:
(1)n= ; (2)x= ; (3)y= .
81°
72°
n°
(1)
x°
x°
(2)
∟
31°
y°
(3)
122°
27°
29°
59°
2.在直角△ABC中,∠C=90°,∠A+∠B= .
90°
7.5 多边形的内角和(1)
巩固练习
直角三角形的两个锐角互余.
3.△ABC中,若∠A+∠B=∠C,则△ABC是( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等腰三角形
B
巩固练习
7.5 多边形的内角和(1)
巩固练习
7.5 多边形的内角和(1)
4.
基本运用
7.5 多边形的内角和(1)
1.
2.
3.
4.
C
直角
D
D
5.在△ABC中,∠A=40°∠B=∠C
求∠C的度数
7.5 多边形的内角和(1)
答:∠C的度数为
基本运用
基本运用
7.5 多边形的内角和(1)
6.
1
2
2
2
1
1
180°÷(1+2+2)=36°
180°÷(2+1+1)X2=90°
7.5 多边形的内角和(1)
7.
基本运用
8.已知:在△ABC中, ∠C=∠ABC=2∠A,BD 是AC边上的高。求∠DBC的度数。
答:∠DBC的度数为18°
7.5 多边形的内角和(1)
基本运用
解:
在△ABC中,∠C+∠ABC+∠A=180°
设∠A=x°,则∠C=∠ABC=2x0
∴x+2x+2x=180°
得:x=360
∴∠C=72°
在△BDC中,
∵∠BDC=90°
∴∠DBC=90°- ∠C
=90°-72°
=18°
1.如图△ABC中,∠ABC、∠ACB的平分线交于点O, ⑴若∠A=70°,求∠BOC。
A
B
C
O
2
1
╮
╰
解:∵三角形ABC中
∠ A+∠ABC+∠ACB =1800 ∠ A=70°
∴∠ABC+∠ACB=1800-∠ A=110°
又∵∠ABC、∠ACB的平分线交于点O
∴∠1=1/2∠ABC,∠2=1/2∠ACB
∴∠1+∠2=1/2∠ABC+1/2∠ACB
=1/2(∠ABC+∠ACB)
=1/2(1800-∠ A)
=1/2×110°=55°
又∵∠BOC+∠1+∠2=1800
∴∠BOC=1800-(∠1+∠2)=1800-55°=125°
180°-n°
1/2(180°-n°)
180°-1/2(180°-n°)=90°+1/2n°
⑵若∠A=n°,求∠BOC。
∠A=n°
综合运用
7.5 多边形的内角和(1)
综合运用
7.5 多边形的内角和(1)
2.
3.如图,AC、BD相交于点O,∠A与∠B的和等于∠C与∠D的和吗?为什么?
O
A
B
D
C
变式一:
如右图,∠A与∠B的和等于∠OCD与∠ODC的和吗?为什么?
解:
∵在△ABO中,
∠ A+∠B+∠1 =1800
∴ ∠A+∠B=1800 -∠1
∵在△CDO中,
∠C+∠D+∠2 = 1800
∴ ∠C+∠D =1800 -∠2
∵ ∠1 = ∠2
∴ ∠ A+∠B=∠C+∠D
1
2
综合运用
7.5 多边形的内角和(1)
8字型
变式二:
如图,D、E两点在∠BAC的内部,B、F、E、M四点在同一直线上,则∠A+∠ABF+∠ACD+∠D+∠DEF的度数为( )。
解:由8字型可知:
∠1+∠2=∠D+∠DEF
∵在△ABC中,
∠ A+∠ABC+∠ACB =1800
∴ ∠A+∠ABF+∠1+∠2+∠ACD=1800
即:
∠A+∠ABF+∠ACD+∠D+∠DEF=1800
2
1
╮
╰
1800
变化练习
7.5 多边形的内角和(1)
变式三:如图(1)是一个五角星,
∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数为( )。
A
C
D
E
B
解:由8字型可知:
∠1+∠2=∠B+∠E
∵在△ACD中,
∠ A+∠ACD+∠ADC =1800
∴ ∠A+∠ACE+∠1+∠2+∠ADB=1800
即:∠A+ ∠B+ ∠C+ ∠D+ ∠E=1800
2
1
╮
╰
1800
7.5 多边形的内角和(1)
变化练习
变式三:如图(1)是一个五角星,
∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数为( )。
A
C
D
E
B
解:由8字型可知:
∠1+∠2=∠B+∠E
∵在△ACD中,
∠ A+∠ACD+∠ADC =1800
∴ ∠A+∠ACE+∠1+∠2+∠ADB=1800
即:∠A+ ∠B+ ∠C+ ∠D+ ∠E=1800
2
1
╮
╰
A
变式四:
上图中的点A向下移到BE上时,五个角的和(即∠CAD+ ∠B+ ∠C+ ∠D+ ∠E )有无变化?如图(2)说明你的结论的正确性。
B
C
E
D
1800
无变化
7.5 多边形的内角和(1)
变化练习
1.如图,△ABC的内角平分线交于点O,若∠BOC=130°,则∠A的度数为( )
A 、100° B、 90° C、 80° D、70°
C
考题练习
7.5 多边形的内角和(1)
考题练习
7.5 多边形的内角和(1)
2.
考题练习
7.5 多边形的内角和(1)
3.
4.
6.
考题练习
7.5 多边形的内角和(1)
5.
数学文化
帕斯卡,法国数学家。早在300多年前这位科学家就已经发现了任何三角形的内角和是180度,而他当时才12 岁。
三角形的内角和是180°.
直角三角形的两个锐角互余.
课堂小结
(1)重点探究了三角形3个内角之间的关系
(2)由三角形3个内角之间的关系得到直
角三角形的一个性质:
(3)思想方法:
转化思想
(4)数学方法:
添辅助线
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
