苏科版数学七年级下册 10.1 二元一次方程 课件(共20张PPT)
文档属性
| 名称 | 苏科版数学七年级下册 10.1 二元一次方程 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 23:59:12 | ||
图片预览








文档简介
(共20张PPT)
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
---笛卡儿[Descartes, Rene du Perron, 1596-1650 ]
(法国著名的哲学家、数学家、物理学家,解析几何之父 )
下列式子中是一元一次方程的为( )
①、④
10.1 二元一次方程
从“一元”到“二元”,建立了新的数学模型。
从“二元”到“一元”,用转化思想解决问题。
学习目标:
1、了解二元一次方程和它的解 的概念,体会这种新的模型表达两个变量关系的优点。
2、会检验一对数值是不是某个二元一次方程的解。
3、会将一个二元一次方程写成 用含一个未知数的代数式表示另一个未知数的形式。
自学内容:学案上问题一、问题二和想一想;
时间:5分钟
自学方法及要求:
1、认真研读,将问题中反映等量关系的句子划 “ ” ;关键词划“ ”;疑问的地
方划“ ?”。 独立、专注、安静。
2、完成后亮绿牌并知者加速。
3、自学有疑惑的地方可以亮红牌向老师求助。
有效学习——知识的生成
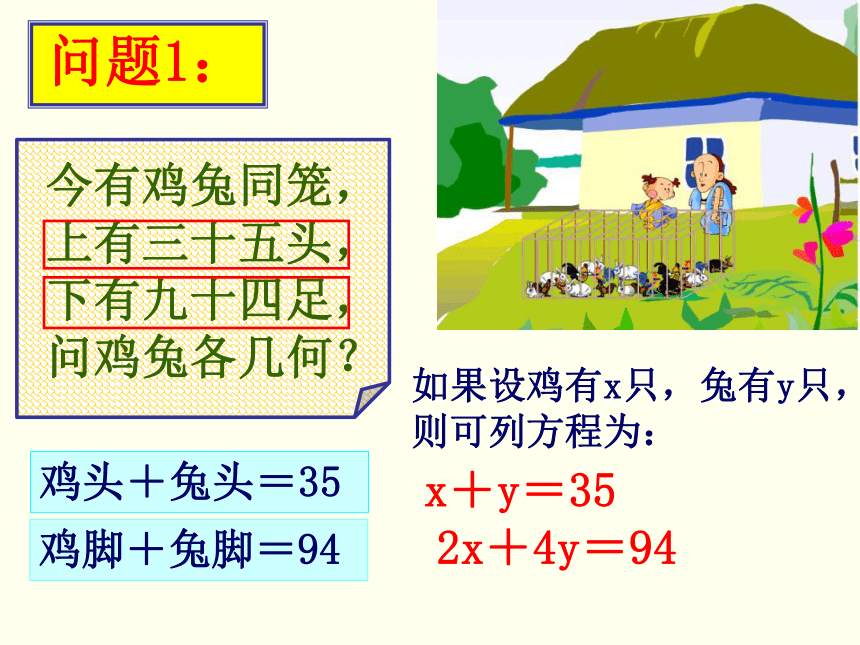
今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何?
鸡头+兔头=35
鸡脚+兔脚=94
如果设鸡有x只,兔有y只,
则可列方程为:
x+y=35
2x+4y=94
问题1:
篮球比赛规则规定:赢一场得2分,输一场得1分.在中学生篮球联赛中,某球队赛了若干场,积20分。问该球队赢了多少场 输了多少场
问题2:
如果设该队赢了x场,输了y场,那么:
2x+y=20
2x+y=2, x+y=35,
2x+4y=94, 2x+y=20.
思考下列方程的共同特点:
含有两个未知数, 且含有未知数的项的次数都是一次的方程。
二元一次方程:
想一想:
1、判断下列式子是否为二元一次方程?
(1) 3x+1=x2
(5) xy+y=2
(3) x=―+1
2
y
(6) -2y=0
3
x
(2) x2+y=0
(4) y+―x
2
1
检测反馈一
(√)
(×)
(×)
(×)
(×)
(×)
2、已知:5xm+7-2y2n-1=4是二元一次方程,m= , n= .
-6
知者加速: 若方程: 是关于x、y的二元一次方程,则m-n= .
检测反馈一:
1
x+3=12的解是:
你能写出二元一次方程x+y=12的解吗?
x=9
自学内容:书上P95议一议下面内容;
时间:2分钟
自学方法及要求:
1、认真研读,将问题中反映等量关系的句子划 “ ” ;关键词划“ ”;疑问的地方划“ ?”。 独立、专注、安静。
2、完成自学的同学思考知者加速。
3、自学有疑惑的地方可以亮红牌向老师求助。
有效学习——知识的生成
使二元一次方程两边的值相等的一对未知数的值叫做二元一次方程的一个解.
你能写出使二元一次方程x+y=12成立的未知数的值吗?
a
b
一个二元一次方程有无数个解。
1、下列3对数哪几对是二元一次方程2x+y=3的解?
x=-2
y=2
x=2
y=-1
x=
y=2
2、请写出一个以 为解的二元一次方程.
x=2
y=1
检测反馈二:
√
√
例如:x+y=3
3、一场中学生篮球比赛中,某球队得35分,其中2分球投中x 个,3分球投中y 个,没有罚球。
那么可得方程为 。
y
x
1
11
4
9
7
7
10
5
13
3
16
1
2x+3y=35
你能列出投中2分和3分球的个数的所有可能情况吗?
知者加速:等腰三角形ABC中,AB=x,BC=y,周长为12.
(1)列出关于x、y的二元一次方程;
(2)求出符合题意的所有整数解。
非负整数解
已知二元一次方程 2x+3y=35.
11和9;
(1)用关于x的代数式表示y.
(2)求当 x = 1,4时,对应的y的值, 并写出方程
2x+3y=35的这两个解.
合作交流:
x=1
y=11
x=4
y=9
回味无穷
(1)什么是二元一次方程?二元一次方程与一元一次方程的区别。
(2)什么是二元一次方程的解?怎样验证?
(3)如何用含一个未知数的代数式表示另一个未知数。
小结 拓展
建构模型:二元一次方程
1、判断下列式子哪些是二元一次方程,是的在( )
打“√”,不是的在( )打“×”。
(1)6x+3y=4( ) (2)7xy+y =9( )
(3)2x+y+1 ( ) (4)2x+8=y ( )
2、把二元一次方程2x-y =5写成用含x 的代数式表示
y 的形式是 。
3、甲种笔每枝2元,乙种笔每枝5元,现在某人买了x
枝甲种笔,y 枝乙种铅笔,共花了70元.
(1)列出关于x,y 的二元一次方程.
(2)如果x =5,那么y 的值是多少?
当堂检测:
√
×
×
√
y =2x- 5
2x+ 5 y =70
y =12
1、 书P95 习题10.1 T1、3(2)、4
2、《补充习题》P60
选做:《伴你学》P60 --61
作业:
为自己本节课的表现鼓掌
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
---笛卡儿[Descartes, Rene du Perron, 1596-1650 ]
(法国著名的哲学家、数学家、物理学家,解析几何之父 )
下列式子中是一元一次方程的为( )
①、④
10.1 二元一次方程
从“一元”到“二元”,建立了新的数学模型。
从“二元”到“一元”,用转化思想解决问题。
学习目标:
1、了解二元一次方程和它的解 的概念,体会这种新的模型表达两个变量关系的优点。
2、会检验一对数值是不是某个二元一次方程的解。
3、会将一个二元一次方程写成 用含一个未知数的代数式表示另一个未知数的形式。
自学内容:学案上问题一、问题二和想一想;
时间:5分钟
自学方法及要求:
1、认真研读,将问题中反映等量关系的句子划 “ ” ;关键词划“ ”;疑问的地
方划“ ?”。 独立、专注、安静。
2、完成后亮绿牌并知者加速。
3、自学有疑惑的地方可以亮红牌向老师求助。
有效学习——知识的生成
今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何?
鸡头+兔头=35
鸡脚+兔脚=94
如果设鸡有x只,兔有y只,
则可列方程为:
x+y=35
2x+4y=94
问题1:
篮球比赛规则规定:赢一场得2分,输一场得1分.在中学生篮球联赛中,某球队赛了若干场,积20分。问该球队赢了多少场 输了多少场
问题2:
如果设该队赢了x场,输了y场,那么:
2x+y=20
2x+y=2, x+y=35,
2x+4y=94, 2x+y=20.
思考下列方程的共同特点:
含有两个未知数, 且含有未知数的项的次数都是一次的方程。
二元一次方程:
想一想:
1、判断下列式子是否为二元一次方程?
(1) 3x+1=x2
(5) xy+y=2
(3) x=―+1
2
y
(6) -2y=0
3
x
(2) x2+y=0
(4) y+―x
2
1
检测反馈一
(√)
(×)
(×)
(×)
(×)
(×)
2、已知:5xm+7-2y2n-1=4是二元一次方程,m= , n= .
-6
知者加速: 若方程: 是关于x、y的二元一次方程,则m-n= .
检测反馈一:
1
x+3=12的解是:
你能写出二元一次方程x+y=12的解吗?
x=9
自学内容:书上P95议一议下面内容;
时间:2分钟
自学方法及要求:
1、认真研读,将问题中反映等量关系的句子划 “ ” ;关键词划“ ”;疑问的地方划“ ?”。 独立、专注、安静。
2、完成自学的同学思考知者加速。
3、自学有疑惑的地方可以亮红牌向老师求助。
有效学习——知识的生成
使二元一次方程两边的值相等的一对未知数的值叫做二元一次方程的一个解.
你能写出使二元一次方程x+y=12成立的未知数的值吗?
a
b
一个二元一次方程有无数个解。
1、下列3对数哪几对是二元一次方程2x+y=3的解?
x=-2
y=2
x=2
y=-1
x=
y=2
2、请写出一个以 为解的二元一次方程.
x=2
y=1
检测反馈二:
√
√
例如:x+y=3
3、一场中学生篮球比赛中,某球队得35分,其中2分球投中x 个,3分球投中y 个,没有罚球。
那么可得方程为 。
y
x
1
11
4
9
7
7
10
5
13
3
16
1
2x+3y=35
你能列出投中2分和3分球的个数的所有可能情况吗?
知者加速:等腰三角形ABC中,AB=x,BC=y,周长为12.
(1)列出关于x、y的二元一次方程;
(2)求出符合题意的所有整数解。
非负整数解
已知二元一次方程 2x+3y=35.
11和9;
(1)用关于x的代数式表示y.
(2)求当 x = 1,4时,对应的y的值, 并写出方程
2x+3y=35的这两个解.
合作交流:
x=1
y=11
x=4
y=9
回味无穷
(1)什么是二元一次方程?二元一次方程与一元一次方程的区别。
(2)什么是二元一次方程的解?怎样验证?
(3)如何用含一个未知数的代数式表示另一个未知数。
小结 拓展
建构模型:二元一次方程
1、判断下列式子哪些是二元一次方程,是的在( )
打“√”,不是的在( )打“×”。
(1)6x+3y=4( ) (2)7xy+y =9( )
(3)2x+y+1 ( ) (4)2x+8=y ( )
2、把二元一次方程2x-y =5写成用含x 的代数式表示
y 的形式是 。
3、甲种笔每枝2元,乙种笔每枝5元,现在某人买了x
枝甲种笔,y 枝乙种铅笔,共花了70元.
(1)列出关于x,y 的二元一次方程.
(2)如果x =5,那么y 的值是多少?
当堂检测:
√
×
×
√
y =2x- 5
2x+ 5 y =70
y =12
1、 书P95 习题10.1 T1、3(2)、4
2、《补充习题》P60
选做:《伴你学》P60 --61
作业:
为自己本节课的表现鼓掌
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
