苏科版数学七年级下册7.5多边形的内角和与外角和(1)课件 (共20张PPT)
文档属性
| 名称 | 苏科版数学七年级下册7.5多边形的内角和与外角和(1)课件 (共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 431.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:01:55 | ||
图片预览




文档简介
苏科版七年级下册
7.5多边形的内角和与外角和(1)
七年级数学
七年级数学
一、旧知回顾
平行线具有哪些性质?
1.两直线平行,同位角相等。
2.两直线平行,内错角相等。
3.两直线平行,同旁内角互补。
如图,已知a∥b.
则∠1=∠____(两直线平行,同位角相等)
∠1=∠____(两直线平行,内错角相等)
∠3+∠____=180°(两直线平行,同旁内角互补)
4
2
3
4
七年级数学
二、导入新课
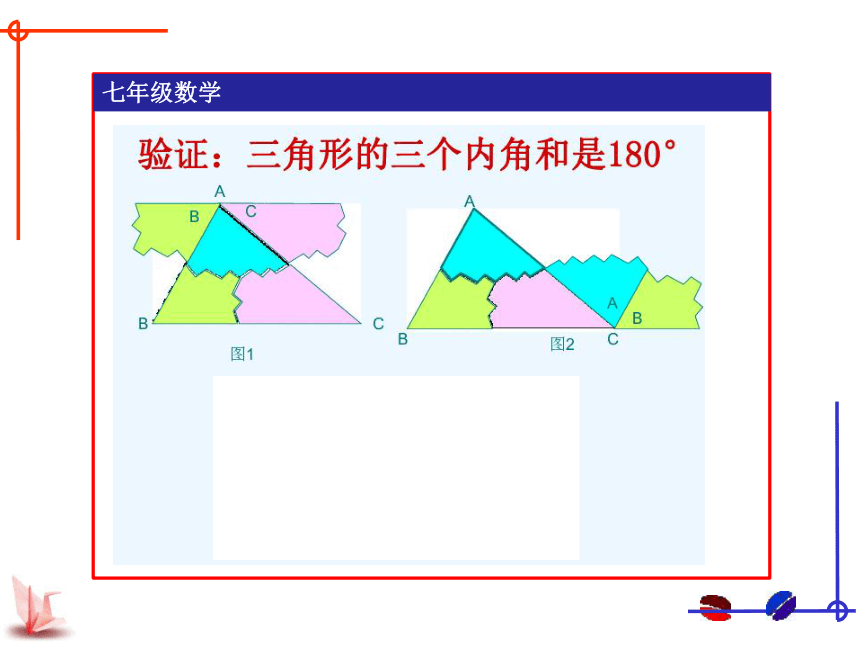
小学里学过的三角形的三个内角的和是180°
用量角器度量
七年级数学
七年级数学
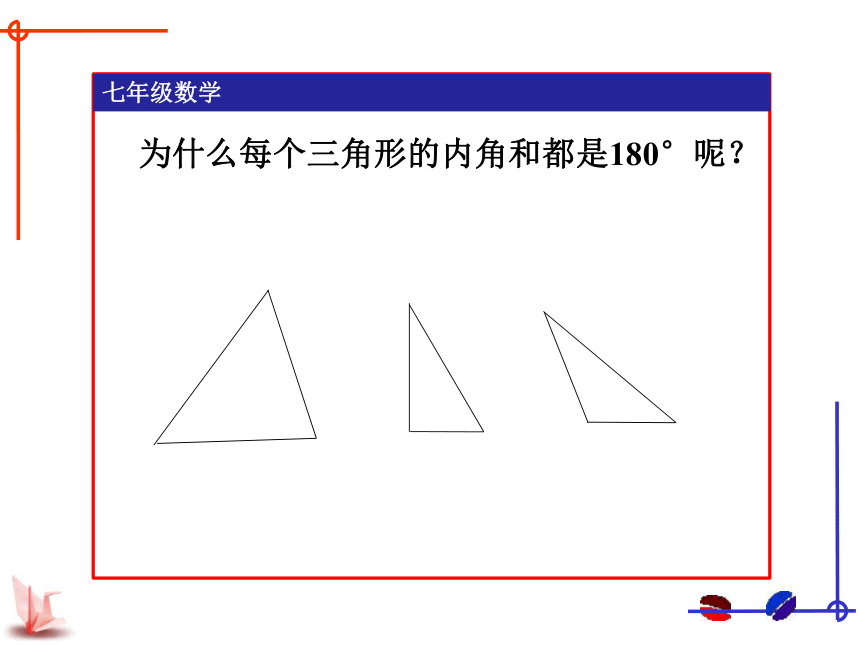
为什么每个三角形的内角和都是180°呢?
七年级数学
D
E
A
C
B
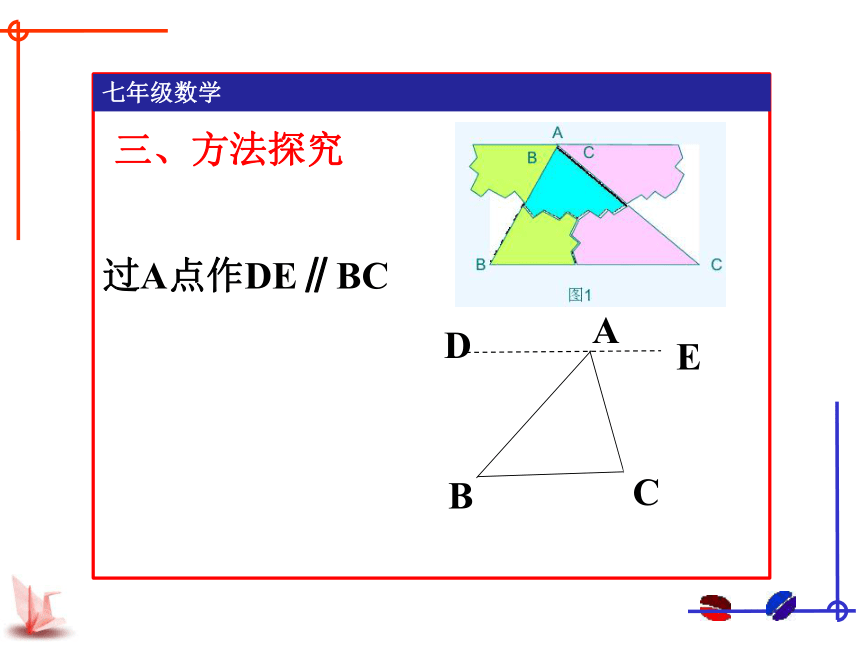
过A点作DE∥BC
三、方法探究
七年级数学
A
C
B
D
E
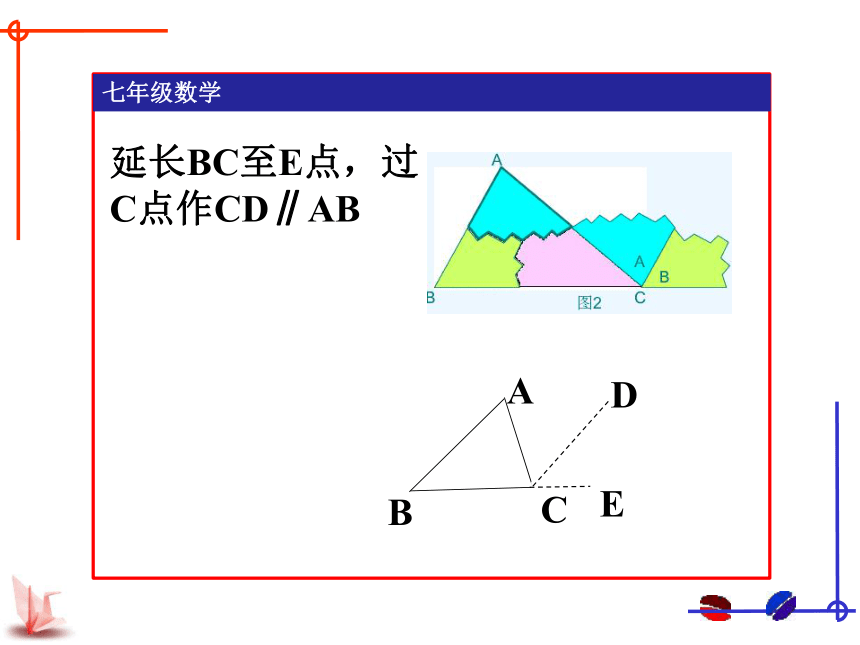
延长BC至E点,过C点作CD∥AB
七年级数学
A
C
B
E
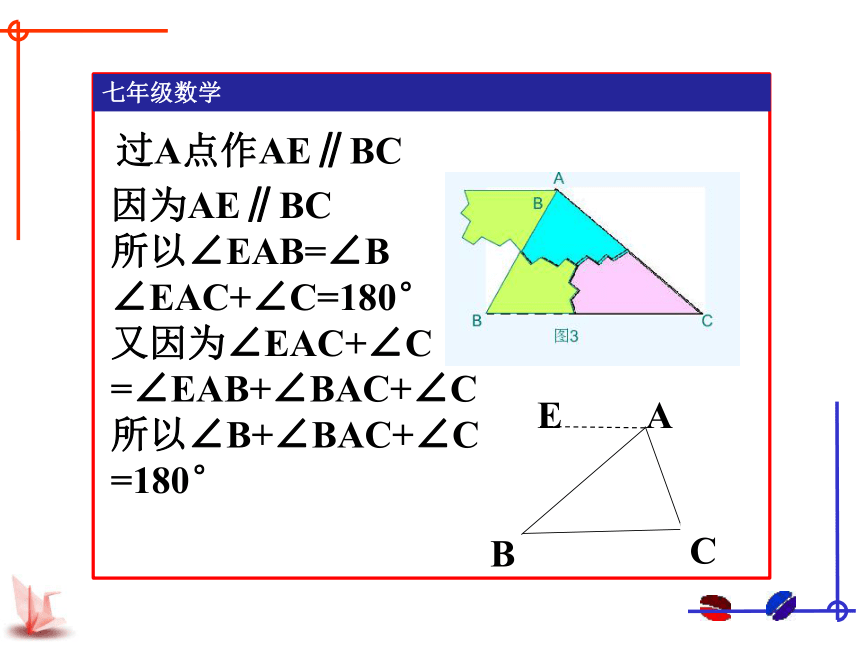
过A点作AE∥BC
因为AE∥BC
所以∠EAB=∠B ∠EAC+∠C=180°
又因为∠EAC+∠C
=∠EAB+∠BAC+∠C
所以∠B+∠BAC+∠C
=180°
七年级数学
四、典型例题
例1.在△ABC中,∠A=40°,∠B=∠C,求∠C的度数。
七年级数学
3.一个三角形能有两个内角是直角或钝角吗?
七年级数学
1. △ABC中,三个内角∠A、∠B、∠C的度数之比为2:3:4,求三个角的度数。
2. △ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A的度数是 ( )
A 40° B 60° C 80° D 90°
3. 在△ABC中,三个角∠A、∠B、∠C满足∠B-∠A=∠C-∠B,则∠B=_______
做一做
七年级数学
1. △ABC中,三个内角∠A、∠B、∠C的度数之比为2:3:4,求三个角的度数。
∠A= ×180°=40°
∠B= ×180°=60°
∠C= ×180°=80°
设∠A=2x°,∠B=3x°,∠C=4x°
七年级数学
2. △ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A的度数是 ( )
A 40° B 60° C 80° D 90°
A
注意:方程思想的运用
七年级数学
3. 在△ABC中,三个角∠A、∠B、∠C满足∠B-∠A=∠C-∠B,则∠B=_______
60°
由条件得:2∠B=∠A+∠C
∠B+∠A+∠C=180°
七年级数学
例2 如图,△ABC的角平分线BD、CE相交于点P,∠A=70°,求∠BPC的度数。
七年级数学
变式1:若题目中条件改为∠A=60°,求∠BPC的度数。
当∠A=n°呢?
变式2:若将原题∠A已知去掉,变成已知∠BPC=115°,求∠A的度数。
∠BPC=90°+ n°
∠A=50°
七年级数学
变式3:若题目中的BD、CE角平分线条件改为∠DBC= ∠ABC,∠ECB= ∠ACB,
∠A=n°,求∠BPC的度数
A
P
E
D
C
B
七年级数学
五、巩固与提高
在△ABC中,∠A=50°,∠B=30°,点D在边AB上,连接CD,若△ACD为直角三角形,则∠BCD的度数为___________.
60°或10°
A
C
B
D
D
注意本题要分类讨论
七年级数学
六、课堂小结
1.掌握三角形内角和是180°,并学会说理。
2.运用三角形内角和的知识解决具体问题。
3.体会各种数学思想方法的运用。
七年级数学
七、完成课后作业
7.5多边形的内角和与外角和(1)
七年级数学
七年级数学
一、旧知回顾
平行线具有哪些性质?
1.两直线平行,同位角相等。
2.两直线平行,内错角相等。
3.两直线平行,同旁内角互补。
如图,已知a∥b.
则∠1=∠____(两直线平行,同位角相等)
∠1=∠____(两直线平行,内错角相等)
∠3+∠____=180°(两直线平行,同旁内角互补)
4
2
3
4
七年级数学
二、导入新课
小学里学过的三角形的三个内角的和是180°
用量角器度量
七年级数学
七年级数学
为什么每个三角形的内角和都是180°呢?
七年级数学
D
E
A
C
B
过A点作DE∥BC
三、方法探究
七年级数学
A
C
B
D
E
延长BC至E点,过C点作CD∥AB
七年级数学
A
C
B
E
过A点作AE∥BC
因为AE∥BC
所以∠EAB=∠B ∠EAC+∠C=180°
又因为∠EAC+∠C
=∠EAB+∠BAC+∠C
所以∠B+∠BAC+∠C
=180°
七年级数学
四、典型例题
例1.在△ABC中,∠A=40°,∠B=∠C,求∠C的度数。
七年级数学
3.一个三角形能有两个内角是直角或钝角吗?
七年级数学
1. △ABC中,三个内角∠A、∠B、∠C的度数之比为2:3:4,求三个角的度数。
2. △ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A的度数是 ( )
A 40° B 60° C 80° D 90°
3. 在△ABC中,三个角∠A、∠B、∠C满足∠B-∠A=∠C-∠B,则∠B=_______
做一做
七年级数学
1. △ABC中,三个内角∠A、∠B、∠C的度数之比为2:3:4,求三个角的度数。
∠A= ×180°=40°
∠B= ×180°=60°
∠C= ×180°=80°
设∠A=2x°,∠B=3x°,∠C=4x°
七年级数学
2. △ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A的度数是 ( )
A 40° B 60° C 80° D 90°
A
注意:方程思想的运用
七年级数学
3. 在△ABC中,三个角∠A、∠B、∠C满足∠B-∠A=∠C-∠B,则∠B=_______
60°
由条件得:2∠B=∠A+∠C
∠B+∠A+∠C=180°
七年级数学
例2 如图,△ABC的角平分线BD、CE相交于点P,∠A=70°,求∠BPC的度数。
七年级数学
变式1:若题目中条件改为∠A=60°,求∠BPC的度数。
当∠A=n°呢?
变式2:若将原题∠A已知去掉,变成已知∠BPC=115°,求∠A的度数。
∠BPC=90°+ n°
∠A=50°
七年级数学
变式3:若题目中的BD、CE角平分线条件改为∠DBC= ∠ABC,∠ECB= ∠ACB,
∠A=n°,求∠BPC的度数
A
P
E
D
C
B
七年级数学
五、巩固与提高
在△ABC中,∠A=50°,∠B=30°,点D在边AB上,连接CD,若△ACD为直角三角形,则∠BCD的度数为___________.
60°或10°
A
C
B
D
D
注意本题要分类讨论
七年级数学
六、课堂小结
1.掌握三角形内角和是180°,并学会说理。
2.运用三角形内角和的知识解决具体问题。
3.体会各种数学思想方法的运用。
七年级数学
七、完成课后作业
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
