苏科版数学七年级下册第七章平面图形的认识(二) 小结与思考课件 (共19张PPT)
文档属性
| 名称 | 苏科版数学七年级下册第七章平面图形的认识(二) 小结与思考课件 (共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 212.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:02:17 | ||
图片预览


文档简介
苏科版七年级下册
第7章 平面图形的认识(二)
小结与思考
七年级数学
七年级数学
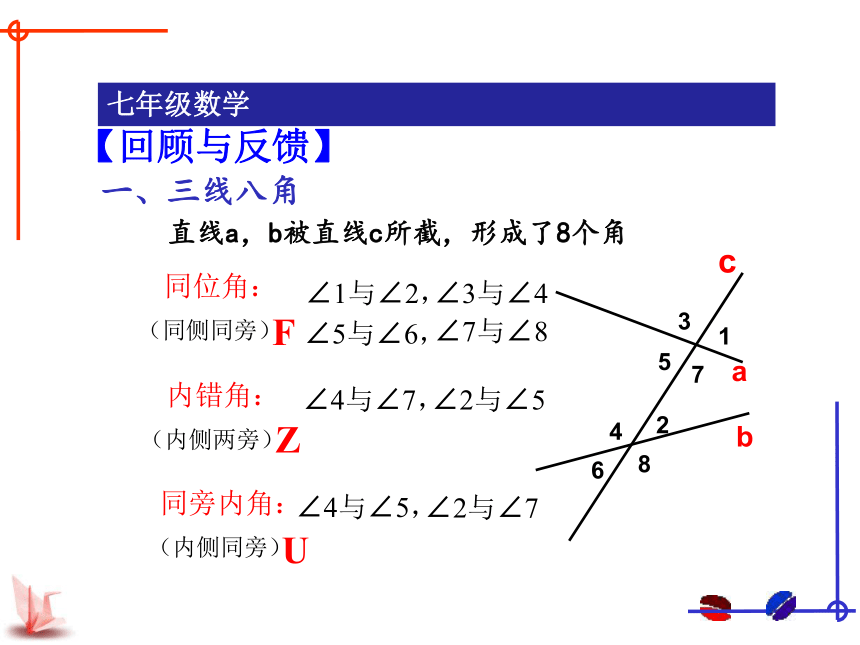
一、三线八角
直线a,b被直线c所截,形成了8个角
【回顾与反馈】
1
3
5
7
2
4
6
8
a
b
c
同位角:
∠1与∠2,
∠3与∠4
∠5与∠6,
∠7与∠8
(同侧同旁)
内错角:
∠4与∠7,
∠2与∠5
(内侧两旁)
同旁内角:
∠4与∠5,
∠2与∠7
(内侧同旁)
F
Z
U
七年级数学
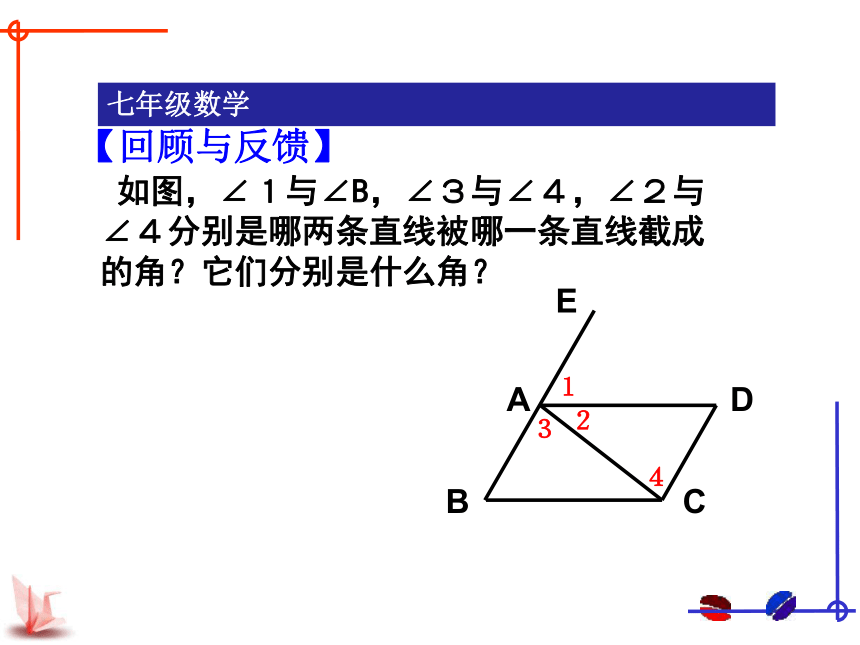
如图,∠1与∠B,∠3与∠4,∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?
【回顾与反馈】
1
2
3
4
A
B
C
D
E
七年级数学
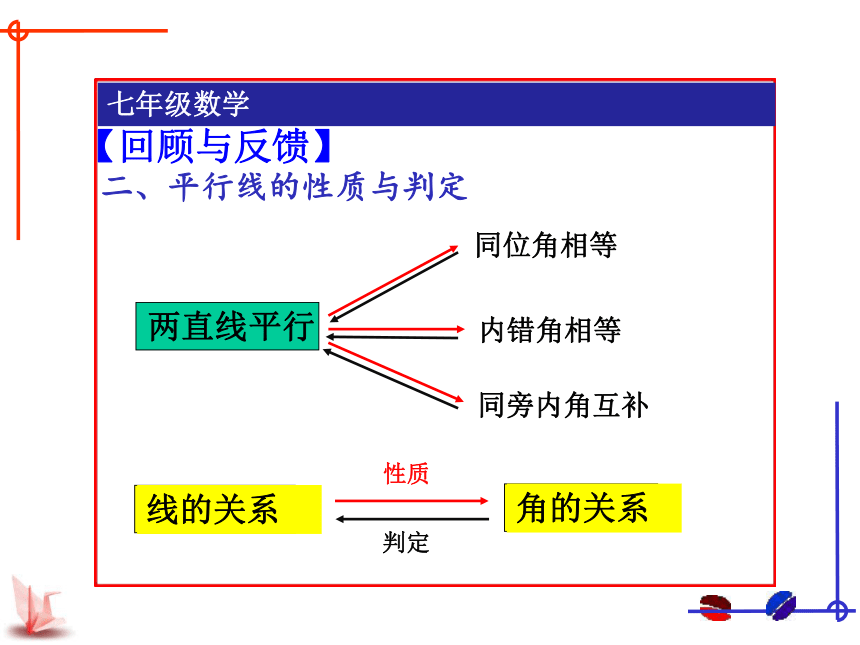
二、平行线的性质与判定
【回顾与反馈】
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
性质
判定
七年级数学
【回顾与反馈】
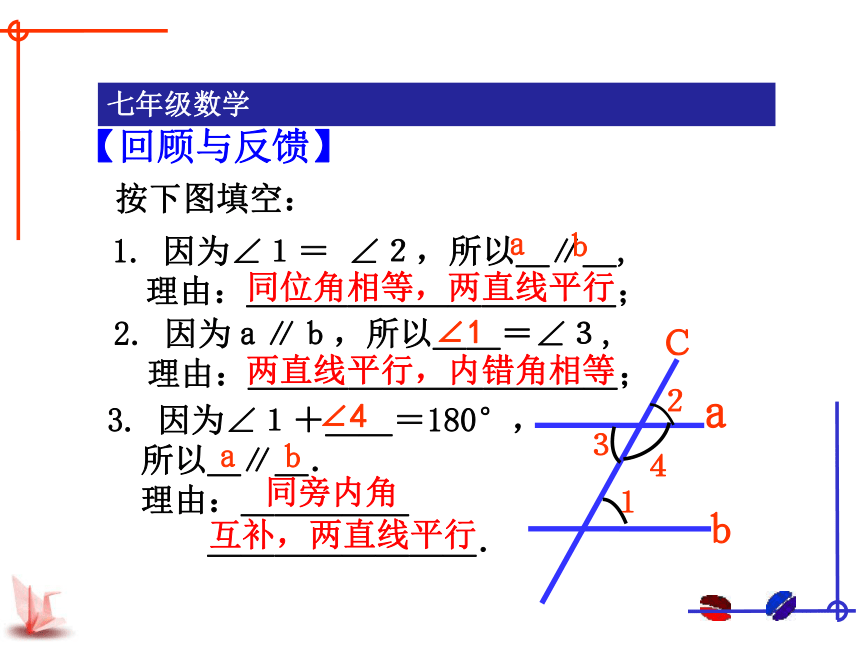
按下图填空:
1. 因为∠1= ∠2,所以_∥_,
理由:___________;
2. 因为a∥b,所以__=∠3,
理由:___________;
3. 因为∠1+__=180°,
所以_∥_.
理由:_____
________.
a
b
C
1
2
3
4
a
b
同位角相等,两直线平行
两直线平行,内错角相等
同旁内角
互补,两直线平行
∠1
∠4
a
b
七年级数学
三、图形的平移
【回顾与反馈】
1. 在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移。
2. 平移不改变图形的 和 。
3. 一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等。
形状
大小
七年级数学
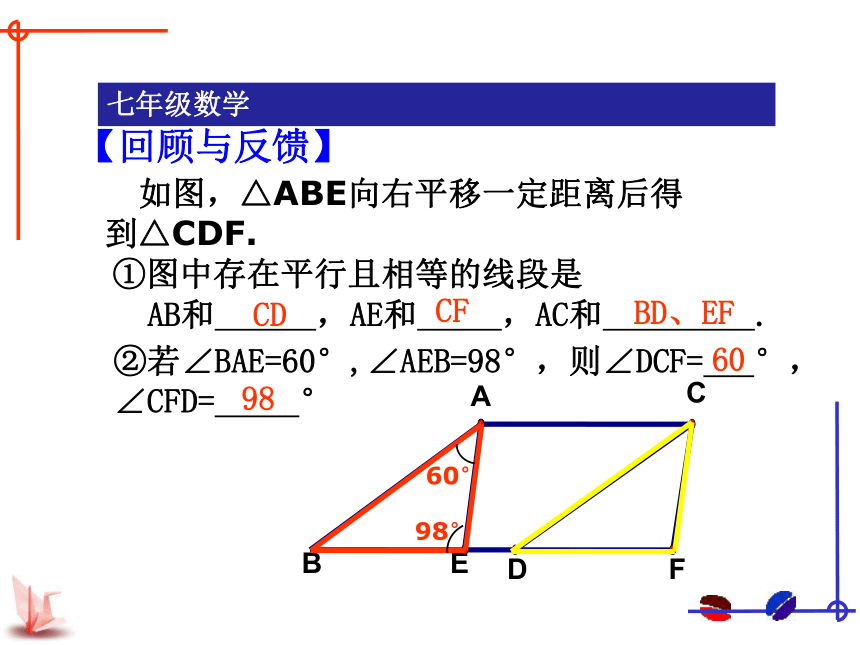
如图,△ABE向右平移一定距离后得到△CDF.
【回顾与反馈】
①图中存在平行且相等的线段是
AB和 ,AE和 ,AC和 .
②若∠BAE=60°,∠AEB=98°,则∠DCF= °, ∠CFD= °
D
E
B
A
C
F
60°
98°
CD
CF
BD、EF
60
98
七年级数学
四、认识三角形
【回顾与反馈】
1. 三角形的分类:
按角分
钝角三角形
直角三角形
锐角三角形
按边分
等腰三角形
不等边三角形
(等边三角形)
七年级数学
四、认识三角形
【回顾与反馈】
2. 三角形的三条重要线段:
(1)角平分线
(2)中线
(3) 高线
思考:三角形的角平分线、中线、高线分别有几条?它们是如何分布的?它们的交点情况如何呢?
七年级数学
四、认识三角形
【回顾与反馈】
3. 三角形的有关知识:
①三角形的内角和等于 。
②直角三角形的两个锐角 。
③三角形的一个外角等于 。
④三角形的任意两边之和 第三边
(两边之差的绝对值<第三边<两边之和)
180°
互余
与它不相邻的两个内角的和
大于
七年级数学
【回顾与反馈】
1.有长为3、5、7、10的四根木条,从中选三根能摆
出( )个三角形
A 、1 B、2 C、3 D、4
2.在△ABC中,∠A= 1/2 ∠B= 1/3 ∠C,则∠A= °
∠B= °,∠C= °。
3.如图,CD、CE是△ABC的高和角平分线,∠A=40°, ∠B=60°,求∠DCE的度数.
B
30
60
90
解:∵ ∠A=40°, ∠B=60°
∴∠ACB=180°-40°-60°=80°
又∵CE平分∠ACB
∴∠BCE=1/2∠ACB=40°
又∵CD⊥AB, ∠B=60°
∴∠BCD=30° ∴∠DCE=∠BCE-∠BCD=10°
七年级数学
五、多边形的有关知识
【回顾与反馈】
1. n边形的内角和等于 。
2. n边形的外角和等于 。
360°
(n-2)×180°
七年级数学
【回顾与反馈】
1. 若一个多边形的内角和是外角和的3.5倍,则此多边形的边数是( )
A、7 B、14 C、9 D、18
2.如果一个八边形的内角都相等,那么它的每
个内角等于多少度?
每一个外角:360°÷8=45°
每一个内角:180°-45°=135°
(n-2)×180°=360°×3.5
C
七年级数学
【小试牛刀】
1.下列说法中错误的是 ( ) A.三角形的中线、角平分线、高线都是线段 B.任意三角形的内角和都是180°
C.三角形按边分可分为不等边三角形和等腰三角形
D.三角形的一个外角大于任何一个内角
2.如图,∠1=∠2=45°,∠3=70°,
则∠4的度数是 ( )
A.45° B.70°
C.110° D.135°
D
C
七年级数学
【小试牛刀】
3.如图,在△ABC中, ∠A=62°, ∠1=20°, ∠2=35°.
求∠BDC的度数
解:在△ABC中,
得∠ABC+ ∠ACB=180°-62°=118°
由∠1=20°, ∠2=35°,
得∠DBC+ ∠DCB=118°-(20°+35°)=63°
在△DBC中,
得∠BDC=180°-( ∠ DBC+ ∠ DCB)
=180°-63°=117°
七年级数学
【拓展延伸】
多边形相关的知识点:
多边形的对角线:连接多边形不相邻的两个顶点的线段,
叫做多边形的对角线.
如图,AC、AD是五边形ABCDE的对角线
A
B
C
D
E
七年级数学
【拓展延伸】
观察并回答:
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
四边形ABCD中,过顶点A可以画___条对角线
五边形ABCDE中,过顶点A可以画___条对角线
六边形ABCDEF中,过顶点A可以画___条对角线
由上图可知:
1
2
3
七年级数学
【拓展延伸】
相信你能行!
(1)如图,n边形中,过顶点A1可以画__ _条
对角线,它们分别是:________________;过顶
点A2可以画_______条对角线;过顶点A3可以画
________条对角线.
(2)过顶点A1的对角线与过顶点A2的对角线有相同的吗?
过顶点A1的对角线与过顶点A3的对角线有相同的吗?
(3)在此基础上,你能发现n边形有多少条对角了吗?
A2
A1
A3
A4
A5
A6
An
(n-3)
A1A3,A1A4……A1An-1
(n-3)
(n-3)
没有
有 A1A3和A3A1
七年级数学
通过本节课的学习,你有哪些收获?还有哪些困惑?请与其他同学交流.
课堂小结
第7章 平面图形的认识(二)
小结与思考
七年级数学
七年级数学
一、三线八角
直线a,b被直线c所截,形成了8个角
【回顾与反馈】
1
3
5
7
2
4
6
8
a
b
c
同位角:
∠1与∠2,
∠3与∠4
∠5与∠6,
∠7与∠8
(同侧同旁)
内错角:
∠4与∠7,
∠2与∠5
(内侧两旁)
同旁内角:
∠4与∠5,
∠2与∠7
(内侧同旁)
F
Z
U
七年级数学
如图,∠1与∠B,∠3与∠4,∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?
【回顾与反馈】
1
2
3
4
A
B
C
D
E
七年级数学
二、平行线的性质与判定
【回顾与反馈】
两直线平行
同位角相等
内错角相等
同旁内角互补
线的关系
角的关系
性质
判定
七年级数学
【回顾与反馈】
按下图填空:
1. 因为∠1= ∠2,所以_∥_,
理由:___________;
2. 因为a∥b,所以__=∠3,
理由:___________;
3. 因为∠1+__=180°,
所以_∥_.
理由:_____
________.
a
b
C
1
2
3
4
a
b
同位角相等,两直线平行
两直线平行,内错角相等
同旁内角
互补,两直线平行
∠1
∠4
a
b
七年级数学
三、图形的平移
【回顾与反馈】
1. 在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移。
2. 平移不改变图形的 和 。
3. 一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等。
形状
大小
七年级数学
如图,△ABE向右平移一定距离后得到△CDF.
【回顾与反馈】
①图中存在平行且相等的线段是
AB和 ,AE和 ,AC和 .
②若∠BAE=60°,∠AEB=98°,则∠DCF= °, ∠CFD= °
D
E
B
A
C
F
60°
98°
CD
CF
BD、EF
60
98
七年级数学
四、认识三角形
【回顾与反馈】
1. 三角形的分类:
按角分
钝角三角形
直角三角形
锐角三角形
按边分
等腰三角形
不等边三角形
(等边三角形)
七年级数学
四、认识三角形
【回顾与反馈】
2. 三角形的三条重要线段:
(1)角平分线
(2)中线
(3) 高线
思考:三角形的角平分线、中线、高线分别有几条?它们是如何分布的?它们的交点情况如何呢?
七年级数学
四、认识三角形
【回顾与反馈】
3. 三角形的有关知识:
①三角形的内角和等于 。
②直角三角形的两个锐角 。
③三角形的一个外角等于 。
④三角形的任意两边之和 第三边
(两边之差的绝对值<第三边<两边之和)
180°
互余
与它不相邻的两个内角的和
大于
七年级数学
【回顾与反馈】
1.有长为3、5、7、10的四根木条,从中选三根能摆
出( )个三角形
A 、1 B、2 C、3 D、4
2.在△ABC中,∠A= 1/2 ∠B= 1/3 ∠C,则∠A= °
∠B= °,∠C= °。
3.如图,CD、CE是△ABC的高和角平分线,∠A=40°, ∠B=60°,求∠DCE的度数.
B
30
60
90
解:∵ ∠A=40°, ∠B=60°
∴∠ACB=180°-40°-60°=80°
又∵CE平分∠ACB
∴∠BCE=1/2∠ACB=40°
又∵CD⊥AB, ∠B=60°
∴∠BCD=30° ∴∠DCE=∠BCE-∠BCD=10°
七年级数学
五、多边形的有关知识
【回顾与反馈】
1. n边形的内角和等于 。
2. n边形的外角和等于 。
360°
(n-2)×180°
七年级数学
【回顾与反馈】
1. 若一个多边形的内角和是外角和的3.5倍,则此多边形的边数是( )
A、7 B、14 C、9 D、18
2.如果一个八边形的内角都相等,那么它的每
个内角等于多少度?
每一个外角:360°÷8=45°
每一个内角:180°-45°=135°
(n-2)×180°=360°×3.5
C
七年级数学
【小试牛刀】
1.下列说法中错误的是 ( ) A.三角形的中线、角平分线、高线都是线段 B.任意三角形的内角和都是180°
C.三角形按边分可分为不等边三角形和等腰三角形
D.三角形的一个外角大于任何一个内角
2.如图,∠1=∠2=45°,∠3=70°,
则∠4的度数是 ( )
A.45° B.70°
C.110° D.135°
D
C
七年级数学
【小试牛刀】
3.如图,在△ABC中, ∠A=62°, ∠1=20°, ∠2=35°.
求∠BDC的度数
解:在△ABC中,
得∠ABC+ ∠ACB=180°-62°=118°
由∠1=20°, ∠2=35°,
得∠DBC+ ∠DCB=118°-(20°+35°)=63°
在△DBC中,
得∠BDC=180°-( ∠ DBC+ ∠ DCB)
=180°-63°=117°
七年级数学
【拓展延伸】
多边形相关的知识点:
多边形的对角线:连接多边形不相邻的两个顶点的线段,
叫做多边形的对角线.
如图,AC、AD是五边形ABCDE的对角线
A
B
C
D
E
七年级数学
【拓展延伸】
观察并回答:
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
四边形ABCD中,过顶点A可以画___条对角线
五边形ABCDE中,过顶点A可以画___条对角线
六边形ABCDEF中,过顶点A可以画___条对角线
由上图可知:
1
2
3
七年级数学
【拓展延伸】
相信你能行!
(1)如图,n边形中,过顶点A1可以画__ _条
对角线,它们分别是:________________;过顶
点A2可以画_______条对角线;过顶点A3可以画
________条对角线.
(2)过顶点A1的对角线与过顶点A2的对角线有相同的吗?
过顶点A1的对角线与过顶点A3的对角线有相同的吗?
(3)在此基础上,你能发现n边形有多少条对角了吗?
A2
A1
A3
A4
A5
A6
An
(n-3)
A1A3,A1A4……A1An-1
(n-3)
(n-3)
没有
有 A1A3和A3A1
七年级数学
通过本节课的学习,你有哪些收获?还有哪些困惑?请与其他同学交流.
课堂小结
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
