苏科版八年级下册数学《12.1二次根式》 (共27张PPT)
文档属性
| 名称 | 苏科版八年级下册数学《12.1二次根式》 (共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 10:29:10 | ||
图片预览








文档简介
12.1二次根式
2.什么是一个数的算术平方根?如何表示?
的算术平方根是
1.什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于 ,则这个数叫做 的平方根 的平方根是
正数的正的平方根叫做它的算术平方根。0的算术平方根是0.
回顾旧知
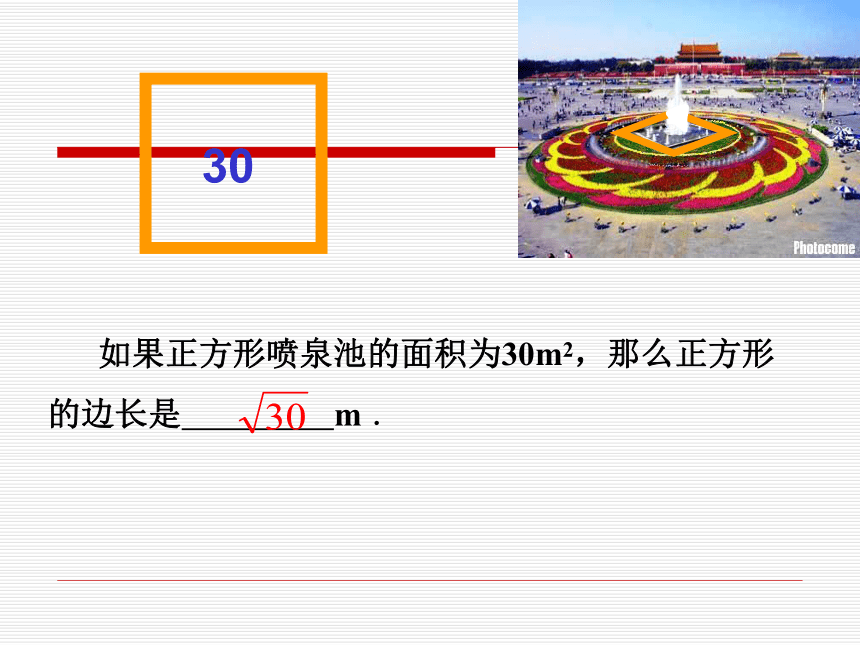
这是天安门广场前的大型音乐喷泉的图片,非常美丽壮观,仔细观察发现:水域部分是正方形,外围是圆.
情境导入
如果正方形喷泉池的面积为30m2,那么正方形的边长是 m .
30
如果圆形花坛的面积为S,那么这个圆的半径是 .
A
B
这是同学们常见的某跨江斜拉索大桥,若其中一根钢索的水平距离是9m,垂直距离是αm.同学们知道这根钢索的长度是多少m?
A
C
a米
B
9米
?
.●
.●
.●
AB=_____米
A
B
形如 (a≥0)的式子叫做二次根式,其中,a叫被开方数.
观察这些式子有什么共同特征?
探索活动一
议一议
(1)当a<0时, 有意义吗?为什么?
(2)当a≥0时, 可能为负数吗?为什么?
议一议
具有双重非负性
例1 下列哪些式子是二次根式?为什么?
解:(1)、(2)是二次根式.
探索活动一
(1) ;(2) ;
(3) ; (4) (x、y异号).
说一说,下列各式是二次根式吗?
解:(1)、(3)、(4)是二次根式 .
练一练
(3) ; (4) (m≤0).
(1) ; (2) ;
归归
第一:有二次根号
二次根式应满足两个条件:
第二:被开方数是非负数
归纳总结
例2 x是怎样的实数时,下列式子在实数范围内有意义?
探索活动二
(3) ; (4) .
(1) ; (2) ;
∴当x为任意实数时,式子 在
实数范围内有意义.
解:由x+1≥0,则x≥-1.
∴当x≥-1时,式子 在实数范围内有意义.
解:∵在实数范围内,不论x取什么值, 恒有x2 +2>0,
(1)
(2)
解:∵在实数范围内,不论x取什么值,恒有
-x2≤0;
又∵二次根式的被开方数大于等于零;
∴当x=0时, 式子 在实数范围内有意义.
∴ -x2=0,即x=0;
(3)
解:由题目条件:
解①得:x≤ ;
解②得:x≠ .
∴不等式组的解集为:x< .
∴当x< 时, 式子 在实数范围内有意义.
(4)
归纳总结
如何确定字母的值,使含有二次根式的式子在实数范围内有意义?
要使下列各式有意义,χ应是怎样的实数?
(1) (2)
(3) (4) +
练一练
练一练
探索活动三
1. 的意义是什么?你会计算( )2吗?类似地,( )2、( )2、( )2、( )2的结果是什么?类比猜想:当a≥0时,( )2的结果是什么?
例3 计算:
(1)( )2; (2)( )2;
(3)( )2(a+b≥0).
探究活动三
练一练
计算:
(2)
(1)
(3) (4)
硕果累累
一路下来,我们结识了很多新知识,你能谈谈自己的收获吗?说一说,让大家一起来分享。
形如 (a≥0)
的式子叫做二次根式
1.二次根式的定义:
2.二次根式 有意义的条件:
3.二次根式的基本性质:
当a≥0时,
a≥0
归纳总结
D
1.下列式子中,一定是二次根式的是( )
A. B. C. D.
2.若式子 有意义,那么χ的取值范围是( )
A. B. C. D.一切实数
3.要使 有意义,则χ的取值范围是( )
A. B. C. χ> D.x<
4.要使 有意义,则实数χ的取值范围是( )
A. B. >-3且 C. D. 且
5、若 ,则χ=______
A
C
D
-3
反馈训练
1.课本P151第1、2题.
课外作业
2.若实数x、y满足 +(y+2)2=0,
求y x 的值.
3.在实数范围内分解因式:
(1) -3 (2) -5χ
4.已知y= + -3,那么 的值是( )
A.-6 B. -9 C. 6 D.9
谢 谢 大 家
2.什么是一个数的算术平方根?如何表示?
的算术平方根是
1.什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于 ,则这个数叫做 的平方根 的平方根是
正数的正的平方根叫做它的算术平方根。0的算术平方根是0.
回顾旧知
这是天安门广场前的大型音乐喷泉的图片,非常美丽壮观,仔细观察发现:水域部分是正方形,外围是圆.
情境导入
如果正方形喷泉池的面积为30m2,那么正方形的边长是 m .
30
如果圆形花坛的面积为S,那么这个圆的半径是 .
A
B
这是同学们常见的某跨江斜拉索大桥,若其中一根钢索的水平距离是9m,垂直距离是αm.同学们知道这根钢索的长度是多少m?
A
C
a米
B
9米
?
.●
.●
.●
AB=_____米
A
B
形如 (a≥0)的式子叫做二次根式,其中,a叫被开方数.
观察这些式子有什么共同特征?
探索活动一
议一议
(1)当a<0时, 有意义吗?为什么?
(2)当a≥0时, 可能为负数吗?为什么?
议一议
具有双重非负性
例1 下列哪些式子是二次根式?为什么?
解:(1)、(2)是二次根式.
探索活动一
(1) ;(2) ;
(3) ; (4) (x、y异号).
说一说,下列各式是二次根式吗?
解:(1)、(3)、(4)是二次根式 .
练一练
(3) ; (4) (m≤0).
(1) ; (2) ;
归归
第一:有二次根号
二次根式应满足两个条件:
第二:被开方数是非负数
归纳总结
例2 x是怎样的实数时,下列式子在实数范围内有意义?
探索活动二
(3) ; (4) .
(1) ; (2) ;
∴当x为任意实数时,式子 在
实数范围内有意义.
解:由x+1≥0,则x≥-1.
∴当x≥-1时,式子 在实数范围内有意义.
解:∵在实数范围内,不论x取什么值, 恒有x2 +2>0,
(1)
(2)
解:∵在实数范围内,不论x取什么值,恒有
-x2≤0;
又∵二次根式的被开方数大于等于零;
∴当x=0时, 式子 在实数范围内有意义.
∴ -x2=0,即x=0;
(3)
解:由题目条件:
解①得:x≤ ;
解②得:x≠ .
∴不等式组的解集为:x< .
∴当x< 时, 式子 在实数范围内有意义.
(4)
归纳总结
如何确定字母的值,使含有二次根式的式子在实数范围内有意义?
要使下列各式有意义,χ应是怎样的实数?
(1) (2)
(3) (4) +
练一练
练一练
探索活动三
1. 的意义是什么?你会计算( )2吗?类似地,( )2、( )2、( )2、( )2的结果是什么?类比猜想:当a≥0时,( )2的结果是什么?
例3 计算:
(1)( )2; (2)( )2;
(3)( )2(a+b≥0).
探究活动三
练一练
计算:
(2)
(1)
(3) (4)
硕果累累
一路下来,我们结识了很多新知识,你能谈谈自己的收获吗?说一说,让大家一起来分享。
形如 (a≥0)
的式子叫做二次根式
1.二次根式的定义:
2.二次根式 有意义的条件:
3.二次根式的基本性质:
当a≥0时,
a≥0
归纳总结
D
1.下列式子中,一定是二次根式的是( )
A. B. C. D.
2.若式子 有意义,那么χ的取值范围是( )
A. B. C. D.一切实数
3.要使 有意义,则χ的取值范围是( )
A. B. C. χ> D.x<
4.要使 有意义,则实数χ的取值范围是( )
A. B. >-3且 C. D. 且
5、若 ,则χ=______
A
C
D
-3
反馈训练
1.课本P151第1、2题.
课外作业
2.若实数x、y满足 +(y+2)2=0,
求y x 的值.
3.在实数范围内分解因式:
(1) -3 (2) -5χ
4.已知y= + -3,那么 的值是( )
A.-6 B. -9 C. 6 D.9
谢 谢 大 家
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
