苏科版七年级数学下册9.4乘法公式课件(共16张ppt)
文档属性
| 名称 | 苏科版七年级数学下册9.4乘法公式课件(共16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 668.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 10:41:29 | ||
图片预览






文档简介
给我最大快乐的,不是已懂的知识,
而是不断的学习.----高斯
小明同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,王捷就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你真是个神童!”王捷同学说:“过奖了,我只是利用了在数学上刚学过的一个公式.”
1计算:
⑴ (x+1)(x-1)=______ ;
⑵ (m+2)(m-2)=_____ ;
⑶ (2x+3)(2x-3)=______.
(4) (a+2b)(a-2b)=______
观察上述算式,等号左边有什么规律?
观察计算结果, 你又发现了什么规律?
- 1
- 4
- 9
2猜想:(a + b)(a- b)=——————.
a2-b2
a2-4b2
(a+b)(a-b)
3证明:(1)代数
角度
(a + b)(a- b)=a2-b2.
∴(a + b)(a- b)=a2-b2.
(多项式乘法法则)
(合并同类项)
`
a
a
b
a2
b2
-
b
a
a
b
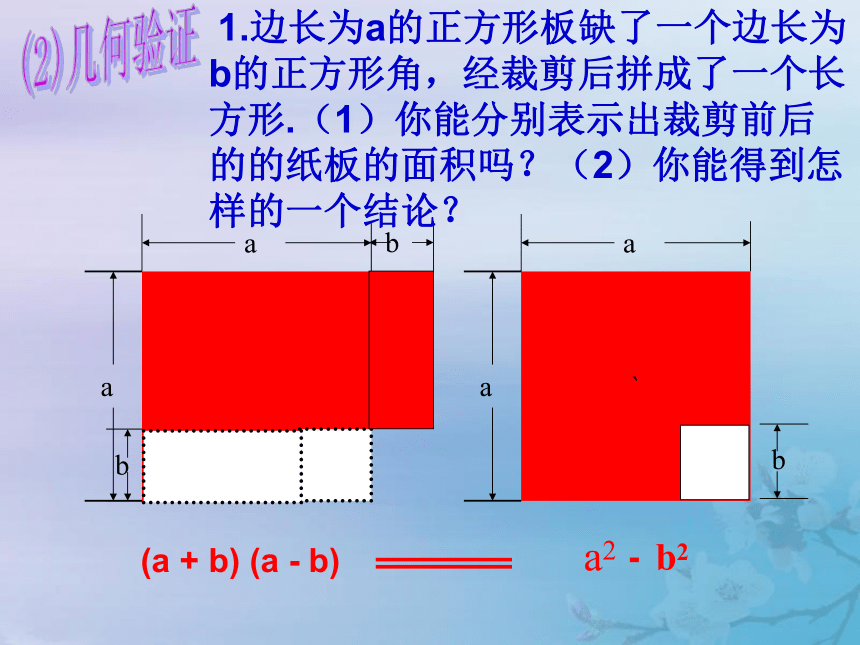
(a + b) (a - b)
1.边长为a的正方形板缺了一个边长为b的正方形角,经裁剪后拼成了一个长方形.(1)你能分别表示出裁剪前后的的纸板的面积吗?(2)你能得到怎样的一个结论?
平方差公式:
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,
等于
这两数的平方差.
(1+x)(1-x)
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
a
b
a2-b2
结果
(a+b)(a-b)
1
x
12-x2
1-x2
-3
a
(-3)2-a2
9-a2
a
1
a2-12
a2-1
0.3x
1
1、小试身手
(a+1)(a-1)
(0.3x+1)(0.3x-1)
(0.3x)2-12
0.09x2-1
快乐训练营第一站:直接运用新知,解决第一层次问题
平方差公式
(1)(a+b)(a-b)= a2 – b2
①、两个项是完全相同的,两个项是互为相反数的;
重点是观察它们的符号。
②、结果是这两数的平方差,但要注意是谁的平方减去谁的平方,符号相同数的平方减去符号不同数的平方;
(2)、(讨论)特点分析:
记忆口诀:两数和乘两数差
等于两数的平方差
2、能否运用公式,若能直接说出结果
(l)(-a+b)(a+b)=?_________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________
(5)(a+b)(-a-b)=________
(6)(a-b)(-a+b)=________
a2-b2
a2-b2
b2-a2
b2-a2
快乐训练营第二站:间接运用新知,解决第二层次问题
不能
不能
(1)(2a+b)(2b-a)=4a2-b2 ( )
(2) ( )
判断对错,并说明错误的缘由.
(3)
( )
(4) (-2x-y)(-2x+y)=4x2-y2 ( )
(5) (a+2)(a-3)=a2-6 ( )
(6) (x+3)(y-3)=xy-9 ( )
X
X
X
√
X
X
平方差公式
1、判断(是否具备公式特征)
2、调整(成标准形式)
3、计算 (注意①加括号②幂的运算)
(讨论)步骤:
例1:运用平方差公式计算:
(1)
(2)(x+2y)(x-2y)
(3) (b+2a)(2a-b)
(4) (-x+2y)(-x-2y)
(3x+2)( 3x-2 )
快乐训练营第三站:灵活运用新知,解决第三层次问题。
例2,运用平方差公式计算:
(1)10.2×9.8
(2)(x+y)(x-y)(x2+y2)
小组间每人利用平方差公式出一道题,然后交换解答,找出对方做错的地方,并通过互助共同解决问题.
1.本节课你有何收获?
2.你还有什么疑问吗?
公式:(a+b)(a-b)=a2-b2
一个
(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法
两种作用
公式中的a,b可表示
(1)单项式
(2)具体数
(3)多项式
三个表示
寄语
如果你智慧的双眼善于观察,善于发现,那你一定会觉得数学就在我们的身边。
老师相信:你辛勤的汗水一定会浇灌出智慧的花朵!
而是不断的学习.----高斯
小明同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,王捷就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你真是个神童!”王捷同学说:“过奖了,我只是利用了在数学上刚学过的一个公式.”
1计算:
⑴ (x+1)(x-1)=______ ;
⑵ (m+2)(m-2)=_____ ;
⑶ (2x+3)(2x-3)=______.
(4) (a+2b)(a-2b)=______
观察上述算式,等号左边有什么规律?
观察计算结果, 你又发现了什么规律?
- 1
- 4
- 9
2猜想:(a + b)(a- b)=——————.
a2-b2
a2-4b2
(a+b)(a-b)
3证明:(1)代数
角度
(a + b)(a- b)=a2-b2.
∴(a + b)(a- b)=a2-b2.
(多项式乘法法则)
(合并同类项)
`
a
a
b
a2
b2
-
b
a
a
b
(a + b) (a - b)
1.边长为a的正方形板缺了一个边长为b的正方形角,经裁剪后拼成了一个长方形.(1)你能分别表示出裁剪前后的的纸板的面积吗?(2)你能得到怎样的一个结论?
平方差公式:
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,
等于
这两数的平方差.
(1+x)(1-x)
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
a
b
a2-b2
结果
(a+b)(a-b)
1
x
12-x2
1-x2
-3
a
(-3)2-a2
9-a2
a
1
a2-12
a2-1
0.3x
1
1、小试身手
(a+1)(a-1)
(0.3x+1)(0.3x-1)
(0.3x)2-12
0.09x2-1
快乐训练营第一站:直接运用新知,解决第一层次问题
平方差公式
(1)(a+b)(a-b)= a2 – b2
①、两个项是完全相同的,两个项是互为相反数的;
重点是观察它们的符号。
②、结果是这两数的平方差,但要注意是谁的平方减去谁的平方,符号相同数的平方减去符号不同数的平方;
(2)、(讨论)特点分析:
记忆口诀:两数和乘两数差
等于两数的平方差
2、能否运用公式,若能直接说出结果
(l)(-a+b)(a+b)=?_________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________
(5)(a+b)(-a-b)=________
(6)(a-b)(-a+b)=________
a2-b2
a2-b2
b2-a2
b2-a2
快乐训练营第二站:间接运用新知,解决第二层次问题
不能
不能
(1)(2a+b)(2b-a)=4a2-b2 ( )
(2) ( )
判断对错,并说明错误的缘由.
(3)
( )
(4) (-2x-y)(-2x+y)=4x2-y2 ( )
(5) (a+2)(a-3)=a2-6 ( )
(6) (x+3)(y-3)=xy-9 ( )
X
X
X
√
X
X
平方差公式
1、判断(是否具备公式特征)
2、调整(成标准形式)
3、计算 (注意①加括号②幂的运算)
(讨论)步骤:
例1:运用平方差公式计算:
(1)
(2)(x+2y)(x-2y)
(3) (b+2a)(2a-b)
(4) (-x+2y)(-x-2y)
(3x+2)( 3x-2 )
快乐训练营第三站:灵活运用新知,解决第三层次问题。
例2,运用平方差公式计算:
(1)10.2×9.8
(2)(x+y)(x-y)(x2+y2)
小组间每人利用平方差公式出一道题,然后交换解答,找出对方做错的地方,并通过互助共同解决问题.
1.本节课你有何收获?
2.你还有什么疑问吗?
公式:(a+b)(a-b)=a2-b2
一个
(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法
两种作用
公式中的a,b可表示
(1)单项式
(2)具体数
(3)多项式
三个表示
寄语
如果你智慧的双眼善于观察,善于发现,那你一定会觉得数学就在我们的身边。
老师相信:你辛勤的汗水一定会浇灌出智慧的花朵!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
