苏科版七年级数学下册课件:8.2幂的乘方(共21张PPT)
文档属性
| 名称 | 苏科版七年级数学下册课件:8.2幂的乘方(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 973.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 10:44:32 | ||
图片预览







文档简介
幂的乘方
am · an
(a·a· … ·a)
n个a
=(a·a· … ·a)
m个a
= a·a· … ·a
(m+n)个a
= am+n
a·a· … ·a
an
=
am · an
=
am+n
(m , n都是正整数)
推导:
同底数幂的乘法
※2
※1
乘方的意义
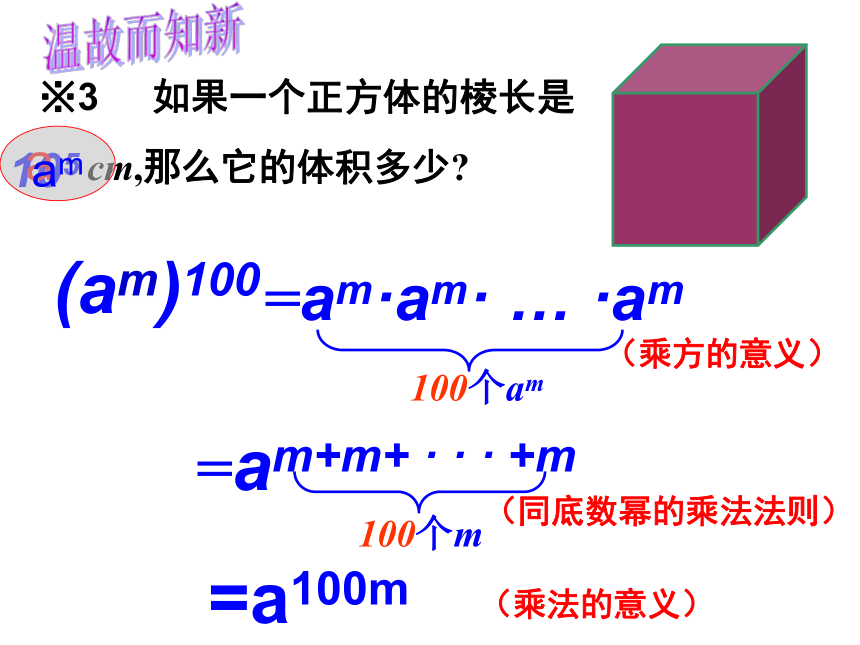
※3 如果一个正方体的棱长是
cm,那么它的体积多少?
100个m
=am+m+ · · · +m
100个am
105
a
am
=am·am· … ·am
=a100m
(am)100
(乘方的意义)
(同底数幂的乘法法则)
(乘法的意义)
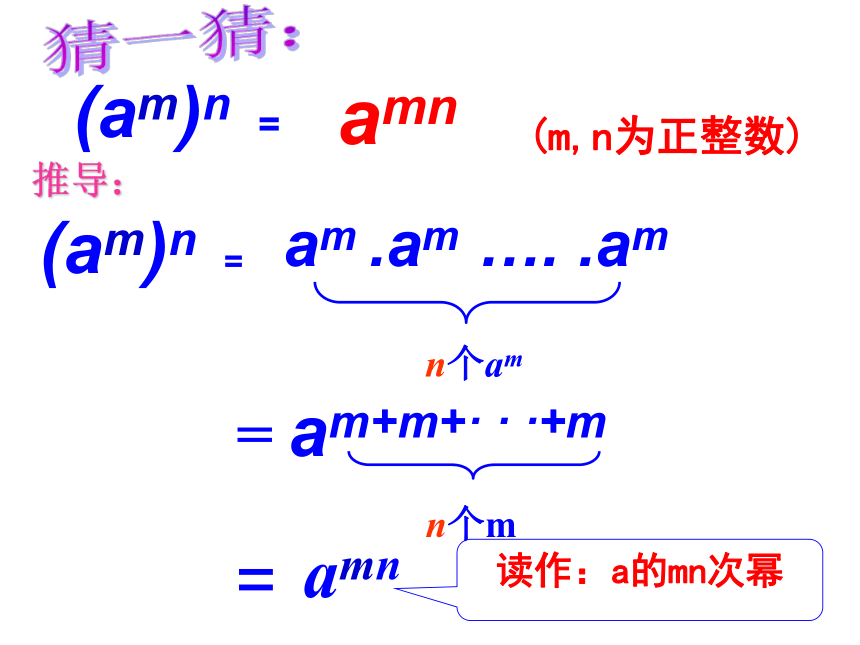
amn
n个m
= am+m+· · ·+m
n个am
am .am …. .am
=
(am)n =
读作:a的mn次幂
(am)n =
amn
(m,n为正整数)
推导:
(am)n = amn (m,n都是正整数)
底数 ,
幂的乘方,
不变
相乘
结论:
幂 的 乘 方的运算 法 则:
指数 .
用语言叙述:
【例1】计算:
幂的底数和指数不仅可以是单项式,也可以是多项式.
(am)n = amn (m,n都是正整数)
注意符号
1、判断并改正:
(a3)2 = a3+2 = a5 ( )
(2) (-a5)2 = - a10 ( )
2、直接说出结果:
×
×
a6
a10
=1020
=m10a
=x4n+8
=(x-2y) 6m
=-a10+5m
=a28
练习一:
3.有一道计算题:(-a4)2,有4种解法:
(1)(-a4)2=(-a4)(-a4)=a4a4=a8
(2)(-a4)2 = - a4×2 = - a8
(3) (-a4)2=(-a)4×2 =(-a)8= a8
(4) (-a4)2=(-1×a4)2=(-1)2(a4)2=a8
你认为其中完全正确的是(填序号)——
(1)下列各式中,与(xm+1)3相等的是( )
A. 3xm+1 B. x3m+x3
C. x3·xm+1 D. x3m·x3
D
C
4、选择:
(2). 9m·27n可以写为: ( )
A. 9m+3n B. 27m+n
C. 32m+3n D. 33m+2n
二计算:
(1) (am)3
(2) (-a2)3
(3) [(2a-b)3]2
(4) (x+y) (x+y)2[(x+y)2]3
【例2】计算:
[(am)n]p=
幂的乘方的推导
(amn)p=amnp
(m,n,p为正整数)
(am)n = amn (m,n都是正整数)
练习二:
计算
(1)a5a3+(a2)4
(2) (a3)5 (a2)2
(3) -(x3)n-xnxnxn(n是正整数)
若 (am) n=am n
=an m
=(a m)n
则 a mn
=(a n)m
例如:
x12=(x2)( ) =(x6)( )
=(x3)( ) =(x4)( )
=x7?x( ) =x?x( )
6
2
4
5
11
3
【例3】计算
1、若am=2,an=3,求① am+n 的值。
② a3m+2n的值。
2、若9×27x = 34x+1,求x的值
构建方程
逆用公式
练习三:
(1)已知22×83=2n ,求n的值.
(2)已知:2x+3y-4=0,求4x8y的值.
3、比较3555 、4444 、5333的大小.
小结与回顾
指数
底数
幂的乘方
同底数幂乘法
计算结果
法则
中运算
公式
运算
种类
乘法
乘方
不变
不变
指数
相加
指数
相乘
进 步 的 阶 梯(1)
下列计算是否正确,如有错误,请改正.
⑴ (a5)2=a7;
⑵ a5·a2=a10;
⑶ (-a3)3=a9;
⑷ a7+a3=a10;
⑸ (xn+1)2=x2n+1(n是正整数);
⑹ (-x2)2n=x4n (n是正整数).
√
(a5)2=a10
a5·a2=a7
(-a3)3=-a9
无法计算
(xn+1)2=x2n+2
1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.
3、若(-2)2 · 24= (a3)2,则a=______
8
6
72
±2
在255,344,433,522,这四个幂的数值中,最大的一个是_______
344
1.比较230与320的大小
2.比较2100与375的大小.
1.若am=3,an=2,求a2m+3n的值.(A本)
2.已知,44?83=2x,求x的值. (A本)
B本
1. 已知a3n=5,b2n=3,求:a6nb4n的值.
2. 设n为正整数,且x2n=2,求9(x3n)2的值.
3. 已知2m=a,32n=b,求:23m+10n.
am · an
(a·a· … ·a)
n个a
=(a·a· … ·a)
m个a
= a·a· … ·a
(m+n)个a
= am+n
a·a· … ·a
an
=
am · an
=
am+n
(m , n都是正整数)
推导:
同底数幂的乘法
※2
※1
乘方的意义
※3 如果一个正方体的棱长是
cm,那么它的体积多少?
100个m
=am+m+ · · · +m
100个am
105
a
am
=am·am· … ·am
=a100m
(am)100
(乘方的意义)
(同底数幂的乘法法则)
(乘法的意义)
amn
n个m
= am+m+· · ·+m
n个am
am .am …. .am
=
(am)n =
读作:a的mn次幂
(am)n =
amn
(m,n为正整数)
推导:
(am)n = amn (m,n都是正整数)
底数 ,
幂的乘方,
不变
相乘
结论:
幂 的 乘 方的运算 法 则:
指数 .
用语言叙述:
【例1】计算:
幂的底数和指数不仅可以是单项式,也可以是多项式.
(am)n = amn (m,n都是正整数)
注意符号
1、判断并改正:
(a3)2 = a3+2 = a5 ( )
(2) (-a5)2 = - a10 ( )
2、直接说出结果:
×
×
a6
a10
=1020
=m10a
=x4n+8
=(x-2y) 6m
=-a10+5m
=a28
练习一:
3.有一道计算题:(-a4)2,有4种解法:
(1)(-a4)2=(-a4)(-a4)=a4a4=a8
(2)(-a4)2 = - a4×2 = - a8
(3) (-a4)2=(-a)4×2 =(-a)8= a8
(4) (-a4)2=(-1×a4)2=(-1)2(a4)2=a8
你认为其中完全正确的是(填序号)——
(1)下列各式中,与(xm+1)3相等的是( )
A. 3xm+1 B. x3m+x3
C. x3·xm+1 D. x3m·x3
D
C
4、选择:
(2). 9m·27n可以写为: ( )
A. 9m+3n B. 27m+n
C. 32m+3n D. 33m+2n
二计算:
(1) (am)3
(2) (-a2)3
(3) [(2a-b)3]2
(4) (x+y) (x+y)2[(x+y)2]3
【例2】计算:
[(am)n]p=
幂的乘方的推导
(amn)p=amnp
(m,n,p为正整数)
(am)n = amn (m,n都是正整数)
练习二:
计算
(1)a5a3+(a2)4
(2) (a3)5 (a2)2
(3) -(x3)n-xnxnxn(n是正整数)
若 (am) n=am n
=an m
=(a m)n
则 a mn
=(a n)m
例如:
x12=(x2)( ) =(x6)( )
=(x3)( ) =(x4)( )
=x7?x( ) =x?x( )
6
2
4
5
11
3
【例3】计算
1、若am=2,an=3,求① am+n 的值。
② a3m+2n的值。
2、若9×27x = 34x+1,求x的值
构建方程
逆用公式
练习三:
(1)已知22×83=2n ,求n的值.
(2)已知:2x+3y-4=0,求4x8y的值.
3、比较3555 、4444 、5333的大小.
小结与回顾
指数
底数
幂的乘方
同底数幂乘法
计算结果
法则
中运算
公式
运算
种类
乘法
乘方
不变
不变
指数
相加
指数
相乘
进 步 的 阶 梯(1)
下列计算是否正确,如有错误,请改正.
⑴ (a5)2=a7;
⑵ a5·a2=a10;
⑶ (-a3)3=a9;
⑷ a7+a3=a10;
⑸ (xn+1)2=x2n+1(n是正整数);
⑹ (-x2)2n=x4n (n是正整数).
√
(a5)2=a10
a5·a2=a7
(-a3)3=-a9
无法计算
(xn+1)2=x2n+2
1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.
3、若(-2)2 · 24= (a3)2,则a=______
8
6
72
±2
在255,344,433,522,这四个幂的数值中,最大的一个是_______
344
1.比较230与320的大小
2.比较2100与375的大小.
1.若am=3,an=2,求a2m+3n的值.(A本)
2.已知,44?83=2x,求x的值. (A本)
B本
1. 已知a3n=5,b2n=3,求:a6nb4n的值.
2. 设n为正整数,且x2n=2,求9(x3n)2的值.
3. 已知2m=a,32n=b,求:23m+10n.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
