苏科版七年级数学下册课件:10.3复习二元一次方程组的解法(共15张PPT)
文档属性
| 名称 | 苏科版七年级数学下册课件:10.3复习二元一次方程组的解法(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 280.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 10:48:36 | ||
图片预览



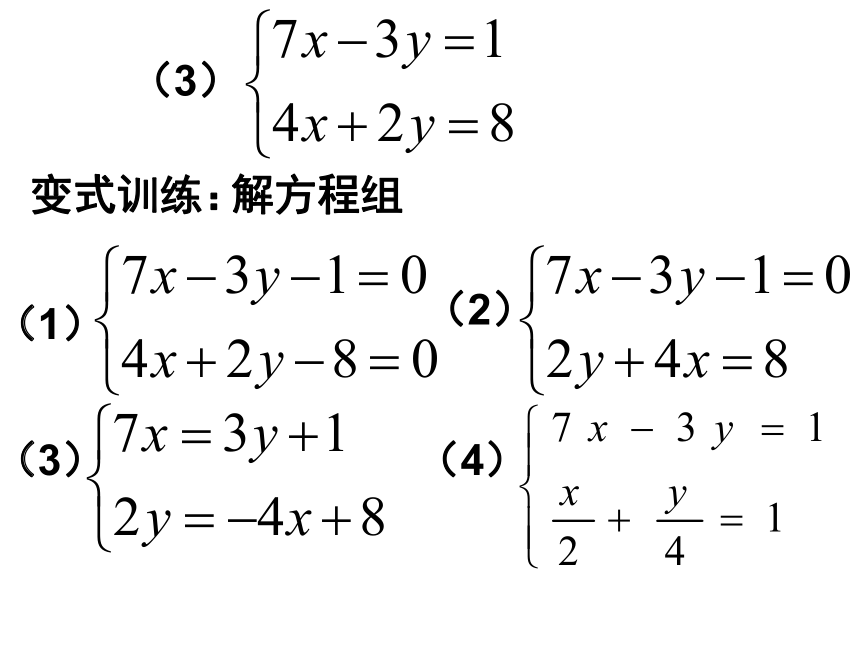

文档简介
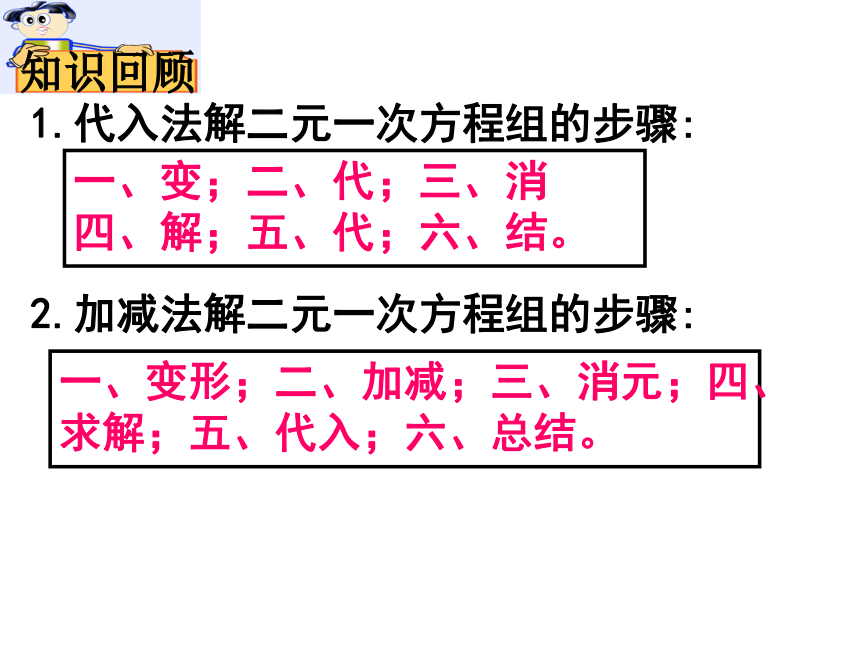
1.代入法解二元一次方程组的步骤:
一、变;二、代;三、消 四、解;五、代;六、结。
2.加减法解二元一次方程组的步骤:
一、变形;二、加减;三、消元;四、求解;五、代入;六、总结。
例1.用代入法和加减法解方程组:
例2.选择适当方法解方程组:
(1)
(2)
(3)
变式训练:
(3)
解方程组
(1)
(2)
(3)
(4)
例3.解方程组:
(1)
(2)
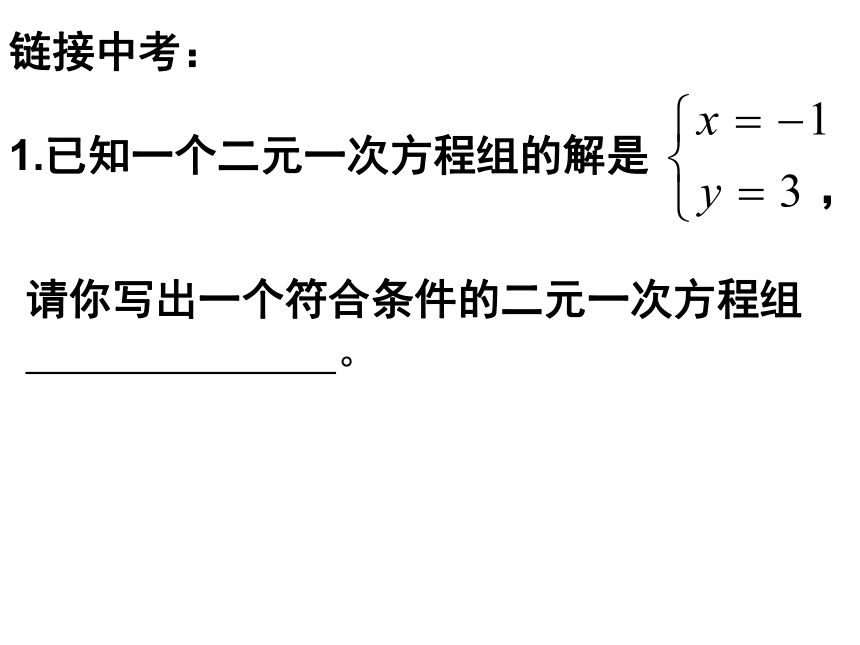
链接中考:
1.已知一个二元一次方程组的解是
,
请你写出一个符合条件的二元一次方程组
。
2.阅读:解方程组
①
②
由
①得,x-y=1
③
把
③代入
②得,4x1-y=5,
解之得,y=-1
把y=-1代入 ,解得 x=0
①
∴原方程组的解为
求解:请用上面的方法解方程组
拓展提升:
1.已知关于x、y的方程组
与 有相同的解,求出这个解
及a、b的值。
①
②
③
④
拓展提升:
2.甲、乙两人同时解方程组
甲看错了①中的m,解得
,乙看错
了②中的n,解得
确值.
,试求m、n的正
①
②
已知关于x、y的方程组 与
的解相同,求a、b
的值.
ax+2by=4①
x+y=1②
x-y=3③
bx+(a-1)y=3④
已知关于x、y的方程组的解
满足x+y=4,求a的值.
3x+2y=a+2
2x+3y=2a
相信你能行
1.
2.
拓展提高
1.解方程组
2.已知二元一次方程 的两
个解为 和 ,
求 的值。
课堂小结
2.加减法的基本思想:消元。
3.加减法解二元一次方程组主要步骤:
1.加减消元法
将方程组的两个方程(或先作适当变形)相加或相减,消去一个未知数,把解二元一次方程组转化为解一元一次方程。这种解方程组的方法称为加减消元法,简称为加减法。
一加减,二消元,三求解,四代入,五总结
例3:解方程组
练一练
⑴
0.6x-0.5y=0.4
2X-3y=4
(2)
3X-4y=-7
(3)
X-2y=-1
练一练:解下列方程组
(1)
(2)
一、变;二、代;三、消 四、解;五、代;六、结。
2.加减法解二元一次方程组的步骤:
一、变形;二、加减;三、消元;四、求解;五、代入;六、总结。
例1.用代入法和加减法解方程组:
例2.选择适当方法解方程组:
(1)
(2)
(3)
变式训练:
(3)
解方程组
(1)
(2)
(3)
(4)
例3.解方程组:
(1)
(2)
链接中考:
1.已知一个二元一次方程组的解是
,
请你写出一个符合条件的二元一次方程组
。
2.阅读:解方程组
①
②
由
①得,x-y=1
③
把
③代入
②得,4x1-y=5,
解之得,y=-1
把y=-1代入 ,解得 x=0
①
∴原方程组的解为
求解:请用上面的方法解方程组
拓展提升:
1.已知关于x、y的方程组
与 有相同的解,求出这个解
及a、b的值。
①
②
③
④
拓展提升:
2.甲、乙两人同时解方程组
甲看错了①中的m,解得
,乙看错
了②中的n,解得
确值.
,试求m、n的正
①
②
已知关于x、y的方程组 与
的解相同,求a、b
的值.
ax+2by=4①
x+y=1②
x-y=3③
bx+(a-1)y=3④
已知关于x、y的方程组的解
满足x+y=4,求a的值.
3x+2y=a+2
2x+3y=2a
相信你能行
1.
2.
拓展提高
1.解方程组
2.已知二元一次方程 的两
个解为 和 ,
求 的值。
课堂小结
2.加减法的基本思想:消元。
3.加减法解二元一次方程组主要步骤:
1.加减消元法
将方程组的两个方程(或先作适当变形)相加或相减,消去一个未知数,把解二元一次方程组转化为解一元一次方程。这种解方程组的方法称为加减消元法,简称为加减法。
一加减,二消元,三求解,四代入,五总结
例3:解方程组
练一练
⑴
0.6x-0.5y=0.4
2X-3y=4
(2)
3X-4y=-7
(3)
X-2y=-1
练一练:解下列方程组
(1)
(2)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
