苏科版七年级数学下册课件:第7章 平面图形的认识(复习)小结与思考(共25张PPT)
文档属性
| 名称 | 苏科版七年级数学下册课件:第7章 平面图形的认识(复习)小结与思考(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 653.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 10:49:51 | ||
图片预览






文档简介
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
平面图形的认识(复习)
在两条被截线的, 在截线
的 ,这样的一对角称为同位角
在两条被截线 ,在截线的
这样的一对角称为内错角.
在两条被截线 ,在截线的 ,
这样的一对角称为同旁内角.
同位角
内错角
同旁内角
1
3
5
7
2
4
6
8
a
b
c
同一方向
同旁
之间
之间
同旁
两旁
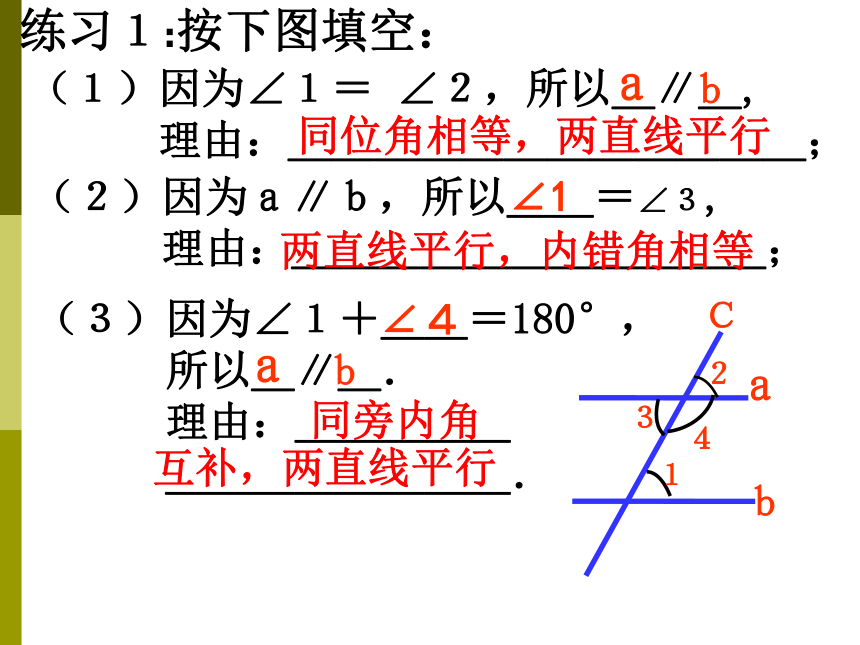
1.如图,∠1与∠B,∠3与∠4,∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?
1
2
3
4
A
B
C
D
练一练
E
知识点梳理
一、两
同旁内角互补,两直线平行.
内错角相等,两直线平行.
同位角相等,两直线平行.
两直线平行,同旁内角互补.
两直线平行,同位角相等.
两直线平行,内错角相等.
直线平行的条件:
二、两
直线
平行的性质:
两条平行直线被第三条直线直线所截,
同位角相等, 两直线平行
两直线平行,同位角相等。
判定(数----形)
性质(形----数)
条件 结论
条件 结论
思考:
1、判定定理与性质定理的
条件与结论有什么关系?
互换。
内错角相等, 两直线平行
两直线平行,内错角相等。
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2、使用判定定理时是
已知 ,说明 ;
角的关系
两直线平行
使用性质定理时是
已知 ,说明 。
两直线平行
角的关系
练习1:按下图填空:
(2)因为a∥b,所以__=∠3,
理由:___________;
(3)因为∠1+__=180°,
所以_∥_.
理由:_____
________.
(1)因为∠1= ∠2,所以_∥_,
理由:____________;
a
b
C
1
2
3
4
a
b
同位角相等,两直线平行
两直线平行,内错角相等
a
b
同旁内角
互补,两直线平行
∠1
∠4
(1)因为∠1=∠2,所以__∥__,
理由是______,两直线平行.
A
B
C
D
1
2
3
4
AB CD
内错角相等
(2)因为AD∥BC,所以
∠D+_____=180°理由
是__________
___________.
两直线平行,
同旁内角互补
∠BCD
练习2:按图填空:
A
B
D
E
F
1
2
3
4
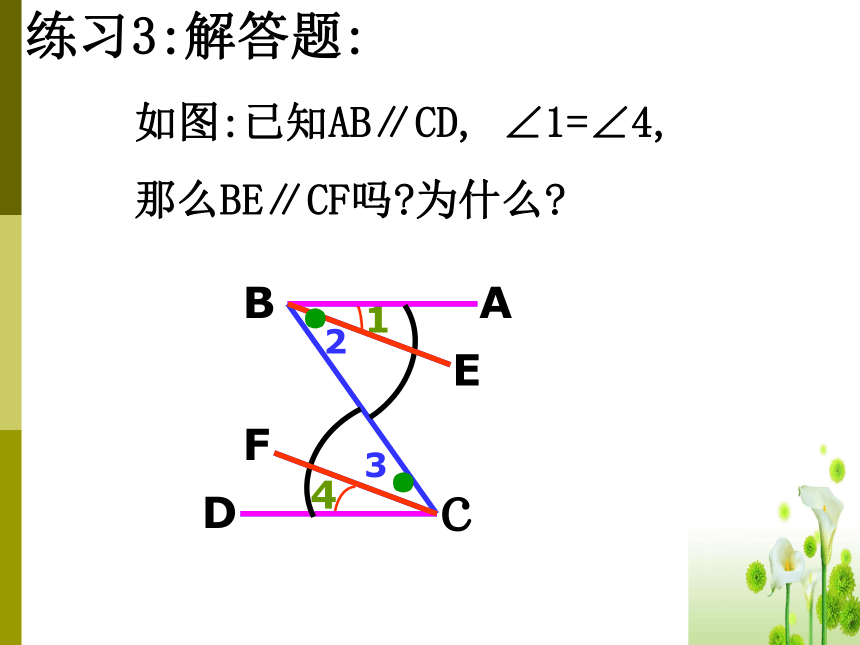
如图:已知AB∥CD, ∠1=∠4,
那么BE∥CF吗?为什么?
练习3:解答题:
c
·
·
平移的概念:
三、平移的概念及特征:
在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移
平移不改变图形的____和_____.
平移的特征:
形状
大小
图形经过平移,连接各组对应点的线段平行且相等或在同一条直线上且相等.
四.平移的性质:
练习4:计算:
(1)如图,大矩形的长是10cm,宽是8cm,阴影部分的宽为2cm,则空白部分的面积是多少?
②若∠BAE=60°,∠AEB=98°,则∠DcF= °,∠CFD= °.
(2)如图,△ABE向右平移一定距离后
得到△CDF.
①图中存在平行且相等的三组线段是
AB和 ,AE和 ,AC和 .
CD
CF
BD或EF
60°
98°
60
98
D
E
B
A
C
F
五、三角形的有关知识结构:
①三角形3个内角的和等于______.
180°
②直角三角形的两个锐角____.
互余
③三角形的一个外角等于_____
____________.
相邻的两个内角的和
与它不
④三角形的两边之和___第三边.
大于
⑤三角形的角平分线、中线、高线分别有几条?它们是如何分布的?
它们的交点情况又如何呢?
六.多边形的有关知识结构:
①n边形的内角和等于_____________.
(n-2) ×180°
②n边形的外角和等于______.
360°
练习5: (1)按图填空:
②∠ A+ ∠B+ ∠ACB=_____;
①AB+AC__BC(填“﹥”、“<”或“=”)
A
B
C
D
③ ∠ACD= ∠___+ ∠___
﹥
180°
A B
(2)有长为3、5、7、10的四根木条,从中
选三根能摆出( )个三角形
A 、1 B、2 C、3 D、4
B
(3)在△ABC中,AB=7 BC=3,并且AC
为偶数,那么△ABC的周长为_____.
16或18
(4)如果一个多边形的每个内角都相等,且每
个内角都比与它相邻的外角大60°,求
这个多边形的边数及每个内角的度数.
(5)在△ABC中, ∠A+∠B=110°,
∠C=2∠B,求 ∠A、∠B、∠ C的度数.
(6)如图:已知∠CAD=∠CDA,∠1=∠B,
试说明AD平分∠BAE.
A
B
C
D
E
1
·
·
2
3
(7)在△ABC中,设n为线段BC上新增加点的个
数,s为连结A与新增点所得三角形的总个数.
①填表:
新增加点的个数n
所得三角形的总数s
0
1
2
3
…
C
A
B
A
B
C
A
B
C
1
3
6
10
C
A
B
…
新增加点的个数n
所得三角形的总数s
0
1
2
3
…
1
3
6
10
…
②设新增加m个点后三角形的总个数为P,则新增加m+1个点后三角形的总个数为_______.
P+m+2
③新增加n个点可得 三角形.
我要说…
2.我从同伴身上学到了什么?
1.这节课我学到了什么?
多边形相关的知识点:
多边形的对角线:连接多边形不相邻的 两个顶点的线段,叫做多边形的对角线.
如图,AC、AD是五边形ABCDE的对角线
A
B
C
D
E
你能解决吗?
四边形ABCD中,过顶点A可以画___条对角线
五边形ABCDE中,过顶点A可以画___条对角线
六边形ABCDEF中,过顶点A可以画___条对角线
观察并回答:
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
由上图可知:
A2
A1
A3
A4
A5
A6
An
相信你能行!
(1)如图,n边形中,过顶点A1可以画___条对角线,它们分别是:_________;过顶点A2可以画____条对角线;过顶点A3可以画___条对角线.
(2)过顶点A1的对角线与过顶点A2的对角线有相同的吗?过顶点A1的对角线与过顶点A3的对角线有相同的吗?
(3)在此基础上,你能发现n边形的对角线条数的规律吗?
5.如图:已知AC平分∠BAD, ∠1=∠2,∠B=70°. (1)试说明AB ∥ CD; (2)求 ∠BCD的度数
A
B
C
D
2
3
1
6.如图:已知AB∥CD, ∠1=∠4,试说明BE∥CF
7.在△ABC中,∠A+∠B=110°,∠C=2∠B,求∠A、∠B、∠C的度数.
图5
A
B
C
D
E
F
1
2
3
4
图6
5.如图:已知AC平分∠BAD, ∠1=∠2,∠B=70°. (1)试说明AB ∥ CD; (2)求 ∠BCD的度数
1. 如图:∠A的同位角是_____, ∠3的内错角是_____, ∠A的同旁内角是__________, ∠C的同位角是____.
2.如图:若∠C=___,则DE∥BC.理由____
若∠2+_=180°,则_∥_.理由______
若_=∠B,则EF∥_.理由________
若∠2=∠4,则_∥_.理由________
A
B
C
D
E
1
2
3
4
图1
知识点应用
A
B
C
D
E
F
1
2
3
4
图2
3.如图,若AB∥CD,CD∥EF, 则AB与EF的位置关系是_______.
4.如图:若AB⊥CD,CD∥EF,则AB与EF 的位置关系是_______.
A
B
C
D
E
F
1
图3
A
B
C
D
E
F
图4
A
B
C
8.画出△ABC沿如图所示方向平移4㎝后的图形.
单击此处编辑母版副标题样式
*
*
*
平面图形的认识(复习)
在两条被截线的, 在截线
的 ,这样的一对角称为同位角
在两条被截线 ,在截线的
这样的一对角称为内错角.
在两条被截线 ,在截线的 ,
这样的一对角称为同旁内角.
同位角
内错角
同旁内角
1
3
5
7
2
4
6
8
a
b
c
同一方向
同旁
之间
之间
同旁
两旁
1.如图,∠1与∠B,∠3与∠4,∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?
1
2
3
4
A
B
C
D
练一练
E
知识点梳理
一、两
同旁内角互补,两直线平行.
内错角相等,两直线平行.
同位角相等,两直线平行.
两直线平行,同旁内角互补.
两直线平行,同位角相等.
两直线平行,内错角相等.
直线平行的条件:
二、两
直线
平行的性质:
两条平行直线被第三条直线直线所截,
同位角相等, 两直线平行
两直线平行,同位角相等。
判定(数----形)
性质(形----数)
条件 结论
条件 结论
思考:
1、判定定理与性质定理的
条件与结论有什么关系?
互换。
内错角相等, 两直线平行
两直线平行,内错角相等。
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2、使用判定定理时是
已知 ,说明 ;
角的关系
两直线平行
使用性质定理时是
已知 ,说明 。
两直线平行
角的关系
练习1:按下图填空:
(2)因为a∥b,所以__=∠3,
理由:___________;
(3)因为∠1+__=180°,
所以_∥_.
理由:_____
________.
(1)因为∠1= ∠2,所以_∥_,
理由:____________;
a
b
C
1
2
3
4
a
b
同位角相等,两直线平行
两直线平行,内错角相等
a
b
同旁内角
互补,两直线平行
∠1
∠4
(1)因为∠1=∠2,所以__∥__,
理由是______,两直线平行.
A
B
C
D
1
2
3
4
AB CD
内错角相等
(2)因为AD∥BC,所以
∠D+_____=180°理由
是__________
___________.
两直线平行,
同旁内角互补
∠BCD
练习2:按图填空:
A
B
D
E
F
1
2
3
4
如图:已知AB∥CD, ∠1=∠4,
那么BE∥CF吗?为什么?
练习3:解答题:
c
·
·
平移的概念:
三、平移的概念及特征:
在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移
平移不改变图形的____和_____.
平移的特征:
形状
大小
图形经过平移,连接各组对应点的线段平行且相等或在同一条直线上且相等.
四.平移的性质:
练习4:计算:
(1)如图,大矩形的长是10cm,宽是8cm,阴影部分的宽为2cm,则空白部分的面积是多少?
②若∠BAE=60°,∠AEB=98°,则∠DcF= °,∠CFD= °.
(2)如图,△ABE向右平移一定距离后
得到△CDF.
①图中存在平行且相等的三组线段是
AB和 ,AE和 ,AC和 .
CD
CF
BD或EF
60°
98°
60
98
D
E
B
A
C
F
五、三角形的有关知识结构:
①三角形3个内角的和等于______.
180°
②直角三角形的两个锐角____.
互余
③三角形的一个外角等于_____
____________.
相邻的两个内角的和
与它不
④三角形的两边之和___第三边.
大于
⑤三角形的角平分线、中线、高线分别有几条?它们是如何分布的?
它们的交点情况又如何呢?
六.多边形的有关知识结构:
①n边形的内角和等于_____________.
(n-2) ×180°
②n边形的外角和等于______.
360°
练习5: (1)按图填空:
②∠ A+ ∠B+ ∠ACB=_____;
①AB+AC__BC(填“﹥”、“<”或“=”)
A
B
C
D
③ ∠ACD= ∠___+ ∠___
﹥
180°
A B
(2)有长为3、5、7、10的四根木条,从中
选三根能摆出( )个三角形
A 、1 B、2 C、3 D、4
B
(3)在△ABC中,AB=7 BC=3,并且AC
为偶数,那么△ABC的周长为_____.
16或18
(4)如果一个多边形的每个内角都相等,且每
个内角都比与它相邻的外角大60°,求
这个多边形的边数及每个内角的度数.
(5)在△ABC中, ∠A+∠B=110°,
∠C=2∠B,求 ∠A、∠B、∠ C的度数.
(6)如图:已知∠CAD=∠CDA,∠1=∠B,
试说明AD平分∠BAE.
A
B
C
D
E
1
·
·
2
3
(7)在△ABC中,设n为线段BC上新增加点的个
数,s为连结A与新增点所得三角形的总个数.
①填表:
新增加点的个数n
所得三角形的总数s
0
1
2
3
…
C
A
B
A
B
C
A
B
C
1
3
6
10
C
A
B
…
新增加点的个数n
所得三角形的总数s
0
1
2
3
…
1
3
6
10
…
②设新增加m个点后三角形的总个数为P,则新增加m+1个点后三角形的总个数为_______.
P+m+2
③新增加n个点可得 三角形.
我要说…
2.我从同伴身上学到了什么?
1.这节课我学到了什么?
多边形相关的知识点:
多边形的对角线:连接多边形不相邻的 两个顶点的线段,叫做多边形的对角线.
如图,AC、AD是五边形ABCDE的对角线
A
B
C
D
E
你能解决吗?
四边形ABCD中,过顶点A可以画___条对角线
五边形ABCDE中,过顶点A可以画___条对角线
六边形ABCDEF中,过顶点A可以画___条对角线
观察并回答:
A
B
C
D
A
B
C
D
E
A
B
C
D
E
F
由上图可知:
A2
A1
A3
A4
A5
A6
An
相信你能行!
(1)如图,n边形中,过顶点A1可以画___条对角线,它们分别是:_________;过顶点A2可以画____条对角线;过顶点A3可以画___条对角线.
(2)过顶点A1的对角线与过顶点A2的对角线有相同的吗?过顶点A1的对角线与过顶点A3的对角线有相同的吗?
(3)在此基础上,你能发现n边形的对角线条数的规律吗?
5.如图:已知AC平分∠BAD, ∠1=∠2,∠B=70°. (1)试说明AB ∥ CD; (2)求 ∠BCD的度数
A
B
C
D
2
3
1
6.如图:已知AB∥CD, ∠1=∠4,试说明BE∥CF
7.在△ABC中,∠A+∠B=110°,∠C=2∠B,求∠A、∠B、∠C的度数.
图5
A
B
C
D
E
F
1
2
3
4
图6
5.如图:已知AC平分∠BAD, ∠1=∠2,∠B=70°. (1)试说明AB ∥ CD; (2)求 ∠BCD的度数
1. 如图:∠A的同位角是_____, ∠3的内错角是_____, ∠A的同旁内角是__________, ∠C的同位角是____.
2.如图:若∠C=___,则DE∥BC.理由____
若∠2+_=180°,则_∥_.理由______
若_=∠B,则EF∥_.理由________
若∠2=∠4,则_∥_.理由________
A
B
C
D
E
1
2
3
4
图1
知识点应用
A
B
C
D
E
F
1
2
3
4
图2
3.如图,若AB∥CD,CD∥EF, 则AB与EF的位置关系是_______.
4.如图:若AB⊥CD,CD∥EF,则AB与EF 的位置关系是_______.
A
B
C
D
E
F
1
图3
A
B
C
D
E
F
图4
A
B
C
8.画出△ABC沿如图所示方向平移4㎝后的图形.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
