苏科版七年级下册 8.1 同底数幂的乘法 课件(共18张PPT)
文档属性
| 名称 | 苏科版七年级下册 8.1 同底数幂的乘法 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览






文档简介
8.1 同底数幂的乘法
七年级(下册)
初中数学
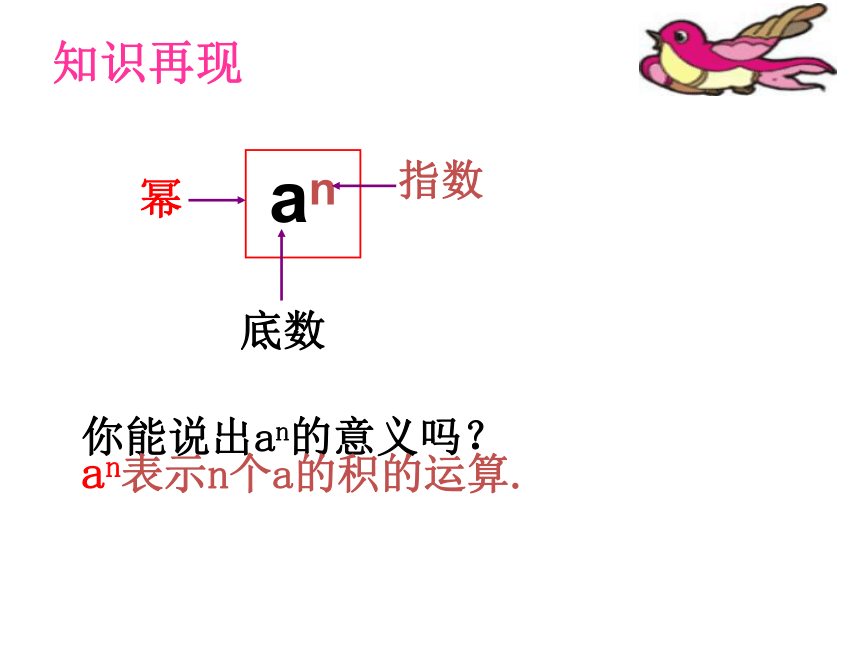
an
底数
指数
幂
知识再现
你能说出an的意义吗?
an表示n个a的积的运算.
填空:
1.2×2×2×2=2( )
2.10×10×10×…×10=10( )
3.a×a×a×a×a×a=a( )
4.a×a×a×…×a=a( )
5.(-1)2m=__,(-1)2m+1=__.(m是正整数)
7个10
n个a
4
7
6
n
练一练
1
-1
太阳光照射到地球表面所需的时间约是 秒,光的速度约是 米/秒,地球与太阳之间的距离约是多少?
数的世界充满着神奇,幂的运算方便了对 数的处理!
大
(3×108)×(5×102)
=(3×5)×(108×102)
108×102等于多少呢?
试一试
33×32=(3×3×3) ×(3×3)
表示5个3相乘
=35
计算:33×32
请观察运算前后,底数和指数的关系,你发现了什么?
(m、n是正整数)
(a×a×a×…×a)·(a×a×a×…×a)
规律探究
用m、n表示a的指数,m、n是正整数,则am·an的结果是多少呢?
am·an=
m个a
n个a
=a×a×a×…×a
(m+n)个a
=am+n
结论
am·an=am+n(m、n都是正整数)
结论
am·an=am+n(m、n都是正整数)
结论
am·an=am+n(m、n都是正整数)
你能用文字语言将同底数幂乘法的性质叙述出来吗?
同底数幂相乘,底数 ,指数 .
请你推广:
am·an·ap=
am+n+p
(m、n、p都是正整数)
运用同底数幂的乘法性质的条件:
1、判断是同底数幂
2、是乘法
不变
相加
am·an·ap=
am+n+p
(m、n、p都是正整数)
8.1 同底数幂的乘法
例1.计算
(1)
指数是“1”
( 是正整数)
(4)
(3)
(2)
太阳光照射到地球表面所需的时间约是 秒,光的速度约是 米/秒,地球与太阳之间的距离约是多少?
解:(3×108)×(5×102)
=(3×5)×(108×102)
=15×1010
=1.5×1011(m)
答:地球与太阳之间的距离约是1.5×1011m.
5
2n
(1)a7·a(__)=a12;
(2)an·a(___) = a3n;
(3)若3×27×35 = 3x,则 x= ___.
填空:
33
9
3× ×35 =
39
8.1 同底数幂的乘法
例2.一颗卫星绕地球运行的速度
是 ,求这颗卫星运行1h的路程.
a3·a( )=a8;
(2)a4·_____·a2=a10;
(3)若a4·am=a10,则m=____;
(4)若xm·xm=x8,则m=____;
(5)若x·xa·x4=x2a+3,则a=____.
5
a4
6
4
2
试一试:
已知am=8,an=32,求am+n的值.
巩固练习
巩固练习
下列计算是否正确?
(1)a2+a3=2a5 ( ) (2)a2·a3=a5 ( )
(3)a2·a3=a6 ( ) (4)a2+a3=a5 ( )
(5)a2+a2=a4 ( ) (6)xm+xm=2xm ( )
(7)25 + 25=210 ( ) (8)25 + 25=26 ( )
×
×
×
×
√
×
√
√
例3.计算
x2·x5+x3·x4
练习:计算
1.y4·y-y·y·y3;
2.2×24+22×23;
3.a2·a·a5+a3·a2·a3.
例题分析
1.计算:
(1) a7·(-a)6; (2)(x+y)3·(-x-y)2.
2.一个长方体的长为4×103厘米,宽为2×102厘米,高为2.5×103厘米,则它的体积为( )立方厘米
(结果用科学记数法表示) .
A.2×109 B.20×108 C.20×1018 D.8.5×108
3.已知xm = 3,xn = 5,求xm+n.
8.1 同底数幂的乘法
4.计算:
(1)(x-y)·(y-x)2· (x-y)5;
(2)an·an+1+a2n·a(n是正整数).
8.1 同底数幂的乘法
通过这节课的学习:
我最大的收获是______________
我对自己的表现评价如何_____________
我从同学身上学到了________________
总
结
与
回
顾
七年级(下册)
初中数学
an
底数
指数
幂
知识再现
你能说出an的意义吗?
an表示n个a的积的运算.
填空:
1.2×2×2×2=2( )
2.10×10×10×…×10=10( )
3.a×a×a×a×a×a=a( )
4.a×a×a×…×a=a( )
5.(-1)2m=__,(-1)2m+1=__.(m是正整数)
7个10
n个a
4
7
6
n
练一练
1
-1
太阳光照射到地球表面所需的时间约是 秒,光的速度约是 米/秒,地球与太阳之间的距离约是多少?
数的世界充满着神奇,幂的运算方便了对 数的处理!
大
(3×108)×(5×102)
=(3×5)×(108×102)
108×102等于多少呢?
试一试
33×32=(3×3×3) ×(3×3)
表示5个3相乘
=35
计算:33×32
请观察运算前后,底数和指数的关系,你发现了什么?
(m、n是正整数)
(a×a×a×…×a)·(a×a×a×…×a)
规律探究
用m、n表示a的指数,m、n是正整数,则am·an的结果是多少呢?
am·an=
m个a
n个a
=a×a×a×…×a
(m+n)个a
=am+n
结论
am·an=am+n(m、n都是正整数)
结论
am·an=am+n(m、n都是正整数)
结论
am·an=am+n(m、n都是正整数)
你能用文字语言将同底数幂乘法的性质叙述出来吗?
同底数幂相乘,底数 ,指数 .
请你推广:
am·an·ap=
am+n+p
(m、n、p都是正整数)
运用同底数幂的乘法性质的条件:
1、判断是同底数幂
2、是乘法
不变
相加
am·an·ap=
am+n+p
(m、n、p都是正整数)
8.1 同底数幂的乘法
例1.计算
(1)
指数是“1”
( 是正整数)
(4)
(3)
(2)
太阳光照射到地球表面所需的时间约是 秒,光的速度约是 米/秒,地球与太阳之间的距离约是多少?
解:(3×108)×(5×102)
=(3×5)×(108×102)
=15×1010
=1.5×1011(m)
答:地球与太阳之间的距离约是1.5×1011m.
5
2n
(1)a7·a(__)=a12;
(2)an·a(___) = a3n;
(3)若3×27×35 = 3x,则 x= ___.
填空:
33
9
3× ×35 =
39
8.1 同底数幂的乘法
例2.一颗卫星绕地球运行的速度
是 ,求这颗卫星运行1h的路程.
a3·a( )=a8;
(2)a4·_____·a2=a10;
(3)若a4·am=a10,则m=____;
(4)若xm·xm=x8,则m=____;
(5)若x·xa·x4=x2a+3,则a=____.
5
a4
6
4
2
试一试:
已知am=8,an=32,求am+n的值.
巩固练习
巩固练习
下列计算是否正确?
(1)a2+a3=2a5 ( ) (2)a2·a3=a5 ( )
(3)a2·a3=a6 ( ) (4)a2+a3=a5 ( )
(5)a2+a2=a4 ( ) (6)xm+xm=2xm ( )
(7)25 + 25=210 ( ) (8)25 + 25=26 ( )
×
×
×
×
√
×
√
√
例3.计算
x2·x5+x3·x4
练习:计算
1.y4·y-y·y·y3;
2.2×24+22×23;
3.a2·a·a5+a3·a2·a3.
例题分析
1.计算:
(1) a7·(-a)6; (2)(x+y)3·(-x-y)2.
2.一个长方体的长为4×103厘米,宽为2×102厘米,高为2.5×103厘米,则它的体积为( )立方厘米
(结果用科学记数法表示) .
A.2×109 B.20×108 C.20×1018 D.8.5×108
3.已知xm = 3,xn = 5,求xm+n.
8.1 同底数幂的乘法
4.计算:
(1)(x-y)·(y-x)2· (x-y)5;
(2)an·an+1+a2n·a(n是正整数).
8.1 同底数幂的乘法
通过这节课的学习:
我最大的收获是______________
我对自己的表现评价如何_____________
我从同学身上学到了________________
总
结
与
回
顾
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
