苏科版七年级下册数学 8.2《幂的运算 》 课件 (共26张PPT)
文档属性
| 名称 | 苏科版七年级下册数学 8.2《幂的运算 》 课件 (共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 473.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 10:52:18 | ||
图片预览







文档简介
幂的运算
am
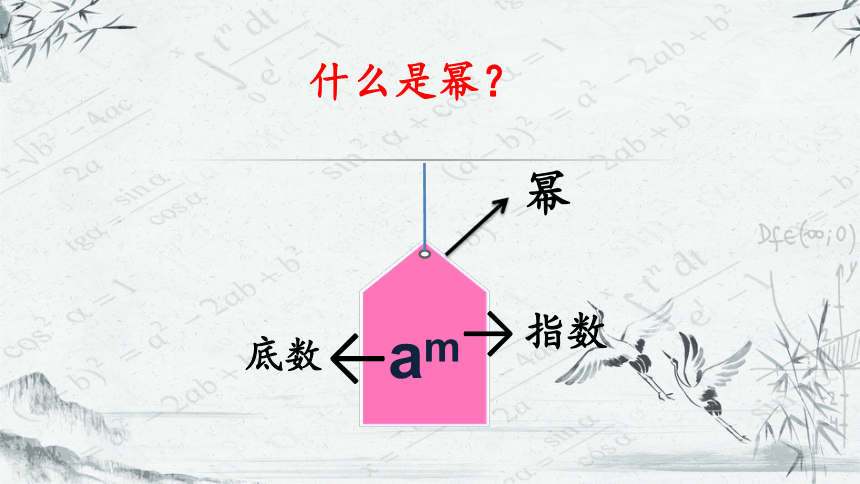
什么是幂?
→
指数
←
底数
幂
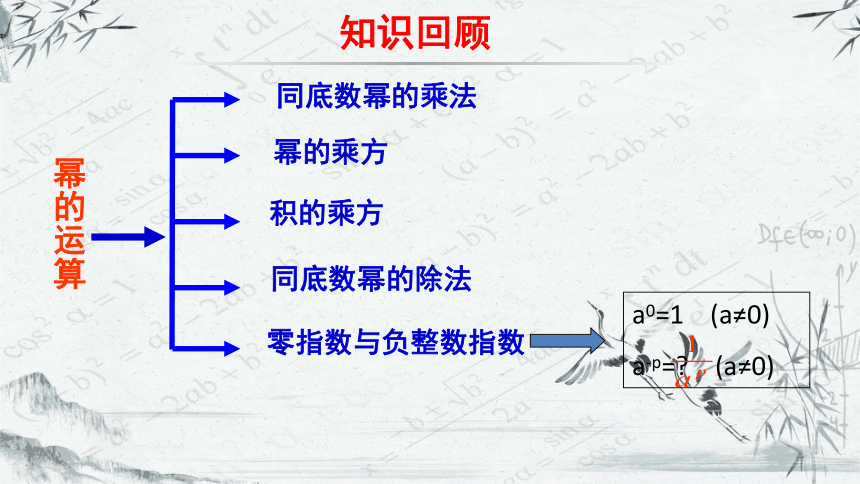
幂的运算
同底数幂的乘法
同底数幂的除法
幂的乘方
积的乘方
零指数与负整数指数
a0=1 (a≠0)
a-p=? (a≠0)
知识回顾
你还记得吗?
1.同底数幂的乘法法则
文字叙述:
同底数幂相乘,底数不变,指数相加
字母表示:
am·an=am+n (m,n是正整数)
扩展:
am·an·ap=am+n+p (m,n,p是正整数)
考考你
a8 .a
x3m .x4m-1 (m是正整数)
(-2)10.(-2)13
-b6.b6
(-a)2 .(-a) .(-a)3
(m+n)3.(m+n)7
=a8+1=a9
=x3m+4m-1=x7m-1
=(-2)10+13=(-2)23=-223
=-b6+6=-b12
=(-a)2+1+3=(-a)6=a6
=(m+n)3+7=(m+n)10
你还记得吗?
2.幂的乘方法则
文字叙述:
幂的乘方,底数不变,指数相乘
字母表示:
(an)m=amn (m,n是正整数)
扩展:
((an)m)p=amnp (m,n,p是正整数)
考考你
(a5)4
-(a8)2
[(-2)3]10
(-bm)7
[(-a)2 ]3 .(a4)2
-[(m-n)3]7
=a5×4=a20
=-a8×2=-a16
=(-2)3×10=(-2)30=230
=-b7m
=(-a)6.a8=a6.a8=a14
=-(m-n)3×7=-(m-n)21
你还记得吗?
3.积的乘方法则
文字叙述:
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘
字母表示:
(ab)n=anbn (n是正整数)
扩展:
(abc)n=anbncn (n是正整数)
考考你
(5a)3
(-xy3)3
(-2a3b6c2)3
-(ab3)2
(0.25)100. (4)100
(2×106)3
=53.a3=125a3
=(-x)3.y9=-x3y9
=(-2)3.a9b18c6=-8a9b18c6
=-a2b6
=(0.25×4)100=1100=1
=23×1018=8×1018
你还记得吗?
4.同底数幂的除法法则
文字叙述:
同底数幂相除,底数不变,指数相减
字母表示:
am÷an=am-n (a≠0 m,n是正整数 m>n)
扩展:
am÷an÷ap=am-n-p (a≠0 m,n,p是整数)
考考你
a8 ÷a3
(?)5÷(?)3
(-s)7÷(-s)2
(m-n)5 ÷(m-n)2
(-3)4÷(-3)2
(-99)8 ÷(-99)8
=(-s)7-2=(-s)5=-s5
=(1/2)5-3=(1/2)2=1/4
=(m-n)5-2=(m-n)3
=a8-3=a5
=(-3)4-2=(-3)2=9
=(-99)8-8=(-99)0=1
你还记得吗?
5.零指数和负指数法则
零指数
任何不等于0的数的0次幂等于1
字母表示:
a0=1 (a≠0)
负指数
任何不等于0的数的-n(n是正整数)次幂,等于这个数的n次幂的倒数
字母表示:
a-p= 1/ ap = (1/a)p (a≠0)
考考你
(-0.003)0
(3x)0 (x≠0)
20170
4-2
(-4)-2
(0.1)-3
=1
=1
=1
=1/42=1/16
=1/(-4)2=1/16
=1/(0.1)3=1/0.001=1000
归纳小结
幂的运算
公式
结论
底数
指数
同底数幂的乘法
am·an=am+n
底数不变
指数相加
同底数幂的除法
am÷an=am-n (a≠0 m,n是正整数 )
底数不变
指数相减
幂的乘方
(an)m=amn (m,n是正整数)
底数不变
指数相乘
归纳:幂的运算有乘除、乘方的运算类型,运算时幂的运算总是转化成指数的运算。那么幂的运算降一级指数的运算,比如同底数幂的乘法除法降一级指数的加减法?,幂的乘方降一级指数的乘法?,掌握了这一规律,各条运算性质就容易记忆,且不会相互混淆
换个方式考考你哦!
a8 .a( )=a 12
a .an .a( )=a n+5
(p-q)5 .(q-p)2
82=2( )=22.2( )
准备好了吗?
4
4
=(p-q)7
6
4
找错误并改正
(1) a3 .a3=2a6
(2) (a3)2=a5
(3) (xy2)3=xy6
(4) (-2b2 )2=-4b4
(5) a8÷a4=a2
(6) (-z)6÷(-z)2=-z4
×
×
×
×
×
×
=a6
=a6
=x3y6
=4b4
=a4
=z4
幂的运算中的方法与技巧
类型一:熟练使用公式,正确进行各种计算
(1)m19÷m14·m3÷m2
(2)(x-y)8÷(x-y)4÷(y-x)3
注意:运算时首先确定所含运算类型,理清运算顺序,用准运算法则
=m5·m3÷m2
=m8÷m2
=m6
或=m19-14+3-2
=m6
=(x-y)4÷(y-x)3
=(y-x)4÷(y-x)3
=y-x
或=(x-y)4÷(y-x)3
=(x-y)4÷[ -(x-y) 3]
=-(x-y)
=y-x
幂的运算中的方法与技巧
类型一:熟练使用公式,正确进行各种计算
(3)(-x2n-2) ·(-x)5÷[xn+1·xn]
(4)4-(-1/2)-2-32÷(-3)0
注意:运算时首先确定所含运算类型,理清运算顺序,用准运算法则
=(-x2n-2 ) ·(-x5) ÷x2n+1
=x2n+3÷x2n+1
=x2
=4-4-9÷1
=4-4-9
=-9
幂的运算中的方法与技巧
类型二:逆用公式进行计算
逆向公式
am+n=am·an
amn= (an)m
anbn= (ab)n
am-n=am÷an
幂的运算中的方法与技巧
类型二:逆用公式进行计算
例1.已知am=4,an=2.
求①am+n的值.②am-n的值.③? a3m+2n的值.④? a2m-n的值
例2.若xn=3,yn=2,则(xy)n的值是多少?(x2y3)n呢?
=am·an
=4×2
=8
=am÷an
=4÷2
=2
=a3m·a2n
=(am)3·(an)2
=43·22
=256
=a2m÷an
=(am)2÷an
=42÷2
=8
(xy)n= xn·yn=3×2=6
(x2y3)n
= x2n·y3n
=(xn)2·(yn) 3
= 32×23
= 9×8=72
幂的运算中的方法与技巧
类型二:逆用公式进行计算
拓展练习:1.(0.125)16×(-8)17
2.24·45·(-0.125)4
=(0.125 )16×(-8)16 ×(-8)
= [0.125 ×(-8)]16 ×(-8)
= (-1)16 ×(-8)
= 1×(-8)
= -8
=24·44·4 ·(-0.125)4
=(2·4)4·4 ·(-0.125)4
=84·4 ·(-0.125)4
= [8 ·(-0.125)]4 ·4
=(-1)4 ·4
=4
幂的运算中的方法与技巧
型三:通过转化底数实现继续运算或求值的目的
例1. 计算(x-y)2(y-x)3??
例2?.如果8m·4m-1=213,求m的值。
= (y-x)2(y-x)3
= (y-x)5
或= (x-y)2[ -(x-y)3 ]
= -(x-y)5
因为8m·4m-1=(23)m
·(22) m-1
=23m·22m-2
=25m-2
=213
所以5m-2=13
,即m=3
幂的运算中的方法与技巧
型三:通过转化底数实现继续运算或求值的目的
拓展练习:1.a4?(-a3)?(-a)3????????
2.(x-y)3(y-x)(y-x)6
3.若2x+3y-4=0,求9x·27y的值.
=a4·(-a3) ·(-a3)
=a4+3+3
=a10
=-(y-x)3(y-x)(y-x)6
=-(y-x)10
解:9x·27y
=(32)x·(33)y
=32x·33y
=32x+3y
因为2x+3y-4=0
,即2x+3y=4
所以原式=32x+3y
=34=81
幂的运算中的方法与技巧
类型四:?比较幂的大小
例1?已知a=355,b=444,c=533,则有(????)
A.a<b<c????B.c<b<a????C.c<a<b????D.a<c<b
解析:化成同指数的,33, 44,55的最大公约数为11,所以把指数统一化成11,则a=(35)11=24311,b=(44)11=25611,c=(53)11=12511.
跟踪练习:若a=8131,b=2741,c=961,比较a、b、c的大小.
两种方法:①化成同底数,比较指数的大小;
②化成同指数,比较底数的大小
解析:化成同底数的,81、 27、9分别可以改写成34、33、32,所以把底数统
一化成3,则a=(34)31=3124,b=(33)41=3123,c=(32)61=3122.
C
因此c<b<a
课堂小结
1、同底数幂的乘法、除法
2、幂的乘方
3、积的乘方
4、零指数和负指数
注意公式的
逆向应用
课程结束,再见!
am
什么是幂?
→
指数
←
底数
幂
幂的运算
同底数幂的乘法
同底数幂的除法
幂的乘方
积的乘方
零指数与负整数指数
a0=1 (a≠0)
a-p=? (a≠0)
知识回顾
你还记得吗?
1.同底数幂的乘法法则
文字叙述:
同底数幂相乘,底数不变,指数相加
字母表示:
am·an=am+n (m,n是正整数)
扩展:
am·an·ap=am+n+p (m,n,p是正整数)
考考你
a8 .a
x3m .x4m-1 (m是正整数)
(-2)10.(-2)13
-b6.b6
(-a)2 .(-a) .(-a)3
(m+n)3.(m+n)7
=a8+1=a9
=x3m+4m-1=x7m-1
=(-2)10+13=(-2)23=-223
=-b6+6=-b12
=(-a)2+1+3=(-a)6=a6
=(m+n)3+7=(m+n)10
你还记得吗?
2.幂的乘方法则
文字叙述:
幂的乘方,底数不变,指数相乘
字母表示:
(an)m=amn (m,n是正整数)
扩展:
((an)m)p=amnp (m,n,p是正整数)
考考你
(a5)4
-(a8)2
[(-2)3]10
(-bm)7
[(-a)2 ]3 .(a4)2
-[(m-n)3]7
=a5×4=a20
=-a8×2=-a16
=(-2)3×10=(-2)30=230
=-b7m
=(-a)6.a8=a6.a8=a14
=-(m-n)3×7=-(m-n)21
你还记得吗?
3.积的乘方法则
文字叙述:
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘
字母表示:
(ab)n=anbn (n是正整数)
扩展:
(abc)n=anbncn (n是正整数)
考考你
(5a)3
(-xy3)3
(-2a3b6c2)3
-(ab3)2
(0.25)100. (4)100
(2×106)3
=53.a3=125a3
=(-x)3.y9=-x3y9
=(-2)3.a9b18c6=-8a9b18c6
=-a2b6
=(0.25×4)100=1100=1
=23×1018=8×1018
你还记得吗?
4.同底数幂的除法法则
文字叙述:
同底数幂相除,底数不变,指数相减
字母表示:
am÷an=am-n (a≠0 m,n是正整数 m>n)
扩展:
am÷an÷ap=am-n-p (a≠0 m,n,p是整数)
考考你
a8 ÷a3
(?)5÷(?)3
(-s)7÷(-s)2
(m-n)5 ÷(m-n)2
(-3)4÷(-3)2
(-99)8 ÷(-99)8
=(-s)7-2=(-s)5=-s5
=(1/2)5-3=(1/2)2=1/4
=(m-n)5-2=(m-n)3
=a8-3=a5
=(-3)4-2=(-3)2=9
=(-99)8-8=(-99)0=1
你还记得吗?
5.零指数和负指数法则
零指数
任何不等于0的数的0次幂等于1
字母表示:
a0=1 (a≠0)
负指数
任何不等于0的数的-n(n是正整数)次幂,等于这个数的n次幂的倒数
字母表示:
a-p= 1/ ap = (1/a)p (a≠0)
考考你
(-0.003)0
(3x)0 (x≠0)
20170
4-2
(-4)-2
(0.1)-3
=1
=1
=1
=1/42=1/16
=1/(-4)2=1/16
=1/(0.1)3=1/0.001=1000
归纳小结
幂的运算
公式
结论
底数
指数
同底数幂的乘法
am·an=am+n
底数不变
指数相加
同底数幂的除法
am÷an=am-n (a≠0 m,n是正整数 )
底数不变
指数相减
幂的乘方
(an)m=amn (m,n是正整数)
底数不变
指数相乘
归纳:幂的运算有乘除、乘方的运算类型,运算时幂的运算总是转化成指数的运算。那么幂的运算降一级指数的运算,比如同底数幂的乘法除法降一级指数的加减法?,幂的乘方降一级指数的乘法?,掌握了这一规律,各条运算性质就容易记忆,且不会相互混淆
换个方式考考你哦!
a8 .a( )=a 12
a .an .a( )=a n+5
(p-q)5 .(q-p)2
82=2( )=22.2( )
准备好了吗?
4
4
=(p-q)7
6
4
找错误并改正
(1) a3 .a3=2a6
(2) (a3)2=a5
(3) (xy2)3=xy6
(4) (-2b2 )2=-4b4
(5) a8÷a4=a2
(6) (-z)6÷(-z)2=-z4
×
×
×
×
×
×
=a6
=a6
=x3y6
=4b4
=a4
=z4
幂的运算中的方法与技巧
类型一:熟练使用公式,正确进行各种计算
(1)m19÷m14·m3÷m2
(2)(x-y)8÷(x-y)4÷(y-x)3
注意:运算时首先确定所含运算类型,理清运算顺序,用准运算法则
=m5·m3÷m2
=m8÷m2
=m6
或=m19-14+3-2
=m6
=(x-y)4÷(y-x)3
=(y-x)4÷(y-x)3
=y-x
或=(x-y)4÷(y-x)3
=(x-y)4÷[ -(x-y) 3]
=-(x-y)
=y-x
幂的运算中的方法与技巧
类型一:熟练使用公式,正确进行各种计算
(3)(-x2n-2) ·(-x)5÷[xn+1·xn]
(4)4-(-1/2)-2-32÷(-3)0
注意:运算时首先确定所含运算类型,理清运算顺序,用准运算法则
=(-x2n-2 ) ·(-x5) ÷x2n+1
=x2n+3÷x2n+1
=x2
=4-4-9÷1
=4-4-9
=-9
幂的运算中的方法与技巧
类型二:逆用公式进行计算
逆向公式
am+n=am·an
amn= (an)m
anbn= (ab)n
am-n=am÷an
幂的运算中的方法与技巧
类型二:逆用公式进行计算
例1.已知am=4,an=2.
求①am+n的值.②am-n的值.③? a3m+2n的值.④? a2m-n的值
例2.若xn=3,yn=2,则(xy)n的值是多少?(x2y3)n呢?
=am·an
=4×2
=8
=am÷an
=4÷2
=2
=a3m·a2n
=(am)3·(an)2
=43·22
=256
=a2m÷an
=(am)2÷an
=42÷2
=8
(xy)n= xn·yn=3×2=6
(x2y3)n
= x2n·y3n
=(xn)2·(yn) 3
= 32×23
= 9×8=72
幂的运算中的方法与技巧
类型二:逆用公式进行计算
拓展练习:1.(0.125)16×(-8)17
2.24·45·(-0.125)4
=(0.125 )16×(-8)16 ×(-8)
= [0.125 ×(-8)]16 ×(-8)
= (-1)16 ×(-8)
= 1×(-8)
= -8
=24·44·4 ·(-0.125)4
=(2·4)4·4 ·(-0.125)4
=84·4 ·(-0.125)4
= [8 ·(-0.125)]4 ·4
=(-1)4 ·4
=4
幂的运算中的方法与技巧
型三:通过转化底数实现继续运算或求值的目的
例1. 计算(x-y)2(y-x)3??
例2?.如果8m·4m-1=213,求m的值。
= (y-x)2(y-x)3
= (y-x)5
或= (x-y)2[ -(x-y)3 ]
= -(x-y)5
因为8m·4m-1=(23)m
·(22) m-1
=23m·22m-2
=25m-2
=213
所以5m-2=13
,即m=3
幂的运算中的方法与技巧
型三:通过转化底数实现继续运算或求值的目的
拓展练习:1.a4?(-a3)?(-a)3????????
2.(x-y)3(y-x)(y-x)6
3.若2x+3y-4=0,求9x·27y的值.
=a4·(-a3) ·(-a3)
=a4+3+3
=a10
=-(y-x)3(y-x)(y-x)6
=-(y-x)10
解:9x·27y
=(32)x·(33)y
=32x·33y
=32x+3y
因为2x+3y-4=0
,即2x+3y=4
所以原式=32x+3y
=34=81
幂的运算中的方法与技巧
类型四:?比较幂的大小
例1?已知a=355,b=444,c=533,则有(????)
A.a<b<c????B.c<b<a????C.c<a<b????D.a<c<b
解析:化成同指数的,33, 44,55的最大公约数为11,所以把指数统一化成11,则a=(35)11=24311,b=(44)11=25611,c=(53)11=12511.
跟踪练习:若a=8131,b=2741,c=961,比较a、b、c的大小.
两种方法:①化成同底数,比较指数的大小;
②化成同指数,比较底数的大小
解析:化成同底数的,81、 27、9分别可以改写成34、33、32,所以把底数统
一化成3,则a=(34)31=3124,b=(33)41=3123,c=(32)61=3122.
C
因此c<b<a
课堂小结
1、同底数幂的乘法、除法
2、幂的乘方
3、积的乘方
4、零指数和负指数
注意公式的
逆向应用
课程结束,再见!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
