苏科版七年级下册数学 第11章《一元一次不等式 复习课 》 课件 (共20张PPT)
文档属性
| 名称 | 苏科版七年级下册数学 第11章《一元一次不等式 复习课 》 课件 (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 355.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览








文档简介
第十一章 一元一次不等式
复习课
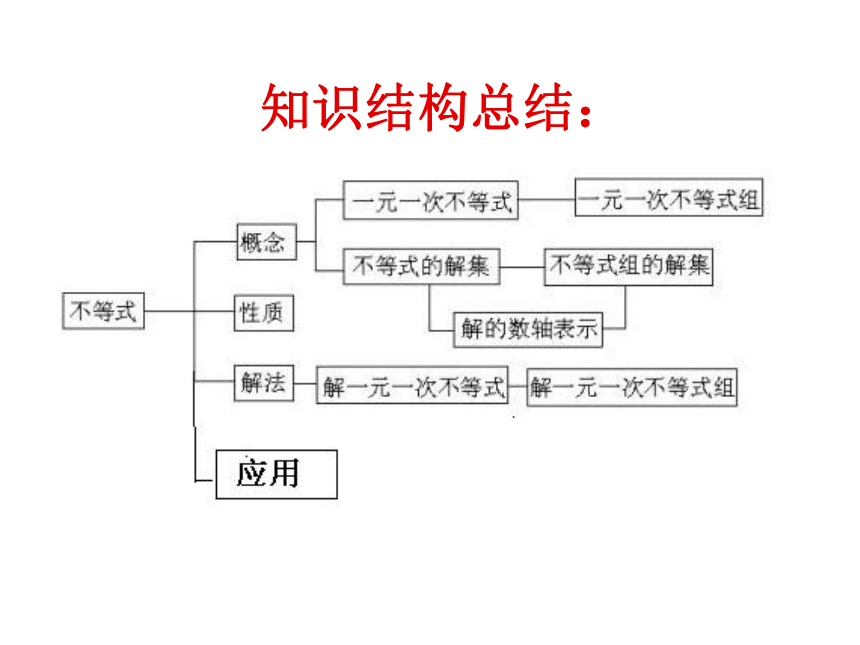
知识结构总结:
(一)
用不等号表示不等关系的式子叫不等式.
“>”“<”“≠”“≤”“≥”
不等式的定义:
一元一次不等式定义:
只含有一个未知数,并且未知数的次数都是1,系数不等于0,这样的不等式叫做一元一次不等式.
一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称这个不等式的解集.
求不等式解集的过程叫做解不等式.
不等式的解集的定义:
用恰当的不等号表示下列关系:
①x的3倍与8的和比y的2倍小: ;
②老师的年龄a不小于你的年龄b: .
列一元一次不等式
解一元一次不等式的一般步骤:
1、去分母
2、去括号
3、移项
4、合并同类项
5、系数化为1
思考:注意事项有哪些
【例】
解不等式 ,
数轴略
一元一次不等式组的定义:
把几个含有同一个未知数的一次不等式联立在一起,就组成了一个一元一次不等式组.
一元一次不等式组解集:
不等式组的解集:
不等式组中所有不等式解集的公共部分,叫做不等式组的解集.
解不等式组:
求不等式组的解集的过程叫做解不等式组.
解一元一次不等式组的一般步骤:
1、解不等式①得
2、解不等式②得
3、在数轴上表示①、②的解集
4、写出不等式组的解集
解不等式或不等式组,并在数轴上表示解集
口诀:同大取大;同小取小;大小小大中间找,
大大小小找不了.
一元一次不等式的应用
例1、代数式 的值不大于 的值,求的范围
例2、方程组 的解为负数,求 的范围.
例3、已知 满足 ,化简.
.练习: 已知关于x的不等式组 的解集为3≤x<5,:求 的值?
例题4:三角形的三边长分别是3、(1-2a)、8,求a的取值范围.
例题5:某公司到果品基地购买某种优质水果慰问医务工作者,果品基地对购买量在3000kg以上(含3000kg)的顾客采用两种销售方案。
甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回。已知该公司租车从基地到公司的运输费用为5000元。
(1)分别写出该公司两种购买方案付款金额(元)用所购买的水果数量x(kg)的代数式表示。
(2)如果是你购买,你会选择哪种购买方案付款最少?并说明理由
1. 不等式组
的正整数解的个数是:
A、1 B、2 C、3 D、0
2. 若不等式组
的解集为x>3,则m的取值范围是:
A、m≥3 B、m=3 C、m<3 D、m≤3
小练:一元一次不等式单元检测
四、课堂小结
这节课你有什么收获?你觉得在哪些方面需要注意什么?
五、布置作业
课课练一元一次不等式复习A、B组
复习课
知识结构总结:
(一)
用不等号表示不等关系的式子叫不等式.
“>”“<”“≠”“≤”“≥”
不等式的定义:
一元一次不等式定义:
只含有一个未知数,并且未知数的次数都是1,系数不等于0,这样的不等式叫做一元一次不等式.
一个含有未知数的不等式的所有的解,组成这个不等式的解的集合,简称这个不等式的解集.
求不等式解集的过程叫做解不等式.
不等式的解集的定义:
用恰当的不等号表示下列关系:
①x的3倍与8的和比y的2倍小: ;
②老师的年龄a不小于你的年龄b: .
列一元一次不等式
解一元一次不等式的一般步骤:
1、去分母
2、去括号
3、移项
4、合并同类项
5、系数化为1
思考:注意事项有哪些
【例】
解不等式 ,
数轴略
一元一次不等式组的定义:
把几个含有同一个未知数的一次不等式联立在一起,就组成了一个一元一次不等式组.
一元一次不等式组解集:
不等式组的解集:
不等式组中所有不等式解集的公共部分,叫做不等式组的解集.
解不等式组:
求不等式组的解集的过程叫做解不等式组.
解一元一次不等式组的一般步骤:
1、解不等式①得
2、解不等式②得
3、在数轴上表示①、②的解集
4、写出不等式组的解集
解不等式或不等式组,并在数轴上表示解集
口诀:同大取大;同小取小;大小小大中间找,
大大小小找不了.
一元一次不等式的应用
例1、代数式 的值不大于 的值,求的范围
例2、方程组 的解为负数,求 的范围.
例3、已知 满足 ,化简.
.练习: 已知关于x的不等式组 的解集为3≤x<5,:求 的值?
例题4:三角形的三边长分别是3、(1-2a)、8,求a的取值范围.
例题5:某公司到果品基地购买某种优质水果慰问医务工作者,果品基地对购买量在3000kg以上(含3000kg)的顾客采用两种销售方案。
甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回。已知该公司租车从基地到公司的运输费用为5000元。
(1)分别写出该公司两种购买方案付款金额(元)用所购买的水果数量x(kg)的代数式表示。
(2)如果是你购买,你会选择哪种购买方案付款最少?并说明理由
1. 不等式组
的正整数解的个数是:
A、1 B、2 C、3 D、0
2. 若不等式组
的解集为x>3,则m的取值范围是:
A、m≥3 B、m=3 C、m<3 D、m≤3
小练:一元一次不等式单元检测
四、课堂小结
这节课你有什么收获?你觉得在哪些方面需要注意什么?
五、布置作业
课课练一元一次不等式复习A、B组
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
