苏科版七年级下册数学《11.4解一元一次不等式》(6) (共28张PPT)
文档属性
| 名称 | 苏科版七年级下册数学《11.4解一元一次不等式》(6) (共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 10:58:26 | ||
图片预览




文档简介
第九章 不等式与不等式组
9.2 一元一次不等式
第1课时 一元一次不等式的解法
新人教版 七年级
1.理解和掌握一元一次不等式的概念;
2.会用不等式的性质熟练地解一元一次不等式.(重点、
难点)
学习目标
课前复习
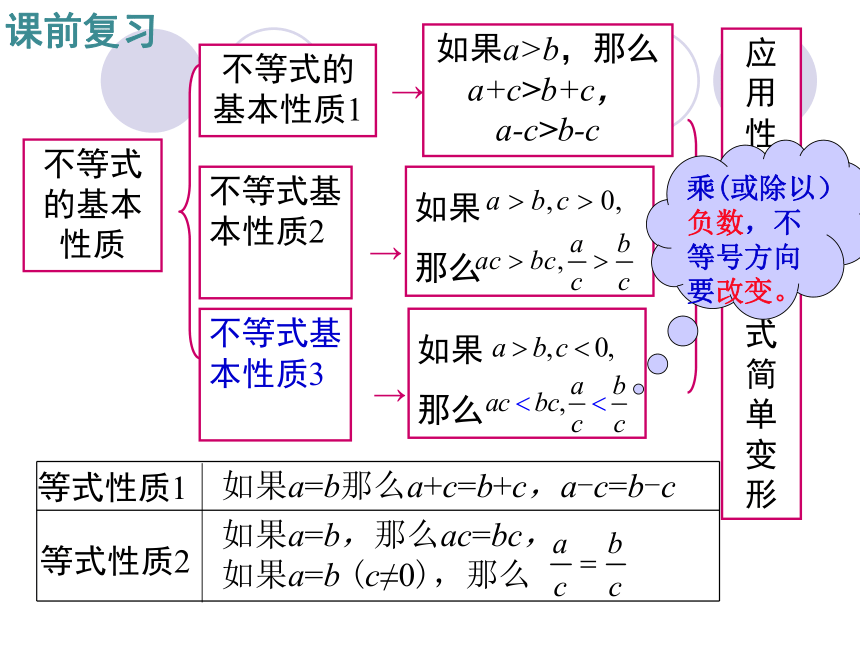
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
→
如果 那么
如果 那么
应用性质对不等式简单变形
不等式的基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
如果a=b那么a+c=b+c,a-c=b-c
如果a=b,那么ac=bc,
如果a=b (c≠0),那么
等式性质1
等式性质2
乘(或除以)负数,不等号方向要改变。
课前小测
1、解下列方程,并归纳解一元一次方程的步骤和注意点
(2) ;
X=2
X=2
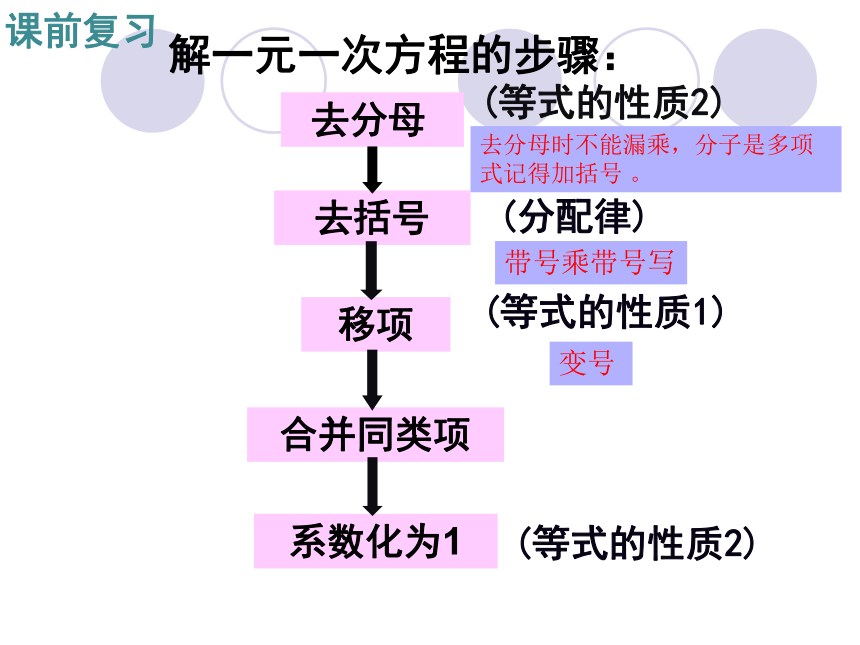
解一元一次方程的步骤:
移项
合并同类项
系数化为1
去括号
(分配律)
(等式的性质1)
(等式的性质2)
去分母
(等式的性质2)
课前复习
去分母时不能漏乘,分子是多项式记得加括号 。
带号乘带号写
变号
2. 已知a < b,用“>”或“<”填空:
(1)2a -5 2b -5 ;
(2)-3.5a+1 -3.5b+1 .
<
>
课前小测
C
3.
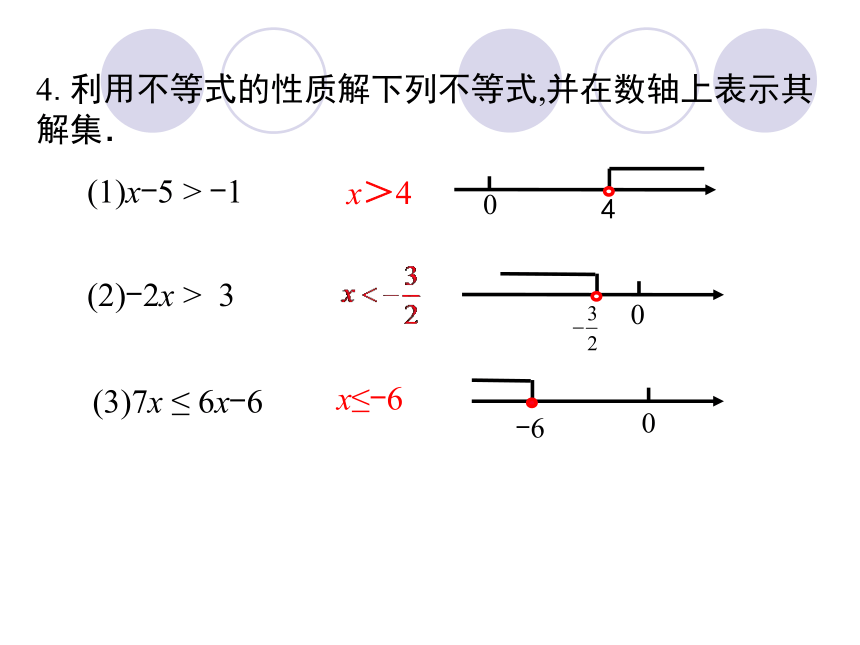
4.利用不等式的性质解下列不等式,并在数轴上表示其解集.
(2)-2x > 3
(1)x-5 > -1
(3)7x ≤ 6x-6
x>4
x≤-6
4
0
0
0
-6
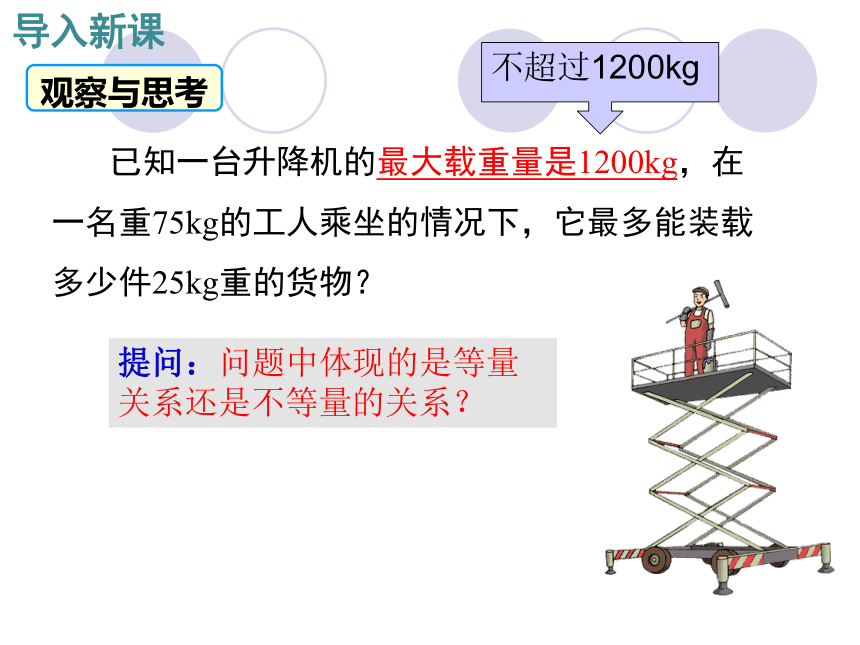
导入新课
已知一台升降机的最大载重量是1200kg,在
一名重75kg的工人乘坐的情况下,它最多能装载
多少件25kg重的货物?
观察与思考
不超过1200kg
提问:问题中体现的是等量关系还是不等量的关系?
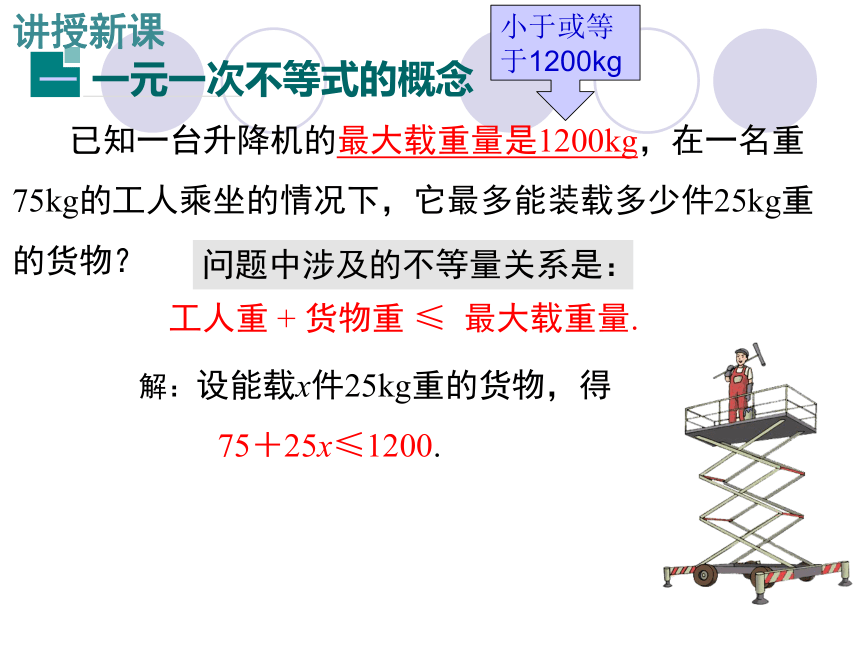
问题中涉及的不等量关系是:
解:设能载x件25kg重的货物,得
75+25x≤1200.
工人重 + 货物重 ≤ 最大载重量.
一元一次不等式的概念
一
讲授新课
已知一台升降机的最大载重量是1200kg,在一名重75kg的工人乘坐的情况下,它最多能装载多少件25kg重的货物?
小于或等于1200kg
只含有一个未知数,且未知数的次数是1的不等式,称为一元一次不等式.
像75 + 25x ≤1200 这样,
它与一元一次方程的定义有什么共同点吗?
不等式具有什么特征?
一元一次不等式的概念
一
讲授新课
下列不等式中,哪些是一元一次不等式?
(1) 3x+2>x–1 (2)5x+3<0
(3) (4)x(x–1)<2x
?
?
?
?
左边不是整式
化简后是
x2-x<2x
针对训练1
一元一次不等式的概念
一
例1 已知 是关于x的一元一次不等式,
则a的值是________.
典例精析
1
2a-1=1
a=1
一元一次不等式的概念
一
针对训练2
一元一次不等式的概念
一
解不等式:
4x-1<5x+15
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
解一元一次不等式
二
等式性质1
等式性质2
不等式性质1
不等式性质3
讲授新课
例2 解下列一元一次不等式, 并把它的解集在数轴上表示出来:
典例精析
怎样解这个不等式呢?
解一元一次不等式
二
解:
首先将分母去掉
去括号,得 2x-10+6≤9x
去分母,得 2(x-5)+1×6≤9x
移项,得 2x-9x≤10-6
去括号
将同类项放在一起
不等式
合并同类项,得 -7x ≤4
化未知数的系数为1,得
x≥ .
计算结果
根据不等式性质3
0
原不等式的解集为 ,在数轴上表示为
界点实心还是空心?
解一元一次不等式
二
解一元一次不等式与解一元一次方程的步骤和依据有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
议一议
相同点:它们的步骤基本相同,都是去分母、去括号、
移项、合并同类项、未知数的系数化为1。
注意点:这些步骤中,要特别注意的是:不等式两边都乘(或除
以)同一个负数,必须改 变不等号的方向.这是与解一
元一次方程 不同的地方。
不同点:它们的依据不相同.解一元一次方程的依据是等
式的性质,解一元一次不等式的依据是不等式
的。
归纳
解一元一次不等式
二
题组一
第1组
第2组
解不等式大PK
解下列不等式,并把它们的解集在数轴上表示出来:
解一元一次不等式
二
解
解得 x ≤ 6.
x≤6在数轴上表示如图所示.
-1
0
1
2
3
4
5
6
所以,当x≤6时,代数式 x+2的值大于或等于0.
由图可知,满足条件的正整数有 1,2,3,4,5,6.
例3 当x取什么值时,代数式 x +2的值不小于0?并求出所有满足条件的正整数.
根据题意,得 x +2≥ 0,
满足条件的非负整数呢?
求不等式的特殊解
三
求不等式的特殊解:
1、先要准确求出不等式的解集。
2、再确定特殊解。
注意点:在确定特殊解时,一定要注意是否包
括端点的值,一般可以结合数轴,形
象直观,一目了然。
方法总结
求不等式的特殊解
三
针对训练3
求不等式的特殊解
三
解:把x=3代入ax+12=0中,
得 a=-4.
把a=-4代入(a+2)x>-6中,
得-2x>-6,
解得x<3.
在数轴上表示如图:
∴正整数解有1和2.
已知方程ax+12=0的解是x=3,求关于x不等式(a+2)x>-6的解集,并在数轴上表示出来,其中正整数解有哪些?
-1
0
1
2
3
4
5
6
题组二
不等式与方程的联系
四
【变式】已知不等式 x+8>4x+m (m是常数)的解集是
x<3,求 m.
方法总结:已知解集求字母系数的值,通常是先解含有字母的不等式,再利用解集的唯一性列方程求字母的值.解题过程体现了方程思想.
不等式与方程的联系
四
课堂检测
1、
2、
3、
3、
4、
课堂小结
一元一次不等式的解法
一元一次不等式的定义
步骤
解一元一次不等式
→
特殊解
→
一元一次不等式与方程的联系
布置作业
1、课内作业:P126 1(2)、(4)、(6)
(写在作业本)
2、课外作业:《学练优》本节练习
3、预习新课: 课本P124-125
9.2 一元一次不等式
第1课时 一元一次不等式的解法
新人教版 七年级
1.理解和掌握一元一次不等式的概念;
2.会用不等式的性质熟练地解一元一次不等式.(重点、
难点)
学习目标
课前复习
不等式的基本性质
不等式基本性质2
不等式基本性质3
→
→
如果 那么
如果 那么
应用性质对不等式简单变形
不等式的基本性质1
如果a>b,那么a+c>b+c,
a-c>b-c
→
如果a=b那么a+c=b+c,a-c=b-c
如果a=b,那么ac=bc,
如果a=b (c≠0),那么
等式性质1
等式性质2
乘(或除以)负数,不等号方向要改变。
课前小测
1、解下列方程,并归纳解一元一次方程的步骤和注意点
(2) ;
X=2
X=2
解一元一次方程的步骤:
移项
合并同类项
系数化为1
去括号
(分配律)
(等式的性质1)
(等式的性质2)
去分母
(等式的性质2)
课前复习
去分母时不能漏乘,分子是多项式记得加括号 。
带号乘带号写
变号
2. 已知a < b,用“>”或“<”填空:
(1)2a -5 2b -5 ;
(2)-3.5a+1 -3.5b+1 .
<
>
课前小测
C
3.
4.利用不等式的性质解下列不等式,并在数轴上表示其解集.
(2)-2x > 3
(1)x-5 > -1
(3)7x ≤ 6x-6
x>4
x≤-6
4
0
0
0
-6
导入新课
已知一台升降机的最大载重量是1200kg,在
一名重75kg的工人乘坐的情况下,它最多能装载
多少件25kg重的货物?
观察与思考
不超过1200kg
提问:问题中体现的是等量关系还是不等量的关系?
问题中涉及的不等量关系是:
解:设能载x件25kg重的货物,得
75+25x≤1200.
工人重 + 货物重 ≤ 最大载重量.
一元一次不等式的概念
一
讲授新课
已知一台升降机的最大载重量是1200kg,在一名重75kg的工人乘坐的情况下,它最多能装载多少件25kg重的货物?
小于或等于1200kg
只含有一个未知数,且未知数的次数是1的不等式,称为一元一次不等式.
像75 + 25x ≤1200 这样,
它与一元一次方程的定义有什么共同点吗?
不等式具有什么特征?
一元一次不等式的概念
一
讲授新课
下列不等式中,哪些是一元一次不等式?
(1) 3x+2>x–1 (2)5x+3<0
(3) (4)x(x–1)<2x
?
?
?
?
左边不是整式
化简后是
x2-x<2x
针对训练1
一元一次不等式的概念
一
例1 已知 是关于x的一元一次不等式,
则a的值是________.
典例精析
1
2a-1=1
a=1
一元一次不等式的概念
一
针对训练2
一元一次不等式的概念
一
解不等式:
4x-1<5x+15
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
解一元一次不等式
二
等式性质1
等式性质2
不等式性质1
不等式性质3
讲授新课
例2 解下列一元一次不等式, 并把它的解集在数轴上表示出来:
典例精析
怎样解这个不等式呢?
解一元一次不等式
二
解:
首先将分母去掉
去括号,得 2x-10+6≤9x
去分母,得 2(x-5)+1×6≤9x
移项,得 2x-9x≤10-6
去括号
将同类项放在一起
不等式
合并同类项,得 -7x ≤4
化未知数的系数为1,得
x≥ .
计算结果
根据不等式性质3
0
原不等式的解集为 ,在数轴上表示为
界点实心还是空心?
解一元一次不等式
二
解一元一次不等式与解一元一次方程的步骤和依据有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
议一议
相同点:它们的步骤基本相同,都是去分母、去括号、
移项、合并同类项、未知数的系数化为1。
注意点:这些步骤中,要特别注意的是:不等式两边都乘(或除
以)同一个负数,必须改 变不等号的方向.这是与解一
元一次方程 不同的地方。
不同点:它们的依据不相同.解一元一次方程的依据是等
式的性质,解一元一次不等式的依据是不等式
的。
归纳
解一元一次不等式
二
题组一
第1组
第2组
解不等式大PK
解下列不等式,并把它们的解集在数轴上表示出来:
解一元一次不等式
二
解
解得 x ≤ 6.
x≤6在数轴上表示如图所示.
-1
0
1
2
3
4
5
6
所以,当x≤6时,代数式 x+2的值大于或等于0.
由图可知,满足条件的正整数有 1,2,3,4,5,6.
例3 当x取什么值时,代数式 x +2的值不小于0?并求出所有满足条件的正整数.
根据题意,得 x +2≥ 0,
满足条件的非负整数呢?
求不等式的特殊解
三
求不等式的特殊解:
1、先要准确求出不等式的解集。
2、再确定特殊解。
注意点:在确定特殊解时,一定要注意是否包
括端点的值,一般可以结合数轴,形
象直观,一目了然。
方法总结
求不等式的特殊解
三
针对训练3
求不等式的特殊解
三
解:把x=3代入ax+12=0中,
得 a=-4.
把a=-4代入(a+2)x>-6中,
得-2x>-6,
解得x<3.
在数轴上表示如图:
∴正整数解有1和2.
已知方程ax+12=0的解是x=3,求关于x不等式(a+2)x>-6的解集,并在数轴上表示出来,其中正整数解有哪些?
-1
0
1
2
3
4
5
6
题组二
不等式与方程的联系
四
【变式】已知不等式 x+8>4x+m (m是常数)的解集是
x<3,求 m.
方法总结:已知解集求字母系数的值,通常是先解含有字母的不等式,再利用解集的唯一性列方程求字母的值.解题过程体现了方程思想.
不等式与方程的联系
四
课堂检测
1、
2、
3、
3、
4、
课堂小结
一元一次不等式的解法
一元一次不等式的定义
步骤
解一元一次不等式
→
特殊解
→
一元一次不等式与方程的联系
布置作业
1、课内作业:P126 1(2)、(4)、(6)
(写在作业本)
2、课外作业:《学练优》本节练习
3、预习新课: 课本P124-125
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
