苏科版七年级下册数学《11.6一元一次不等式组》(2) (共21张PPT)
文档属性
| 名称 | 苏科版七年级下册数学《11.6一元一次不等式组》(2) (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 792.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 00:00:00 | ||
图片预览







文档简介
9.3一元一次不等式组的应用
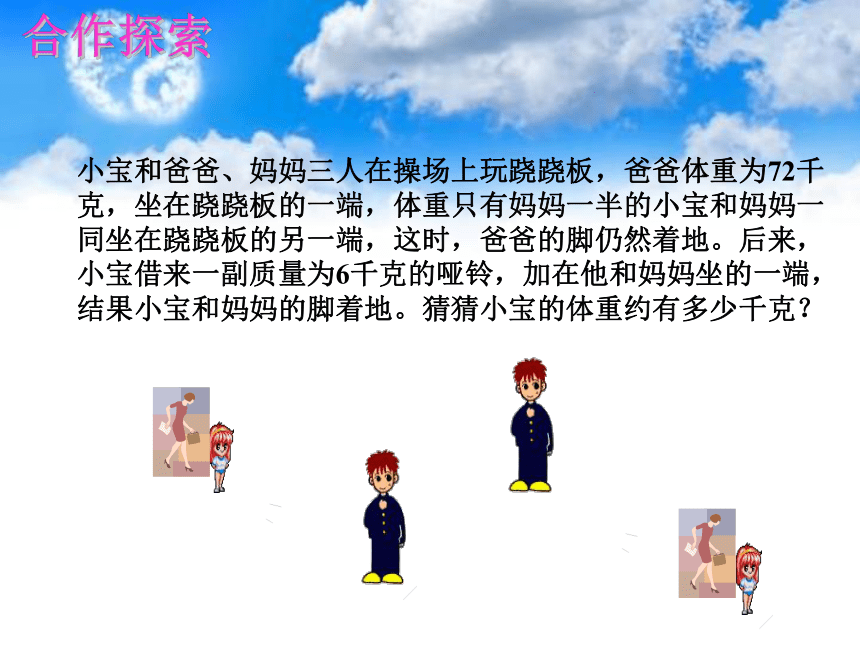
小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时,爸爸的脚仍然着地。后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果小宝和妈妈的脚着地。猜猜小宝的体重约有多少千克?
合作探索
分析:从跷跷板的两种状况可以得到不等关系
妈妈的体重+小宝的体重 爸爸的体重
妈妈的体重+小宝的体重+6千克 爸爸的体重
解:设小宝的体重是x千克,则妈妈的体重是2x千克。
由题意得
<
>
2x+x<72
2x+x+6>72
解得:22例1:3个小组计划在10天内生产500件产品(每天产量
相同),按原先的生产速度,不能完成任务;如果每
个小组每天比原先多生产1件产品,就能提前完成任务;
问:每个小组原先每天生产多少件产品?
1、“不能完成任务”的意思是:
2、“提前完成任务”的意思是:
按原先的生产速度,10天的产品数量 500
提高生产速度后,10天的产品数量 500
思路分析
例题讲解1:列一元一次不等式组解决实际问题
<
>
例1 3个小组计划在10天内生产500件产品(每
天生产量相同),按原先的生产速度,不能完
成任务;如果每个小组每天比原先多生产1产品,
就能提前完成任务.每个小组原先每天生产多少
件产品?
解:设每个小组原先每天生产x件产品,根据题
意,得
①
②
由不等式①得
由不等式②得
因此,不等式组的解集为
根据题意,x的值应是整数,所以x=16
答:每个小组原先每天生产16件产品.
(1)审 :审题,分析题目中已知什么,求什么,明确各数量之间的关系;
(2)设:设适当的未知数;
(3)找:找出题目中的所有不等关系;
(4)列:根据不等关系列出不等式组;
(5)解:解不等式组,要注意对结果适当取舍,
使答案符合实际情况;
(6)答:写出符合题意的答案。
列不等式组解应用题的一般步骤:
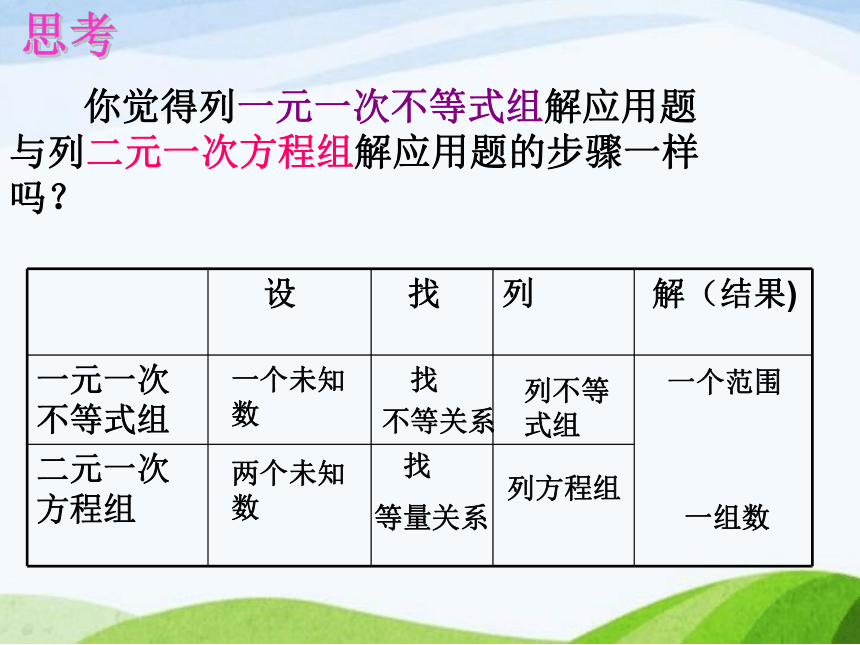
你觉得列一元一次不等式组解应用题与列二元一次方程组解应用题的步骤一样吗?
设
找
列
解(结果)
一元一次不等式组
二元一次方程组
一个未知数
两个未知数
找
不等关系
找
等量关系
一个范围
一组数
列不等
式组
列方程组
思考
练习1 一本英语书共98页,张力读了一周(7天)还没读完,而李永不到一周就已读完。李永平均每天比张力多读3页,张力平均每天读多少页?(答案取整数)
活学活用
解:设张力平均每天读x页
7( x +3)>98 ①
7 x <98 ②
解不等式①得
x >11
解不等式②得
x <14
因此,不等式组的解集为
11 < x<14
根据题意得,x的值应是整数,所以
x=12或13
答:张力平均每天读12或13页
练习2 如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人分到桃子但少于3个.试问有几个学生,几个桃子?
活学活用
设有x个学生,
整理得:
解得:
∵x表示人数
(3x+8)
(3x+8)-5(x-1) <3
2x<13
2x>10
x<6.5
x>5
即:5<x<6.5
∴ 3x+8=
解:
答:共有6个学生,26个桃子。
如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人得到桃子但少于3个.试问有几个学生,几个桃子?
则有(3x+8)个桃子.
5(x-1)
>0
-
∴x取正整数
∴ x=6
26
某商店需要购进甲、乙两种商品共120件,其
进价和售价如下表:(注:获利=售价-进价)
例题讲解2:运用不等式组解决实际应用中的方案设计问题
甲
乙
进价(元/件)
15
35
售价(元/件)
20
45
(1)若商店计划销售完这批商品后能获利1000元,
请问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4000元,且销售完这
批商品后获利多于1135元,请问有哪几种购货方案?
并指出获利最大的购货方案.
设甲种商品应购进x件,乙种商品应购进y件.
根据题意得:
x+y=120
5x+10y=1000
解得: x=40
y=80
答:甲种商品购进40件,乙种商品购进80件.
(2)设甲种商品购进a件,则乙种商品购进(120-a)件.
根据题意得
15a+35(120-a)<4000
5a+10(120-a)>1135
解不等式组,得10∵a为非负整数,
∴a取11,12.
方案一:甲种商品购进11件,乙种商品购进109件.
方案二:甲种商品购进12件,乙种商品购进108件.
答:有两种购货方案,其中获利最大的是方案二.
求实际问题中方案的种类或最大值(最小值)问题的方法:
常通过求不等式(组)的解集,分类讨论找出答案,即先根据题意,设出未知数,列出不等式(组),求出相应的取值范围,再根据题目的条件分类讨论,求出答案。
归纳总结:
为了更好的保护美丽图画的邛海湿地,
西昌市污水处理厂决定先购买A、B两型
污水处理设备共20台,对邛海湿地周边
污水进行处理,每台A型污水处理设备
12万元,每台B型污水处理设备10万元.
已知1台A型污水处理设备和2台B型污水
处理设备每周可以处理污水640吨,2台
A型污水处理设备和3台B型污水处理设备
每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,
每周处理污水的量不低于4500吨,请你列举出所有购买方案,
并指出哪种方案所需资金最少?最少是多少?
走近中考
(1)设A型污水处理设备每周每台可以处理污水x吨,B型污水处理设备每周每台可以处理污水y吨,
x+2y=640
2x+3y=1080
解得,
x=240
y=200
即A型污水处理设备每周每台可以处理污水240吨,B型污水处理设备每周每台可以处理污水200吨;
(2)设购买A型污水处理设备x台,则购买B型污水处理设备(20-x)台,
则
12x+10(20-x)≤230
240x+200(20-x)≥4500
解得,12.5≤x≤15,
第一种方案:当x=13时,20-x=7,花费的费用为:13×12+7×10=226万元;
第二种方案:当x=14时,20-x=6,花费的费用为:14×12+6×10=228万元;
第三种方案;当x=15时,20-x=5,花费的费用为:15×12+5×10=230万元;
即购买A型污水处理设备13台,则购买B型污水处理设备7台时,所需购买资金最少,最少是226万元.
展示交流
展
示
交
流
应用一元一次不等式组解决实际问题的一般思路:
实际问题
不等关系
不等式
不等式组
结合实际因素
找出
列出
组成
求 解
解决
归纳
谈谈你今天的收获!
(1)列不等式组解应用题的一般步骤有哪些?它与列
二元一次方程组解应用题的有哪些异同?
(2)一元一次不等式组的应用运用了哪些数学思想?
知识回顾
数学建模思想和分类讨论思想
数学建模思想是对日常生活和社会中的实际问题进行抽象化,
建立数学模型。数学建模旨在拓展思维空间,让数学贴近现实生
活,从而进行数学知识和实际生活双向建构的过程中,体会到数
学的价值,享受学习数学的乐趣。
必做题:习题9.3第5﹑6题;
选做题:复习题9第7﹑8题。
作业布置
期待后续学习.....
谢谢欣赏!
小宝和爸爸、妈妈三人在操场上玩跷跷板,爸爸体重为72千克,坐在跷跷板的一端,体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端,这时,爸爸的脚仍然着地。后来,小宝借来一副质量为6千克的哑铃,加在他和妈妈坐的一端,结果小宝和妈妈的脚着地。猜猜小宝的体重约有多少千克?
合作探索
分析:从跷跷板的两种状况可以得到不等关系
妈妈的体重+小宝的体重 爸爸的体重
妈妈的体重+小宝的体重+6千克 爸爸的体重
解:设小宝的体重是x千克,则妈妈的体重是2x千克。
由题意得
<
>
2x+x<72
2x+x+6>72
解得:22
相同),按原先的生产速度,不能完成任务;如果每
个小组每天比原先多生产1件产品,就能提前完成任务;
问:每个小组原先每天生产多少件产品?
1、“不能完成任务”的意思是:
2、“提前完成任务”的意思是:
按原先的生产速度,10天的产品数量 500
提高生产速度后,10天的产品数量 500
思路分析
例题讲解1:列一元一次不等式组解决实际问题
<
>
例1 3个小组计划在10天内生产500件产品(每
天生产量相同),按原先的生产速度,不能完
成任务;如果每个小组每天比原先多生产1产品,
就能提前完成任务.每个小组原先每天生产多少
件产品?
解:设每个小组原先每天生产x件产品,根据题
意,得
①
②
由不等式①得
由不等式②得
因此,不等式组的解集为
根据题意,x的值应是整数,所以x=16
答:每个小组原先每天生产16件产品.
(1)审 :审题,分析题目中已知什么,求什么,明确各数量之间的关系;
(2)设:设适当的未知数;
(3)找:找出题目中的所有不等关系;
(4)列:根据不等关系列出不等式组;
(5)解:解不等式组,要注意对结果适当取舍,
使答案符合实际情况;
(6)答:写出符合题意的答案。
列不等式组解应用题的一般步骤:
你觉得列一元一次不等式组解应用题与列二元一次方程组解应用题的步骤一样吗?
设
找
列
解(结果)
一元一次不等式组
二元一次方程组
一个未知数
两个未知数
找
不等关系
找
等量关系
一个范围
一组数
列不等
式组
列方程组
思考
练习1 一本英语书共98页,张力读了一周(7天)还没读完,而李永不到一周就已读完。李永平均每天比张力多读3页,张力平均每天读多少页?(答案取整数)
活学活用
解:设张力平均每天读x页
7( x +3)>98 ①
7 x <98 ②
解不等式①得
x >11
解不等式②得
x <14
因此,不等式组的解集为
11 < x<14
根据题意得,x的值应是整数,所以
x=12或13
答:张力平均每天读12或13页
练习2 如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人分到桃子但少于3个.试问有几个学生,几个桃子?
活学活用
设有x个学生,
整理得:
解得:
∵x表示人数
(3x+8)
(3x+8)-5(x-1) <3
2x<13
2x>10
x<6.5
x>5
即:5<x<6.5
∴ 3x+8=
解:
答:共有6个学生,26个桃子。
如果每个学生分3个桃子,那么多8个;如果前面每人分5个,那么最后一个人得到桃子但少于3个.试问有几个学生,几个桃子?
则有(3x+8)个桃子.
5(x-1)
>0
-
∴x取正整数
∴ x=6
26
某商店需要购进甲、乙两种商品共120件,其
进价和售价如下表:(注:获利=售价-进价)
例题讲解2:运用不等式组解决实际应用中的方案设计问题
甲
乙
进价(元/件)
15
35
售价(元/件)
20
45
(1)若商店计划销售完这批商品后能获利1000元,
请问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4000元,且销售完这
批商品后获利多于1135元,请问有哪几种购货方案?
并指出获利最大的购货方案.
设甲种商品应购进x件,乙种商品应购进y件.
根据题意得:
x+y=120
5x+10y=1000
解得: x=40
y=80
答:甲种商品购进40件,乙种商品购进80件.
(2)设甲种商品购进a件,则乙种商品购进(120-a)件.
根据题意得
15a+35(120-a)<4000
5a+10(120-a)>1135
解不等式组,得10
∴a取11,12.
方案一:甲种商品购进11件,乙种商品购进109件.
方案二:甲种商品购进12件,乙种商品购进108件.
答:有两种购货方案,其中获利最大的是方案二.
求实际问题中方案的种类或最大值(最小值)问题的方法:
常通过求不等式(组)的解集,分类讨论找出答案,即先根据题意,设出未知数,列出不等式(组),求出相应的取值范围,再根据题目的条件分类讨论,求出答案。
归纳总结:
为了更好的保护美丽图画的邛海湿地,
西昌市污水处理厂决定先购买A、B两型
污水处理设备共20台,对邛海湿地周边
污水进行处理,每台A型污水处理设备
12万元,每台B型污水处理设备10万元.
已知1台A型污水处理设备和2台B型污水
处理设备每周可以处理污水640吨,2台
A型污水处理设备和3台B型污水处理设备
每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,
每周处理污水的量不低于4500吨,请你列举出所有购买方案,
并指出哪种方案所需资金最少?最少是多少?
走近中考
(1)设A型污水处理设备每周每台可以处理污水x吨,B型污水处理设备每周每台可以处理污水y吨,
x+2y=640
2x+3y=1080
解得,
x=240
y=200
即A型污水处理设备每周每台可以处理污水240吨,B型污水处理设备每周每台可以处理污水200吨;
(2)设购买A型污水处理设备x台,则购买B型污水处理设备(20-x)台,
则
12x+10(20-x)≤230
240x+200(20-x)≥4500
解得,12.5≤x≤15,
第一种方案:当x=13时,20-x=7,花费的费用为:13×12+7×10=226万元;
第二种方案:当x=14时,20-x=6,花费的费用为:14×12+6×10=228万元;
第三种方案;当x=15时,20-x=5,花费的费用为:15×12+5×10=230万元;
即购买A型污水处理设备13台,则购买B型污水处理设备7台时,所需购买资金最少,最少是226万元.
展示交流
展
示
交
流
应用一元一次不等式组解决实际问题的一般思路:
实际问题
不等关系
不等式
不等式组
结合实际因素
找出
列出
组成
求 解
解决
归纳
谈谈你今天的收获!
(1)列不等式组解应用题的一般步骤有哪些?它与列
二元一次方程组解应用题的有哪些异同?
(2)一元一次不等式组的应用运用了哪些数学思想?
知识回顾
数学建模思想和分类讨论思想
数学建模思想是对日常生活和社会中的实际问题进行抽象化,
建立数学模型。数学建模旨在拓展思维空间,让数学贴近现实生
活,从而进行数学知识和实际生活双向建构的过程中,体会到数
学的价值,享受学习数学的乐趣。
必做题:习题9.3第5﹑6题;
选做题:复习题9第7﹑8题。
作业布置
期待后续学习.....
谢谢欣赏!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
