苏科版数学八年级下册 10.1分式 (共28张PPT)
文档属性
| 名称 | 苏科版数学八年级下册 10.1分式 (共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览







文档简介
10.1 分式
复习回顾:
单项式、多项式、整式:
说明:单独一个数或一个字母也是单项式.
3、单项式和多项式统称为整式.
1、数与字母乘积的代数式叫做单项式.
例:2,x,2x,2x2y2, ,...
2、几个单项式的和叫做多项式.
例:x+y,x2+y2+z3+1,πR2-πr2, 都是多项式
1、如果某市人口总数为a人,绿地面积为bm2 ,
那么该市人均拥有绿地 m2;
问题情境
2、如果一块长方形玻璃板的面积为2m2,这块玻璃板的宽为am,那么它的长是 m;
3、如果面积为a公顷、b公顷的两块棉田分别产棉花m千克、n千克,那么这两块棉田平均每公顷产棉花______千克.
讨论
像 、 、 …… 这样的式子有什么
共同特征?
它们与整式有什么区别?
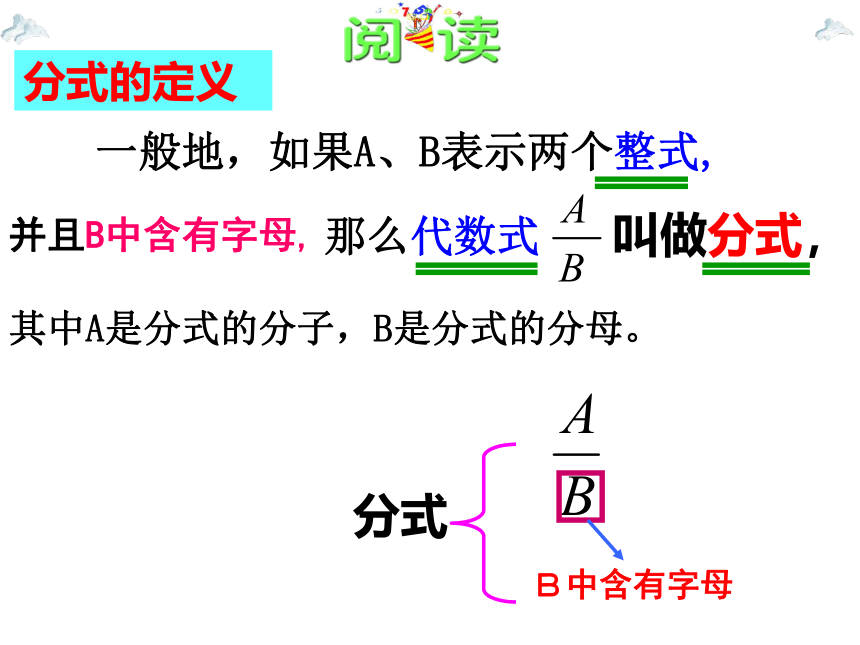
一般地,如果A、B表示两个整式,
分式的定义
并且B中含有字母,
那么代数式
叫做分式,
其中A是分式的分子,B是分式的分母。
B中含有字母
分式
B中含有字母
分式
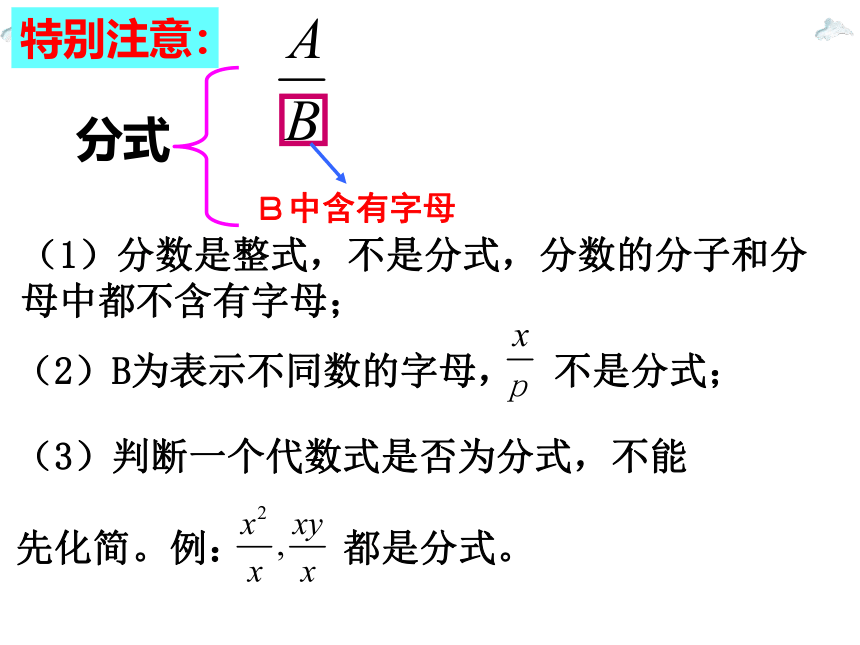
特别注意:
(2)B为表示不同数的字母, 不是分式;
(3)判断一个代数式是否为分式,不能
先化简。例: 都是分式。
(1)分数是整式,不是分式,分数的分子和分母中都不含有字母;
(2)
(3)
2a+b,
(4)
(5)
请判断下列各式是否为分式?若不是,请说明理由.
(1)
(6)
及时巩固
(3)(5)(6)是的;
(1)(2)(4)不是。
分式的值随分式中字母取值的变化而变化。
用具体的数值代替分式中的字母,按照式子中
的运算关系计算,就能得到相应的分式的值.
例1:求分式 的值:
(1) (2)a=
典例探究
解:(1)当a=3时,原式=
(2)当a= 时,原式=
例1:求分式 的值:
(1) (2)a=
典例探究
思考:在分式 中,a的值可以是-2吗?
为什么?
分式的分母不能为0.如果分式中字母所取的值使分母的值为0,那么分式无意义.
例2、当x取什么值时,分式
(1)无意义、有意义?
(2)分式的值为零?
典例探究
解:(1)由2x-3=0,得
当 时,原式无意义.
当 时,原式有意义.
例2、当x取什么值时,分式
(1)无意义、有意义?
(2)分式的值为零?
典例探究
解:(2)由 ,得x=2
当x=2时,原式的值为零.
分式 有无意义,何时为零
1、当B=0时,分式 无意义。
2、当B ≠0时,分式 有意义。
3.分式 中,当A=0且B≠0时,分式的值为零.
练习1:当x取什么值时,下列分式有意义:
(1) (2)
及时巩固
练习2:当x取任意实数时,下列分式中一定有意义的是( )
A. B.
C. D.
及时巩固
D
例3、当a= 时,分式 的值为零.
典例探究
变形:当a= 时,分式
的值为零.
4
2
练习:当x分别为何值时,下列分式的值为0?
及时巩固
练习:当x分别为何值时,下列分式的值为0?
练习:当x分别为何值时,下列分式的值为0?
分式可以表示现实生活中的一些数量关系.
例如:如果a(元)表示购买笔记本的钱数,b(元)表示每本笔记本的售价,那么 表示每本笔记降价1元后,用a元可购得笔记本的本数;
如果a表示长方形的面积,b表示长方形的宽,那么 表示宽减少1个单位长度后,面积为a的长方形的长.
例4、试解释分式 所表示的实际意义:
1、a取何整数时,分式
的值为正整数.
拓展提高
答:a=0、1、3.
解:由题意得:
a+1=1或2或4
∴a=0或1或3
拓展提高
变:a取何整数时,分式
的值为整数.
答:a=0、-2、1、-3、3、-5.
解:由题意得:
a+1= ± 1或± 2或± 4
∴a=0、-2、1、-3、3、-5
2.当x为何值时,分式 的值为正数?
拓展提高
解: ∵x2+1>0, 的值为正数
∴5-x>0
∴x<5
变:当x为何值时,分式 的值为负数?
拓展提高
解:由题意得:
或
∴无解或-1∴-13、(1)已知a、b满足a2+2ab+b2=0(b≠0),
求 的值;
拓展提高
解:∵a2+2ab+b2=0
∴(a+b)2=0
∴a+b=0
∵ b≠0
∴a=-b
∴ =-1
(2)已知x满足x2+x-1=0,求 的值;
3、
拓展提高
解:∵x2+x-1=0
∴x≠0
∴
∴ =-1
1、形如 ,并且B中含有字母的式子叫做分式其中B≠0.整式和分式统称为有理式.
2、分式 中:B≠0时,分式有意义;
分式 中:B=0时,分式无意义;
分式 中,当A=0且B≠0时,分式的值为零.
课堂小结
谢谢!
复习回顾:
单项式、多项式、整式:
说明:单独一个数或一个字母也是单项式.
3、单项式和多项式统称为整式.
1、数与字母乘积的代数式叫做单项式.
例:2,x,2x,2x2y2, ,...
2、几个单项式的和叫做多项式.
例:x+y,x2+y2+z3+1,πR2-πr2, 都是多项式
1、如果某市人口总数为a人,绿地面积为bm2 ,
那么该市人均拥有绿地 m2;
问题情境
2、如果一块长方形玻璃板的面积为2m2,这块玻璃板的宽为am,那么它的长是 m;
3、如果面积为a公顷、b公顷的两块棉田分别产棉花m千克、n千克,那么这两块棉田平均每公顷产棉花______千克.
讨论
像 、 、 …… 这样的式子有什么
共同特征?
它们与整式有什么区别?
一般地,如果A、B表示两个整式,
分式的定义
并且B中含有字母,
那么代数式
叫做分式,
其中A是分式的分子,B是分式的分母。
B中含有字母
分式
B中含有字母
分式
特别注意:
(2)B为表示不同数的字母, 不是分式;
(3)判断一个代数式是否为分式,不能
先化简。例: 都是分式。
(1)分数是整式,不是分式,分数的分子和分母中都不含有字母;
(2)
(3)
2a+b,
(4)
(5)
请判断下列各式是否为分式?若不是,请说明理由.
(1)
(6)
及时巩固
(3)(5)(6)是的;
(1)(2)(4)不是。
分式的值随分式中字母取值的变化而变化。
用具体的数值代替分式中的字母,按照式子中
的运算关系计算,就能得到相应的分式的值.
例1:求分式 的值:
(1) (2)a=
典例探究
解:(1)当a=3时,原式=
(2)当a= 时,原式=
例1:求分式 的值:
(1) (2)a=
典例探究
思考:在分式 中,a的值可以是-2吗?
为什么?
分式的分母不能为0.如果分式中字母所取的值使分母的值为0,那么分式无意义.
例2、当x取什么值时,分式
(1)无意义、有意义?
(2)分式的值为零?
典例探究
解:(1)由2x-3=0,得
当 时,原式无意义.
当 时,原式有意义.
例2、当x取什么值时,分式
(1)无意义、有意义?
(2)分式的值为零?
典例探究
解:(2)由 ,得x=2
当x=2时,原式的值为零.
分式 有无意义,何时为零
1、当B=0时,分式 无意义。
2、当B ≠0时,分式 有意义。
3.分式 中,当A=0且B≠0时,分式的值为零.
练习1:当x取什么值时,下列分式有意义:
(1) (2)
及时巩固
练习2:当x取任意实数时,下列分式中一定有意义的是( )
A. B.
C. D.
及时巩固
D
例3、当a= 时,分式 的值为零.
典例探究
变形:当a= 时,分式
的值为零.
4
2
练习:当x分别为何值时,下列分式的值为0?
及时巩固
练习:当x分别为何值时,下列分式的值为0?
练习:当x分别为何值时,下列分式的值为0?
分式可以表示现实生活中的一些数量关系.
例如:如果a(元)表示购买笔记本的钱数,b(元)表示每本笔记本的售价,那么 表示每本笔记降价1元后,用a元可购得笔记本的本数;
如果a表示长方形的面积,b表示长方形的宽,那么 表示宽减少1个单位长度后,面积为a的长方形的长.
例4、试解释分式 所表示的实际意义:
1、a取何整数时,分式
的值为正整数.
拓展提高
答:a=0、1、3.
解:由题意得:
a+1=1或2或4
∴a=0或1或3
拓展提高
变:a取何整数时,分式
的值为整数.
答:a=0、-2、1、-3、3、-5.
解:由题意得:
a+1= ± 1或± 2或± 4
∴a=0、-2、1、-3、3、-5
2.当x为何值时,分式 的值为正数?
拓展提高
解: ∵x2+1>0, 的值为正数
∴5-x>0
∴x<5
变:当x为何值时,分式 的值为负数?
拓展提高
解:由题意得:
或
∴无解或-1
求 的值;
拓展提高
解:∵a2+2ab+b2=0
∴(a+b)2=0
∴a+b=0
∵ b≠0
∴a=-b
∴ =-1
(2)已知x满足x2+x-1=0,求 的值;
3、
拓展提高
解:∵x2+x-1=0
∴x≠0
∴
∴ =-1
1、形如 ,并且B中含有字母的式子叫做分式其中B≠0.整式和分式统称为有理式.
2、分式 中:B≠0时,分式有意义;
分式 中:B=0时,分式无意义;
分式 中,当A=0且B≠0时,分式的值为零.
课堂小结
谢谢!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
