苏科版数学七年级下册 7.2 探索平行线的性质 课件 (共29张PPT)
文档属性
| 名称 | 苏科版数学七年级下册 7.2 探索平行线的性质 课件 (共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 667.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览


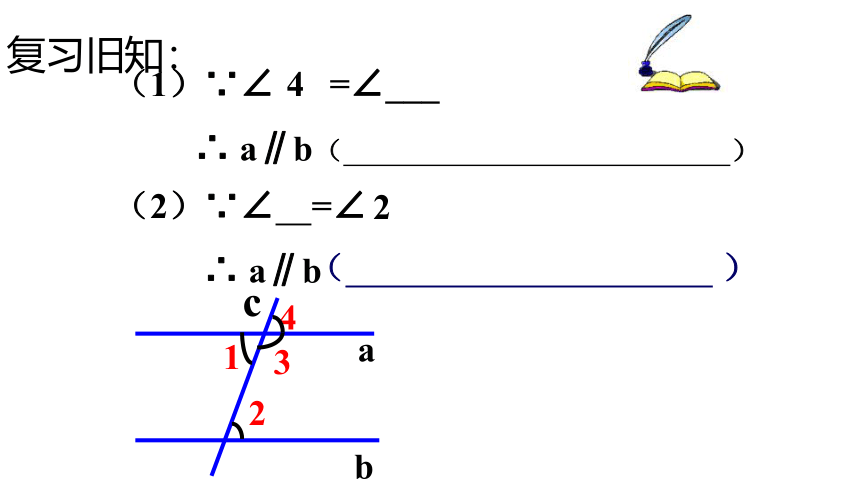
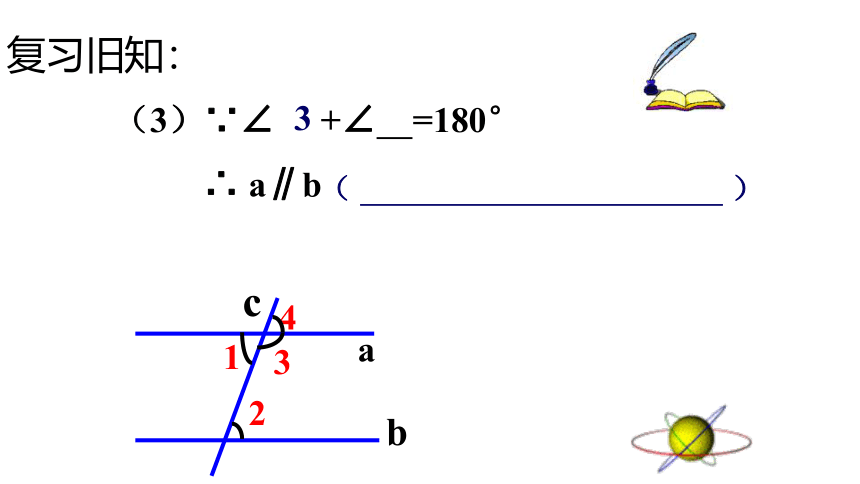

文档简介
7.探索平行线的性质
数学不是看出来的,也不是想出来的,而是做出来的。
学习目标:
经历操作、度量、观察、思考等过程,探究、发现平行线的性质,能应用平行线的性质及判定方法解决相关问题。
( )
(1)∵∠ =∠___
∴ a∥b
( )
(2)∵∠ =∠
∴ a∥b
2
4
c
b
4
3
2
1
a
复习旧知:
( )
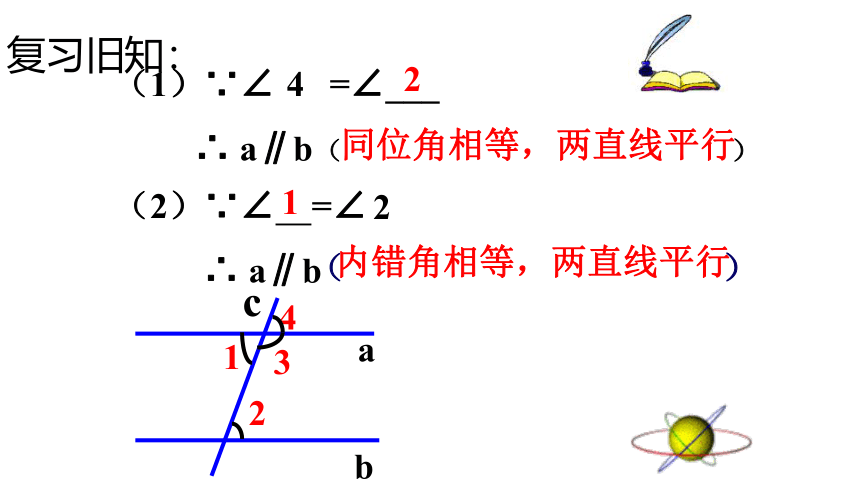
(1)∵∠ =∠___
∴ a∥b
( )
(2)∵∠ =∠
∴ a∥b
1
2
2
4
同位角相等,两直线平行
内错角相等,两直线平行
c
b
4
3
2
1
a
复习旧知:
( )
(3)∵∠ +∠ =180°
∴ a∥b
3
4
3
2
1
a
c
b
复习旧知:
( )
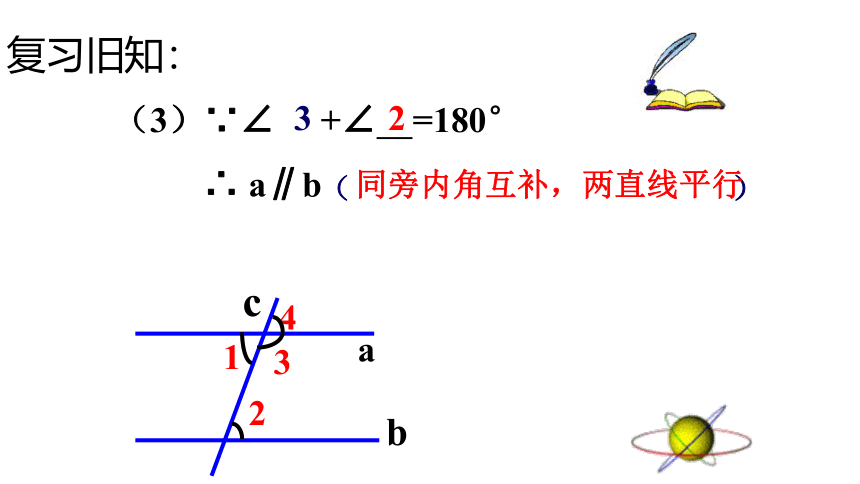
(3)∵∠ +∠ =180°
∴ a∥b
2
3
同旁内角互补,两直线平行
4
3
2
1
a
c
b
复习旧知:
A
B
C
D
M
N
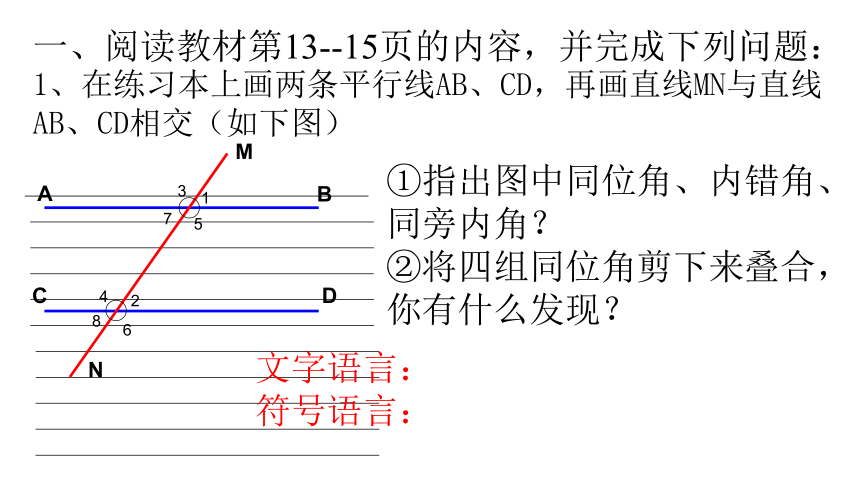
1、在练习本上画两条平行线AB、CD,再画直线MN与直线AB、CD相交(如下图)
①指出图中同位角、内错角、
同旁内角?
②将四组同位角剪下来叠合,
你有什么发现?
7
5
1
2
3
4
6
8
一、阅读教材第13--15页的内容,并完成下列问题:
文字语言:
符号语言:
A
B
C
D
M
N
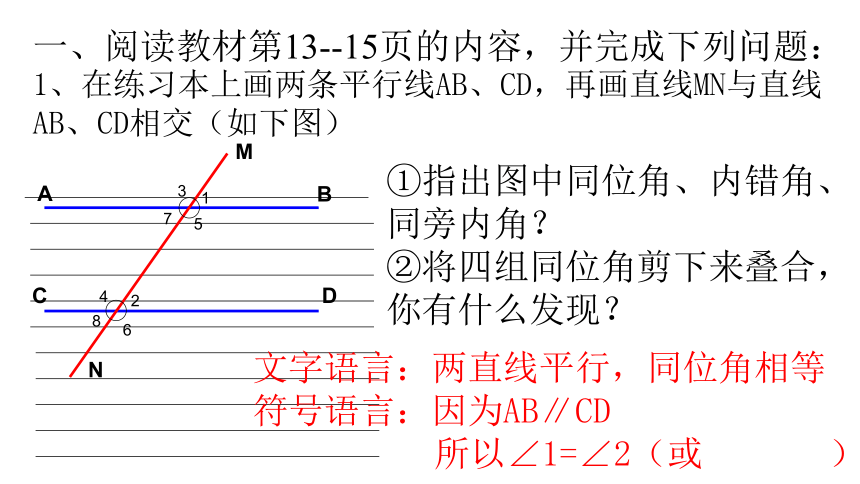
1、在练习本上画两条平行线AB、CD,再画直线MN与直线AB、CD相交(如下图)
①指出图中同位角、内错角、
同旁内角?
②将四组同位角剪下来叠合,
你有什么发现?
7
5
1
2
3
4
6
8
一、阅读教材第13--15页的内容,并完成下列问题:
文字语言:两直线平行,同位角相等
符号语言:因为AB∥CD
所以∠1=∠2(或 )
一、阅读教材第13--15页的内容,并完成下列问题:
2、如果我们现在只知道”两直线平行,同位角相等”.你能说明“两直线平行,内错角相等”吗?
已知:a∥b,求:∠2=∠3
解:.....
a
b
c
1
2
3
总结:文字语言:
两直线平行,内错角 ;
符号语言:
一、阅读教材第13--15页的内容,并完成下列问题:
2、如果我们现在只知道”两直线平行,同位角相等”.你能说明“两直线平行,内错角相等”吗?
解:如图∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
又∵ ∠1=∠3(对顶角相等)
∴ ∠2=∠3(等量代换)
a
b
c
1
2
3
总结:文字语言:
两直线平行,内错角 ;
相等
符号语言:因为a∥b
所以∠2=∠3
解:
1
a
3
2
b
.........
一、阅读教材第13--15页的内容,并完成下列问题:
2、如果我们现在只知道”两直线平行,同位角相等”.你能说明“两直线平行,同旁内角互补”吗?
总结:文字语言:
两直线平行,同旁内角 ;
符号语言:
已知:a∥b,求:∠2+∠3=180°
∴ ∠2 + ∠3 = 180°
解:
1
a
3
2
b
∵a∥b
(已知)
∴∠1=∠2
(两直线平行,
同位角相等)
又∵ ∠1+∠3 = 180°
(平角定义)
(等量代换)
一、阅读教材第13--15页的内容,并完成下列问题:
2、如果我们现在只知道”两直线平行,同位角相等”.你能说明“两直线平行,同旁内角互补”吗?
总结:文字语言:
两直线平行,同旁内角 ;
互补
符号语言:因为a∥b
所以∠2+∠3=180°
例1 已知:直线a∥b,c∥d, ∠1=115°,求∠2与∠3的度数
解:.......
判定
同位角相等两直线平行
性质
两直线平行同位角相等
1
2
3
a
b
c
d
二、典型例题:
例1 已知:直线a∥b,c∥d, ∠1=115°,求∠2与∠3的度数
解:
∵ a∥b
∴∠2=∠1=115°
∵ c∥d
∴∠3=∠2=115°
(两直线平行,内错角相等)
(已知)
(已知)
(两直线平行,同位角相等)
1
2
3
a
b
c
d
二、典型例题:
A
B
C
E
2
1
例2 如图:点B、C、D在一条直线上,AB∥EC,∠A=55°,
∠B=60°.求∠1、∠2和∠ACB的度数。
解:........
二、典型例题:
D
A
B
C
E
2
1
例2 如图:点B、C、D在一条直线上,AB∥EC,∠A=55°,
∠B=60°.求∠1、∠2和∠ACB的度数。
解:因为AB∥CE,且∠A=55°
根据“两直线平行,内错角相等”
所以∠A=∠1=55°.
因为AB∥CE,∠B=60°
根据“两直线平行,同位角相等” 所以∠ACB=180°-
所以∠B=∠2=60°. ∠1- ∠2
又因为点B、C、D在一条直线上 =180°-55°-60°
所以 ∠ 1+∠2+∠ACB=180° =65°
二、典型例题:
D
二、典型例题:
例3 如图,AB∥DC,BC∥DE,试说明∠B+∠D=180°请完成下面的推理过程
解:因为BC∥DE( )
所以∠C= ;
( )
又因为 ;
所以∠B+∠C=180°
( )
所以∠B+∠D=180°
( )
二、典型例题:
例3 如图,AB∥DC,BC∥DE,试说明∠B+∠D=180°请完成下面的推理过程
解:因为BC∥DE( )
所以∠C= ;
( )
又因为 ;
所以∠B+∠C=180°
( )
所以∠B+∠D=180°
( )
已知
∠D
两直线平行内错角相等
AB∥CD
两直线平行同旁内角互补
等量代换
1.如图若AB ∥ CD,则下列结论中
① ∠B=∠2 ② ∠3=∠A ③ ∠3=∠B
④ ∠B + ∠BCD= 180° 正确的是 ( )
A ① ② B ① ③
C ① ④ D ③ ④
A
B
E
C
D
1
2
3
三、例题巩固:
1.如图若AB ∥ CD,则下列结论中
① ∠B=∠2 ② ∠3=∠A ③ ∠3=∠B
④ ∠B + ∠BCD= 180° 正确的是 ( )
A ① ② B ① ③
C ① ④ D ③ ④
D
A
B
E
C
D
1
2
3
×
√
×
√
三、例题巩固:
2.如图,若AB ∥ ED,BC ∥ FE,
则∠B + ∠E=_______
A
B
C
D
E
F
三、例题巩固:
2.如图,若AB ∥ ED,BC ∥ FE,
则∠B + ∠E=_______
A
B
C
D
E
F
180°
三、例题巩固:
复习:
两直线平行的判定:
同位角相等,两直线平行
内错角相等两直线平行
同旁内角互补两直线平行
两直线平行的性质:
两直线平行,同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
条件: 结论: ;
条件: 结论: ;
3、已知 DE∥BC,∠1=∠2,∠D:∠DBC=2:1, 求∠3的度数.
D
E
B
C
2
1
3
解:...... M N
3、已知DE∥BC,∠1=∠2,∠D:∠DBC=2:1, 求∠3的度数.
D
E
B
C
2
1
3
解:因为DE∥BC(已知)
所以∠D+∠DBC=180°∠1=∠3
(两直线平行同旁内角互补
两直线平行内错角相等)
又因为∠D:∠DBC=2:1 (已知)
所以∠DBC=60°
又因为∠1=∠2(已知)
所以∠1=30°(角平分线定义)
所以∠3=30°(等量代换)
四、拓展延伸:
1、如图,AB∥DE,∠A=150°,∠D=140°,则∠C的度数
( )
A.50° B.60° C.70° D.75°
提示:过点C作AB的平行线CF
四、拓展延伸:
1、如图,AB∥DE,∠A=150°,∠D=140°,则∠C的度数
( )
A.50° B.60° C.70° D.75°
提示:过点C作AB的平行线CF
-----------------F
四、拓展延伸:
2、如图,AB∥CD,点E、G分别在AB、CD上,且∠AEG=34°,EF⊥EG,交CD于点F。求∠EFG的度数。
特殊时期,同学们加油。
数学不是看出来的,也不是想出来的,而是做出来的。
学习目标:
经历操作、度量、观察、思考等过程,探究、发现平行线的性质,能应用平行线的性质及判定方法解决相关问题。
( )
(1)∵∠ =∠___
∴ a∥b
( )
(2)∵∠ =∠
∴ a∥b
2
4
c
b
4
3
2
1
a
复习旧知:
( )
(1)∵∠ =∠___
∴ a∥b
( )
(2)∵∠ =∠
∴ a∥b
1
2
2
4
同位角相等,两直线平行
内错角相等,两直线平行
c
b
4
3
2
1
a
复习旧知:
( )
(3)∵∠ +∠ =180°
∴ a∥b
3
4
3
2
1
a
c
b
复习旧知:
( )
(3)∵∠ +∠ =180°
∴ a∥b
2
3
同旁内角互补,两直线平行
4
3
2
1
a
c
b
复习旧知:
A
B
C
D
M
N
1、在练习本上画两条平行线AB、CD,再画直线MN与直线AB、CD相交(如下图)
①指出图中同位角、内错角、
同旁内角?
②将四组同位角剪下来叠合,
你有什么发现?
7
5
1
2
3
4
6
8
一、阅读教材第13--15页的内容,并完成下列问题:
文字语言:
符号语言:
A
B
C
D
M
N
1、在练习本上画两条平行线AB、CD,再画直线MN与直线AB、CD相交(如下图)
①指出图中同位角、内错角、
同旁内角?
②将四组同位角剪下来叠合,
你有什么发现?
7
5
1
2
3
4
6
8
一、阅读教材第13--15页的内容,并完成下列问题:
文字语言:两直线平行,同位角相等
符号语言:因为AB∥CD
所以∠1=∠2(或 )
一、阅读教材第13--15页的内容,并完成下列问题:
2、如果我们现在只知道”两直线平行,同位角相等”.你能说明“两直线平行,内错角相等”吗?
已知:a∥b,求:∠2=∠3
解:.....
a
b
c
1
2
3
总结:文字语言:
两直线平行,内错角 ;
符号语言:
一、阅读教材第13--15页的内容,并完成下列问题:
2、如果我们现在只知道”两直线平行,同位角相等”.你能说明“两直线平行,内错角相等”吗?
解:如图∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
又∵ ∠1=∠3(对顶角相等)
∴ ∠2=∠3(等量代换)
a
b
c
1
2
3
总结:文字语言:
两直线平行,内错角 ;
相等
符号语言:因为a∥b
所以∠2=∠3
解:
1
a
3
2
b
.........
一、阅读教材第13--15页的内容,并完成下列问题:
2、如果我们现在只知道”两直线平行,同位角相等”.你能说明“两直线平行,同旁内角互补”吗?
总结:文字语言:
两直线平行,同旁内角 ;
符号语言:
已知:a∥b,求:∠2+∠3=180°
∴ ∠2 + ∠3 = 180°
解:
1
a
3
2
b
∵a∥b
(已知)
∴∠1=∠2
(两直线平行,
同位角相等)
又∵ ∠1+∠3 = 180°
(平角定义)
(等量代换)
一、阅读教材第13--15页的内容,并完成下列问题:
2、如果我们现在只知道”两直线平行,同位角相等”.你能说明“两直线平行,同旁内角互补”吗?
总结:文字语言:
两直线平行,同旁内角 ;
互补
符号语言:因为a∥b
所以∠2+∠3=180°
例1 已知:直线a∥b,c∥d, ∠1=115°,求∠2与∠3的度数
解:.......
判定
同位角相等两直线平行
性质
两直线平行同位角相等
1
2
3
a
b
c
d
二、典型例题:
例1 已知:直线a∥b,c∥d, ∠1=115°,求∠2与∠3的度数
解:
∵ a∥b
∴∠2=∠1=115°
∵ c∥d
∴∠3=∠2=115°
(两直线平行,内错角相等)
(已知)
(已知)
(两直线平行,同位角相等)
1
2
3
a
b
c
d
二、典型例题:
A
B
C
E
2
1
例2 如图:点B、C、D在一条直线上,AB∥EC,∠A=55°,
∠B=60°.求∠1、∠2和∠ACB的度数。
解:........
二、典型例题:
D
A
B
C
E
2
1
例2 如图:点B、C、D在一条直线上,AB∥EC,∠A=55°,
∠B=60°.求∠1、∠2和∠ACB的度数。
解:因为AB∥CE,且∠A=55°
根据“两直线平行,内错角相等”
所以∠A=∠1=55°.
因为AB∥CE,∠B=60°
根据“两直线平行,同位角相等” 所以∠ACB=180°-
所以∠B=∠2=60°. ∠1- ∠2
又因为点B、C、D在一条直线上 =180°-55°-60°
所以 ∠ 1+∠2+∠ACB=180° =65°
二、典型例题:
D
二、典型例题:
例3 如图,AB∥DC,BC∥DE,试说明∠B+∠D=180°请完成下面的推理过程
解:因为BC∥DE( )
所以∠C= ;
( )
又因为 ;
所以∠B+∠C=180°
( )
所以∠B+∠D=180°
( )
二、典型例题:
例3 如图,AB∥DC,BC∥DE,试说明∠B+∠D=180°请完成下面的推理过程
解:因为BC∥DE( )
所以∠C= ;
( )
又因为 ;
所以∠B+∠C=180°
( )
所以∠B+∠D=180°
( )
已知
∠D
两直线平行内错角相等
AB∥CD
两直线平行同旁内角互补
等量代换
1.如图若AB ∥ CD,则下列结论中
① ∠B=∠2 ② ∠3=∠A ③ ∠3=∠B
④ ∠B + ∠BCD= 180° 正确的是 ( )
A ① ② B ① ③
C ① ④ D ③ ④
A
B
E
C
D
1
2
3
三、例题巩固:
1.如图若AB ∥ CD,则下列结论中
① ∠B=∠2 ② ∠3=∠A ③ ∠3=∠B
④ ∠B + ∠BCD= 180° 正确的是 ( )
A ① ② B ① ③
C ① ④ D ③ ④
D
A
B
E
C
D
1
2
3
×
√
×
√
三、例题巩固:
2.如图,若AB ∥ ED,BC ∥ FE,
则∠B + ∠E=_______
A
B
C
D
E
F
三、例题巩固:
2.如图,若AB ∥ ED,BC ∥ FE,
则∠B + ∠E=_______
A
B
C
D
E
F
180°
三、例题巩固:
复习:
两直线平行的判定:
同位角相等,两直线平行
内错角相等两直线平行
同旁内角互补两直线平行
两直线平行的性质:
两直线平行,同位角相等
两直线平行内错角相等
两直线平行同旁内角互补
条件: 结论: ;
条件: 结论: ;
3、已知 DE∥BC,∠1=∠2,∠D:∠DBC=2:1, 求∠3的度数.
D
E
B
C
2
1
3
解:...... M N
3、已知DE∥BC,∠1=∠2,∠D:∠DBC=2:1, 求∠3的度数.
D
E
B
C
2
1
3
解:因为DE∥BC(已知)
所以∠D+∠DBC=180°∠1=∠3
(两直线平行同旁内角互补
两直线平行内错角相等)
又因为∠D:∠DBC=2:1 (已知)
所以∠DBC=60°
又因为∠1=∠2(已知)
所以∠1=30°(角平分线定义)
所以∠3=30°(等量代换)
四、拓展延伸:
1、如图,AB∥DE,∠A=150°,∠D=140°,则∠C的度数
( )
A.50° B.60° C.70° D.75°
提示:过点C作AB的平行线CF
四、拓展延伸:
1、如图,AB∥DE,∠A=150°,∠D=140°,则∠C的度数
( )
A.50° B.60° C.70° D.75°
提示:过点C作AB的平行线CF
-----------------F
四、拓展延伸:
2、如图,AB∥CD,点E、G分别在AB、CD上,且∠AEG=34°,EF⊥EG,交CD于点F。求∠EFG的度数。
特殊时期,同学们加油。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
