苏科版数学七年级下册7.1探索直线平行的条件(1)课件(17张PPT)
文档属性
| 名称 | 苏科版数学七年级下册7.1探索直线平行的条件(1)课件(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 628.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览



文档简介
第7章 平面图形的认识(二)
7.1探索直线平行的条件(1)
七年级数学
一. 知识准备
完成下列各题:【2 min】
1.同一平面内两直线的位置关系有 与 ______两种 .
2.在同一平面内,_______的两条直线叫作平行线.
3.基本事实: 过_______一点有且只有___条直线与这条直线平行.
4.如图,点A为直线 外任意一点,过点A作一条直线 ,使
.
七年级数学
不相交
相交
平行
直线外
一
A
七年级数学
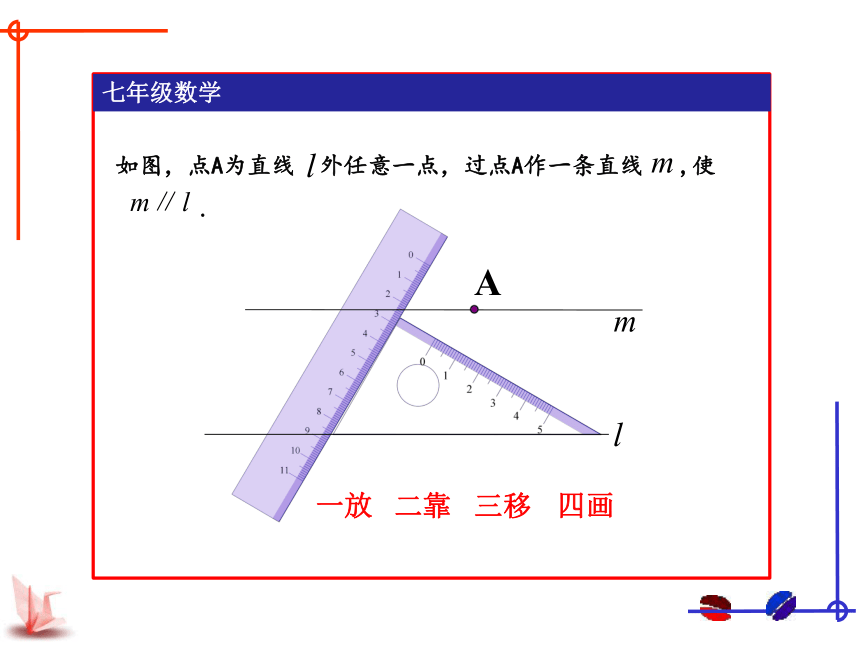
如图,点A为直线 外任意一点,过点A作一条直线 ,使
.
A
一放
二靠
三移
四画
七年级数学
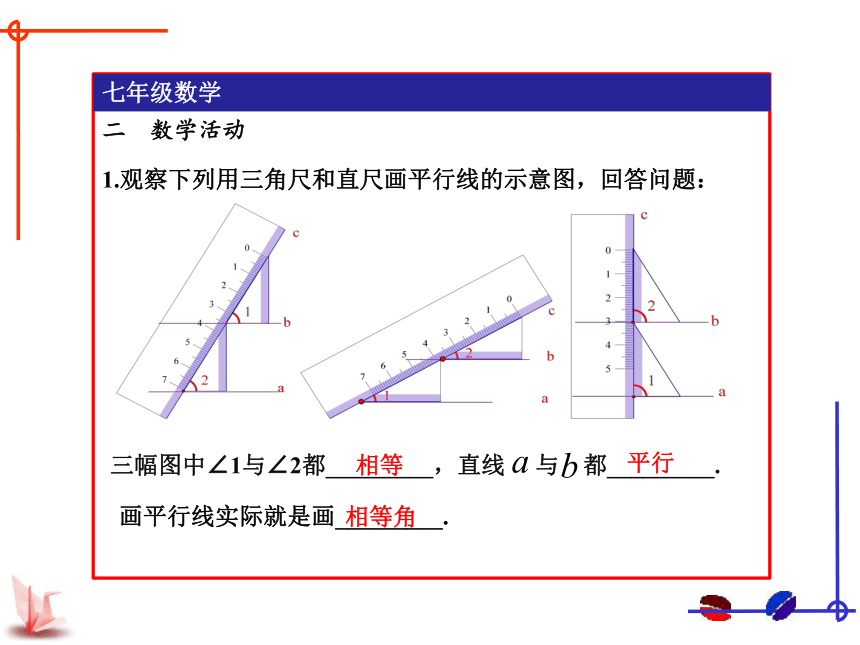
1.观察下列用三角尺和直尺画平行线的示意图,回答问题:
二 数学活动
三幅图中∠1与∠2都_________,直线 与 都_________.
画平行线实际就是画_________.
相等
平行
相等角
七年级数学
2.如图,三根木条相交成∠1, ∠2,固定木条b、c,绕固定点A转动木条a .观察操作并完成填空:
平行
不平行
过直线外一点有且只有一条直线与这条直线平行
A
(1)当∠2与∠1相等时,直线 与
_________ ;(2)当∠2与∠1不相等
时,直线 与 ___________;
(3)经过点A与直线 平行的直线
有___条,这是因为_____________________________________________.
一
∠1与∠2是否相等决定了直线 与 是否平行.
三 揭示概念
七年级数学
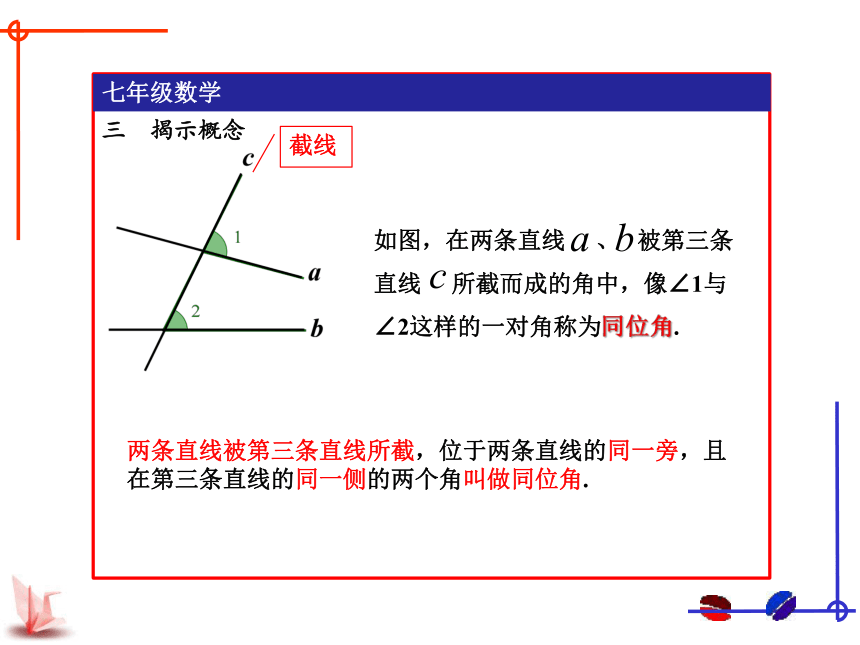
如图,在两条直线 、 被第三条直线 所截而成的角中,像∠1与∠2这样的一对角称为同位角.
截线
两条直线被第三条直线所截,位于两条直线的同一旁,且在第三条直线的同一侧的两个角叫做同位角.
七年级数学
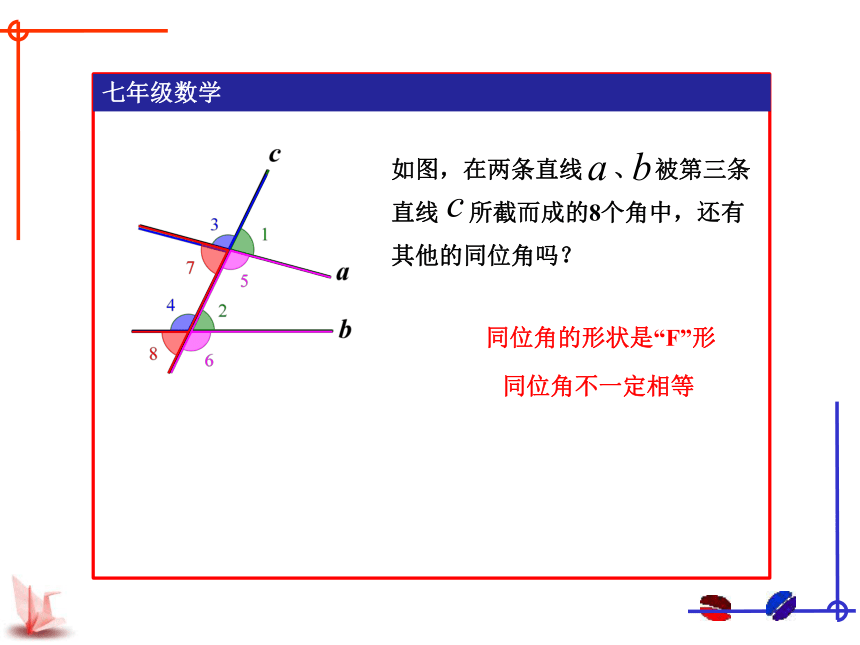
如图,在两条直线 、 被第三条直线 所截而成的8个角中,还有其他的同位角吗?
同位角的形状是“F”形
同位角不一定相等
七年级数学
四 概念辨析
1.下图中∠1和∠2是同位角吗?为什么?【2min】
∠1和∠2不是同位角
∠1和∠2是同位角
因为∠1和∠2无一边
共线.
因为∠1和∠2都在直线a、c
的右侧,且都在直线b的上方.
七年级数学
2.如图,∠1和∠2是同位角的有______________.(填序号)【2min】
(1)、(2)、(5)
七年级数学
3.根据右图完成填空.
(1)∠1和∠C是直线_____、_____被直线_____截成的同位角.
(2)∠2和∠B是直线_____、_____被直线_____截成的同位角.
(3)∠3和∠___是直线_____、_____被直线_____截成的同位角.
DE
BC
AC
DE
BC
AB
DF
C
AC
BC
五 归纳整理
七年级数学
∠1和∠2都是___________;
当∠1=∠2时,__________;
当∠1≠∠2时,_______________.
同位角
a∥b
a与b不平行
七年级数学
基本事实:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成: 同位角相等,两直线平行.
因为 ∠1=∠2
所以 AB∥CD
(同位角相等,两直线平行)
七年级数学
六 例题学习
例1 如图,∠1=∠C,∠2=∠C,指出图中互相平行的直线,并说明理由.【4min】
解:
AB∥CD,AC∥BD
因为∠1=∠C
所以AB∥CD
(同位角相等,两直线平行)
因为∠2=∠C
所以AC∥BD
(同位角相等,两直线平行)
七年级数学
例2 已知直线AB、CD被EF所截,∠1=∠2,如果∠BMN=∠DNF,那么MQ∥NP吗?为什么?
解:
MQ∥NP
因为∠1=∠2,∠BMN=∠DNF
所以∠1+∠BMN=∠2+∠DNF
(等式性质)
即∠QMN=∠PNF
所以MQ∥NP
(同位角相等,两直线平行)
七 小结思考
七年级数学
1.如何判断同位角?
两条直线被第三条直线所截,位于两条直线的同一旁,且在第三条直线的同一侧的两个角叫做同位角.
同位角是“F”形
2.判断两条直线平行的方法.
同位角不一定相等
①找出同位角;
②同位角相等.
因为 ∠1=∠2
所以 AB∥CD
(同位角相等,两直线平行)
七年级数学
1.如图,∠1的同位角有( )个.
A.1 B.2 C.3 D.4
2.如图.
(1)因为∠1和∠2是直线______和_____被直线____所截而成的________,且∠1=∠2,所以_______∥________;
(2)因为∠1和∠3是直线______和_____被直线____所截而成的________,且∠1 = ∠3,所以______∥______.
八 课堂检测【10min】
B
AB
CD
EF
同位角
AB
CD
EF
GH
AB
EF
同位角
GH
七年级数学
3 .已知直线AB、CD被EF所截,∠1=∠2,如果∠BME=∠DNM,那么MQ∥NP吗?为什么?
解:
MQ∥NP
因为∠1=∠2,∠BME=∠DNM
所以∠BME-∠1=∠DNM-∠2
(等式性质)
即∠QME=∠PNM
所以MQ∥NP
(同位角相等,两直线平行)
7.1探索直线平行的条件(1)
七年级数学
一. 知识准备
完成下列各题:【2 min】
1.同一平面内两直线的位置关系有 与 ______两种 .
2.在同一平面内,_______的两条直线叫作平行线.
3.基本事实: 过_______一点有且只有___条直线与这条直线平行.
4.如图,点A为直线 外任意一点,过点A作一条直线 ,使
.
七年级数学
不相交
相交
平行
直线外
一
A
七年级数学
如图,点A为直线 外任意一点,过点A作一条直线 ,使
.
A
一放
二靠
三移
四画
七年级数学
1.观察下列用三角尺和直尺画平行线的示意图,回答问题:
二 数学活动
三幅图中∠1与∠2都_________,直线 与 都_________.
画平行线实际就是画_________.
相等
平行
相等角
七年级数学
2.如图,三根木条相交成∠1, ∠2,固定木条b、c,绕固定点A转动木条a .观察操作并完成填空:
平行
不平行
过直线外一点有且只有一条直线与这条直线平行
A
(1)当∠2与∠1相等时,直线 与
_________ ;(2)当∠2与∠1不相等
时,直线 与 ___________;
(3)经过点A与直线 平行的直线
有___条,这是因为_____________________________________________.
一
∠1与∠2是否相等决定了直线 与 是否平行.
三 揭示概念
七年级数学
如图,在两条直线 、 被第三条直线 所截而成的角中,像∠1与∠2这样的一对角称为同位角.
截线
两条直线被第三条直线所截,位于两条直线的同一旁,且在第三条直线的同一侧的两个角叫做同位角.
七年级数学
如图,在两条直线 、 被第三条直线 所截而成的8个角中,还有其他的同位角吗?
同位角的形状是“F”形
同位角不一定相等
七年级数学
四 概念辨析
1.下图中∠1和∠2是同位角吗?为什么?【2min】
∠1和∠2不是同位角
∠1和∠2是同位角
因为∠1和∠2无一边
共线.
因为∠1和∠2都在直线a、c
的右侧,且都在直线b的上方.
七年级数学
2.如图,∠1和∠2是同位角的有______________.(填序号)【2min】
(1)、(2)、(5)
七年级数学
3.根据右图完成填空.
(1)∠1和∠C是直线_____、_____被直线_____截成的同位角.
(2)∠2和∠B是直线_____、_____被直线_____截成的同位角.
(3)∠3和∠___是直线_____、_____被直线_____截成的同位角.
DE
BC
AC
DE
BC
AB
DF
C
AC
BC
五 归纳整理
七年级数学
∠1和∠2都是___________;
当∠1=∠2时,__________;
当∠1≠∠2时,_______________.
同位角
a∥b
a与b不平行
七年级数学
基本事实:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成: 同位角相等,两直线平行.
因为 ∠1=∠2
所以 AB∥CD
(同位角相等,两直线平行)
七年级数学
六 例题学习
例1 如图,∠1=∠C,∠2=∠C,指出图中互相平行的直线,并说明理由.【4min】
解:
AB∥CD,AC∥BD
因为∠1=∠C
所以AB∥CD
(同位角相等,两直线平行)
因为∠2=∠C
所以AC∥BD
(同位角相等,两直线平行)
七年级数学
例2 已知直线AB、CD被EF所截,∠1=∠2,如果∠BMN=∠DNF,那么MQ∥NP吗?为什么?
解:
MQ∥NP
因为∠1=∠2,∠BMN=∠DNF
所以∠1+∠BMN=∠2+∠DNF
(等式性质)
即∠QMN=∠PNF
所以MQ∥NP
(同位角相等,两直线平行)
七 小结思考
七年级数学
1.如何判断同位角?
两条直线被第三条直线所截,位于两条直线的同一旁,且在第三条直线的同一侧的两个角叫做同位角.
同位角是“F”形
2.判断两条直线平行的方法.
同位角不一定相等
①找出同位角;
②同位角相等.
因为 ∠1=∠2
所以 AB∥CD
(同位角相等,两直线平行)
七年级数学
1.如图,∠1的同位角有( )个.
A.1 B.2 C.3 D.4
2.如图.
(1)因为∠1和∠2是直线______和_____被直线____所截而成的________,且∠1=∠2,所以_______∥________;
(2)因为∠1和∠3是直线______和_____被直线____所截而成的________,且∠1 = ∠3,所以______∥______.
八 课堂检测【10min】
B
AB
CD
EF
同位角
AB
CD
EF
GH
AB
EF
同位角
GH
七年级数学
3 .已知直线AB、CD被EF所截,∠1=∠2,如果∠BME=∠DNM,那么MQ∥NP吗?为什么?
解:
MQ∥NP
因为∠1=∠2,∠BME=∠DNM
所以∠BME-∠1=∠DNM-∠2
(等式性质)
即∠QME=∠PNM
所以MQ∥NP
(同位角相等,两直线平行)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
