苏科版数学七年级下册 7.3 图形的平移 课件 (共20张PPT)
文档属性
| 名称 | 苏科版数学七年级下册 7.3 图形的平移 课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 940.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览





文档简介
7.3图形的平移
数学不是看出来的,也不是想出来的,而是做出来的。
学习目标:
经历探索平移的基本性质的过程,能利用平移设计图案,发展空间观念。增强审美意识。
复习旧知:
1.图形变换的三种基本方式是: 。
平移,翻折,旋转
2.通过这三种变换只改变原图形的 ,
不改变原图形的 和 。
位置
形状 大小
1.手扶电梯上的人、笔直轨道上的列车…都在沿着某一方向移动,如果将生活问题数学化,它们都是图形变化中的 。
2.定义:在平面内,将一个图形沿着 移动
,这样的图形运动叫做图形的平移。
一、阅读教材第18--21页的内容,并完成下列问题:
平移
某个方向
一定的距离
3.平移的要素: 与 。
平移的方向 平移的距离
4.把三角形ABC 向右平行移动6格,画出所得到的三角形A′B′C′.
(1)度量三角形ABC与三角形A′B′C′的边、角的大小,你发现了什么?
A
B
C
度量得:
边: ,
,
,
角: ,
,
.
一、阅读教材第18--21页的内容,并完成下列问题:
AB=A′B′ BC=B′C′ AC=A′C′
∠A=∠A′
∠B=∠B′ ∠C=∠C′
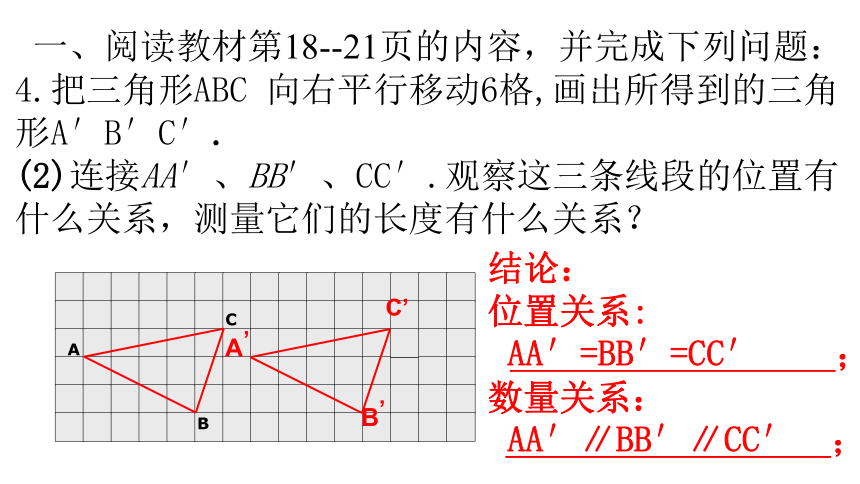
4.把三角形ABC 向右平行移动6格,画出所得到的三角形A′B′C′.
(2)连接AA′、BB′、CC′.观察这三条线段的位置有什么关系,测量它们的长度有什么关系?
A
B
C
一、阅读教材第18--21页的内容,并完成下列问题:
A’
B’
C’
结论:
位置关系:
;
数量关系:
;
AA′=BB′=CC′
AA′∥BB′∥CC′
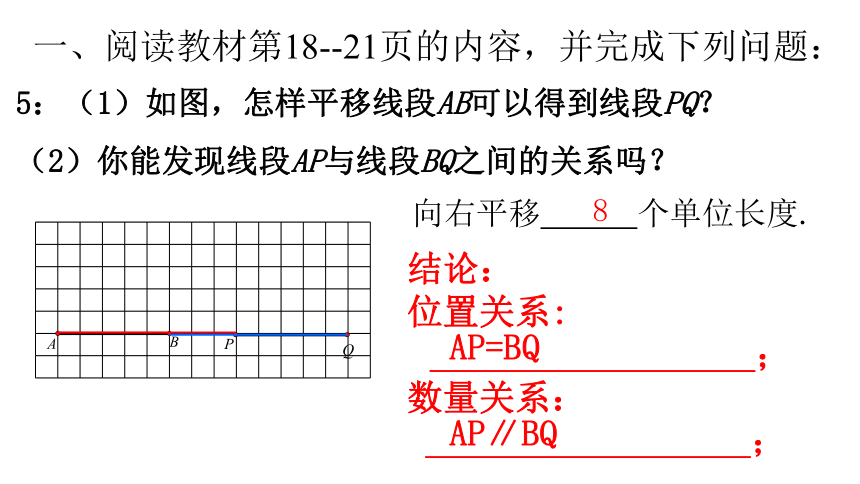
5:(1)如图,怎样平移线段AB可以得到线段PQ?
(2)你能发现线段AP与线段BQ之间的关系吗?
P
B
A
Q
一、阅读教材第18--21页的内容,并完成下列问题:
8
向右平移 个单位长度.
结论:
位置关系:
;
数量关系:
;
AP=BQ
AP∥BQ
一、阅读教材第18--21页的内容,并完成下列问题:
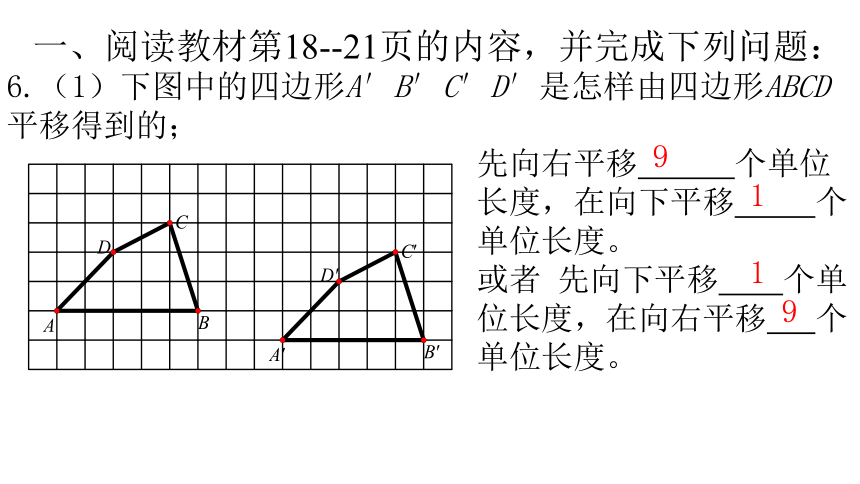
6.(1)下图中的四边形A′B′C′D′是怎样由四边形ABCD平移得到的;
先向右平移 个单位长度,在向下平移 个单位长度。
或者 先向下平移 个单位长度,在向右平移 个单位长度。
9
1
1
9
一、阅读教材第18--21页的内容,并完成下列问题:
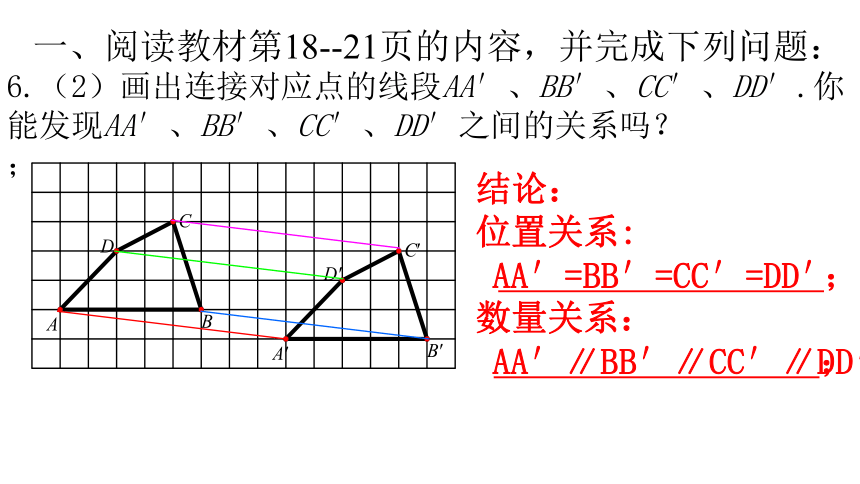
6.(2)画出连接对应点的线段AA′、BB′、CC′、DD′.你能发现AA′、BB′、CC′、DD′之间的关系吗?
;
结论:
位置关系:
;
数量关系:
;
AA′=BB′=CC′=DD′
AA′∥BB′∥CC′∥DD′
一、阅读教材第18--21页的内容,并完成下列问题:
6.(3)取线段AD的中点M,画出点M平移后对应的点M′.连接MM′.线段MM′与线段AA′有什么关系?
;
结论:
位置关系:
;
数量关系:
;
AA′=MM′
AA′∥MM′
M
M ′
A
B
P
Q
一、阅读教材第18--21页的内容,并完成下列问题:
一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等.
7.平移的性质:
。
例1.平移三角形ABC,使顶点A移到点D的位置. 画出平移后得到的三角形.
注意:对应点的连线用虚线,用圆规截取相等的相等的线段。保留作图痕迹。
D
C
B
A
二、典型例题:
1.在下面的六幅图案中,(2)、(3)、(4)、(5)、(6)中的哪个图案可以通过平移图案(1)得到?( )
3
三、例题巩固:
2.将A图案剪成若干小块,再分别平移后能够得到B、C、D中的 ( )
A.0个 B.1个 C.2个 D.3个
三、例题巩固:
C
3.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则下列结论正确的是( )
A. FG=5,∠G=70°
B. EH=5,∠F=70°
C. EF=5,∠F=70°
D. EF=5,∠E=70°
H
G
F
E
D
C
B
A
B
三、例题巩固:
8
m
3
m
4.楼梯的高度3米,水平宽度8米,现要在楼梯的表面铺地毯,地毯每米16元,求购买地毯至少需花多少钱?
B A
E
C D
F
三、例题巩固:
5.将∠ABC向上平移10cm得到∠EFG,如果∠ABC=52°,则∠EFG= °,BF= cm。
10cm
52
B
C
A
F
E
G
O
三、例题巩固:
52° 10
四、拓展延伸:
1.如图,半径为2cm的半圆向右平移5cm所扫过的阴影部分面积为 cm2。
20
2.如图,将△ABC 沿着从A到D的方向平移后得到△DEF,若AB=4cm,BE=3cm,CE=1cm.
(1)指出平移的距离是多少?
(2)求线段BF的长.
F
E
D
C
B
A
四、拓展延伸:
3.如图,将△ABC沿边BC方向向右平移2cm,得到△DEF,则四边形ABFD的周长为20cm,则△ABC的周长为 。
16
四、拓展延伸:
数学不是看出来的,也不是想出来的,而是做出来的。
学习目标:
经历探索平移的基本性质的过程,能利用平移设计图案,发展空间观念。增强审美意识。
复习旧知:
1.图形变换的三种基本方式是: 。
平移,翻折,旋转
2.通过这三种变换只改变原图形的 ,
不改变原图形的 和 。
位置
形状 大小
1.手扶电梯上的人、笔直轨道上的列车…都在沿着某一方向移动,如果将生活问题数学化,它们都是图形变化中的 。
2.定义:在平面内,将一个图形沿着 移动
,这样的图形运动叫做图形的平移。
一、阅读教材第18--21页的内容,并完成下列问题:
平移
某个方向
一定的距离
3.平移的要素: 与 。
平移的方向 平移的距离
4.把三角形ABC 向右平行移动6格,画出所得到的三角形A′B′C′.
(1)度量三角形ABC与三角形A′B′C′的边、角的大小,你发现了什么?
A
B
C
度量得:
边: ,
,
,
角: ,
,
.
一、阅读教材第18--21页的内容,并完成下列问题:
AB=A′B′ BC=B′C′ AC=A′C′
∠A=∠A′
∠B=∠B′ ∠C=∠C′
4.把三角形ABC 向右平行移动6格,画出所得到的三角形A′B′C′.
(2)连接AA′、BB′、CC′.观察这三条线段的位置有什么关系,测量它们的长度有什么关系?
A
B
C
一、阅读教材第18--21页的内容,并完成下列问题:
A’
B’
C’
结论:
位置关系:
;
数量关系:
;
AA′=BB′=CC′
AA′∥BB′∥CC′
5:(1)如图,怎样平移线段AB可以得到线段PQ?
(2)你能发现线段AP与线段BQ之间的关系吗?
P
B
A
Q
一、阅读教材第18--21页的内容,并完成下列问题:
8
向右平移 个单位长度.
结论:
位置关系:
;
数量关系:
;
AP=BQ
AP∥BQ
一、阅读教材第18--21页的内容,并完成下列问题:
6.(1)下图中的四边形A′B′C′D′是怎样由四边形ABCD平移得到的;
先向右平移 个单位长度,在向下平移 个单位长度。
或者 先向下平移 个单位长度,在向右平移 个单位长度。
9
1
1
9
一、阅读教材第18--21页的内容,并完成下列问题:
6.(2)画出连接对应点的线段AA′、BB′、CC′、DD′.你能发现AA′、BB′、CC′、DD′之间的关系吗?
;
结论:
位置关系:
;
数量关系:
;
AA′=BB′=CC′=DD′
AA′∥BB′∥CC′∥DD′
一、阅读教材第18--21页的内容,并完成下列问题:
6.(3)取线段AD的中点M,画出点M平移后对应的点M′.连接MM′.线段MM′与线段AA′有什么关系?
;
结论:
位置关系:
;
数量关系:
;
AA′=MM′
AA′∥MM′
M
M ′
A
B
P
Q
一、阅读教材第18--21页的内容,并完成下列问题:
一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等.
7.平移的性质:
。
例1.平移三角形ABC,使顶点A移到点D的位置. 画出平移后得到的三角形.
注意:对应点的连线用虚线,用圆规截取相等的相等的线段。保留作图痕迹。
D
C
B
A
二、典型例题:
1.在下面的六幅图案中,(2)、(3)、(4)、(5)、(6)中的哪个图案可以通过平移图案(1)得到?( )
3
三、例题巩固:
2.将A图案剪成若干小块,再分别平移后能够得到B、C、D中的 ( )
A.0个 B.1个 C.2个 D.3个
三、例题巩固:
C
3.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则下列结论正确的是( )
A. FG=5,∠G=70°
B. EH=5,∠F=70°
C. EF=5,∠F=70°
D. EF=5,∠E=70°
H
G
F
E
D
C
B
A
B
三、例题巩固:
8
m
3
m
4.楼梯的高度3米,水平宽度8米,现要在楼梯的表面铺地毯,地毯每米16元,求购买地毯至少需花多少钱?
B A
E
C D
F
三、例题巩固:
5.将∠ABC向上平移10cm得到∠EFG,如果∠ABC=52°,则∠EFG= °,BF= cm。
10cm
52
B
C
A
F
E
G
O
三、例题巩固:
52° 10
四、拓展延伸:
1.如图,半径为2cm的半圆向右平移5cm所扫过的阴影部分面积为 cm2。
20
2.如图,将△ABC 沿着从A到D的方向平移后得到△DEF,若AB=4cm,BE=3cm,CE=1cm.
(1)指出平移的距离是多少?
(2)求线段BF的长.
F
E
D
C
B
A
四、拓展延伸:
3.如图,将△ABC沿边BC方向向右平移2cm,得到△DEF,则四边形ABFD的周长为20cm,则△ABC的周长为 。
16
四、拓展延伸:
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
