全等三角形的判定

(共13张PPT)
学习目标
1.掌握全等三角形的判定定理“AAS”
2.灵活运用“AAS”来判定三角形的全等
3.培养学生分析问题，解决问题的能力
4.培养学生多思考、多动手的学习习惯
重点难点
重点：对定理“AAS”的理解
难点：灵活运用判定
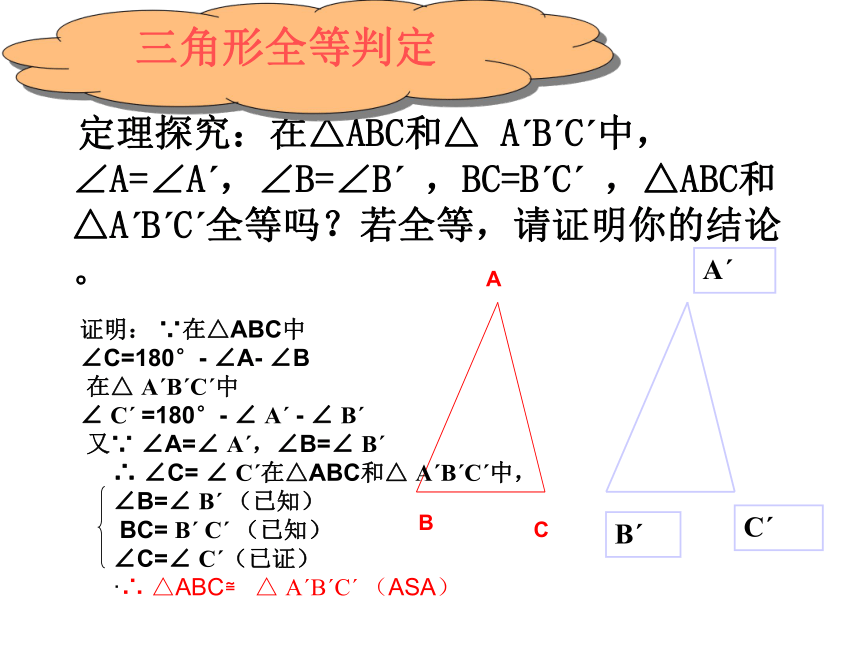
定理探究：在△ABC和△ AˊBˊCˊ中，∠A=∠Aˊ，∠B=∠Bˊ ，BC=BˊCˊ ，△ABC和△AˊBˊCˊ全等吗？若全等，请证明你的结论。
B
C
A
Aˊ
Bˊ
Cˊ
证明： ∵在△ABC中
∠C=180°- ∠A- ∠B
在△ AˊBˊCˊ中
∠ Cˊ =180°- ∠ Aˊ - ∠ Bˊ
又∵ ∠A=∠ Aˊ，∠B=∠ Bˊ
∴ ∠C= ∠ Cˊ在△ABC和△ AˊBˊCˊ中，
∠B=∠ Bˊ （已知）
BC= Bˊ Cˊ （已知）
∠C=∠ Cˊ（已证）
·∴ △ABC≌ △ AˊBˊCˊ （ASA）
三角形全等判定
角边角公理：两角和它们的夹边对应相等的两个三角形全等，可以简写成“角边角”或“ASA”
角角边定理：两个角和其中一个角的对边对应相等的两个三角形全等，可以简写成“角角边”或“AAS”
几何语言叙述：
∠B=∠ Bˊ ∠A= ∠A ˊ
BC= Bˊ Cˊ 或 ∠B=∠ Bˊ
∠C=∠ Cˊ BC= Bˊ Cˊ
△ABC≌ △ AˊBˊCˊ（ASA)△ABC≌ △ AˊBˊCˊ（AAS）
三角形全等判定定理
动手做一做
C
A
B
D
B’
A’
探究试一试
已知，如图，∠ C=∠ D=90°,如果△B DA 沿BA所在直线
平移，如何改变条件，仍用“AAS”,证明：AˊD=AC
∠ B= ∠ A ˊ Bˊ D
探究试一试
已知，如图，将△ Bˊ DAˊ沿BA所在直线翻折后,得到一个新图形BˊEAˊ,这时如何改变条件仍用“AAS”来证明。
C
A
B
D
B’
A’
E
∠ EB ˊ A ˊ= ∠ CBA
探索发现

图形不变,已知和未知变换,又将变成一个新题,你试一试能变几种
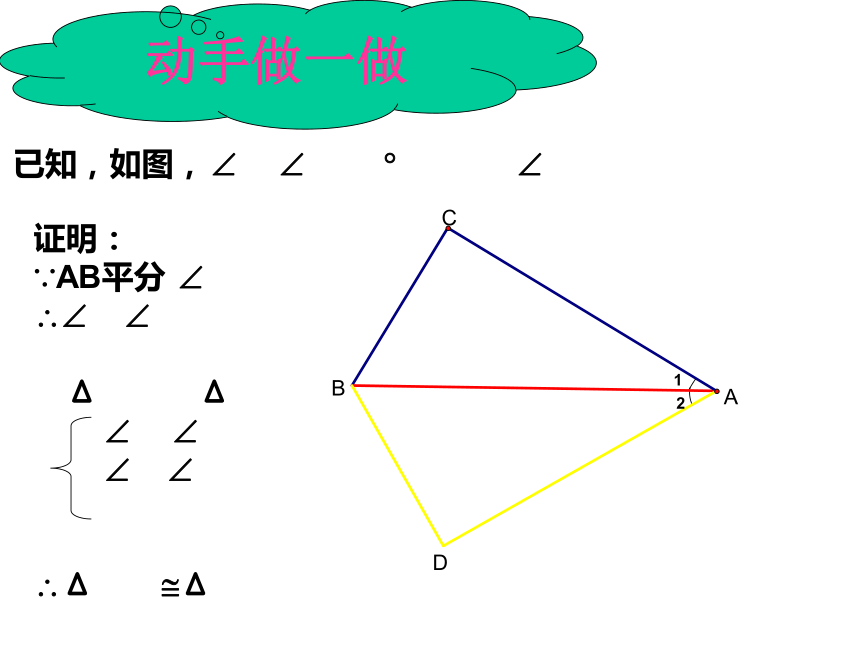
已知:如图,AC=AD,AB平分∠CAD
求证： ∠C= ∠D,BC=BD
探索发现

图形不变,已知和未知变换,又将变成一个新题,你试一试能变几种
已知:如图, AˊD=AC, △B DA 沿BA 所在直线平移, ∠CAB= ∠ Aˊ
求证： ∠C= ∠D,BC=BD
C
A
B
D
B’
A’
探索发现

图形不变,已知和未知变换,又将变成一个新题,你试一试能变几种
已知，如图， △ BˊDAˊ是由△ BCA沿AB翻转再沿AB所在直线平移，现将△ BˊDAˊ沿BA所在直线翻折后,得到一个新图形BˊEAˊ,EAˊ=AC
求证： ∠ C=∠ E
C
A
B
D
B’
A’
E
1.你能总结出我们学过哪些判定三角形
全等的方法吗？
2.要根据题意选择适当的方法。
3.证明线段或角相等，证明它们所在的两个三角形全等。
布置作业