2021年高考数学(理)一轮复习讲义 第1章 1.1 集 合 (Word)
文档属性
| 名称 | 2021年高考数学(理)一轮复习讲义 第1章 1.1 集 合 (Word) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 19:16:47 | ||
图片预览

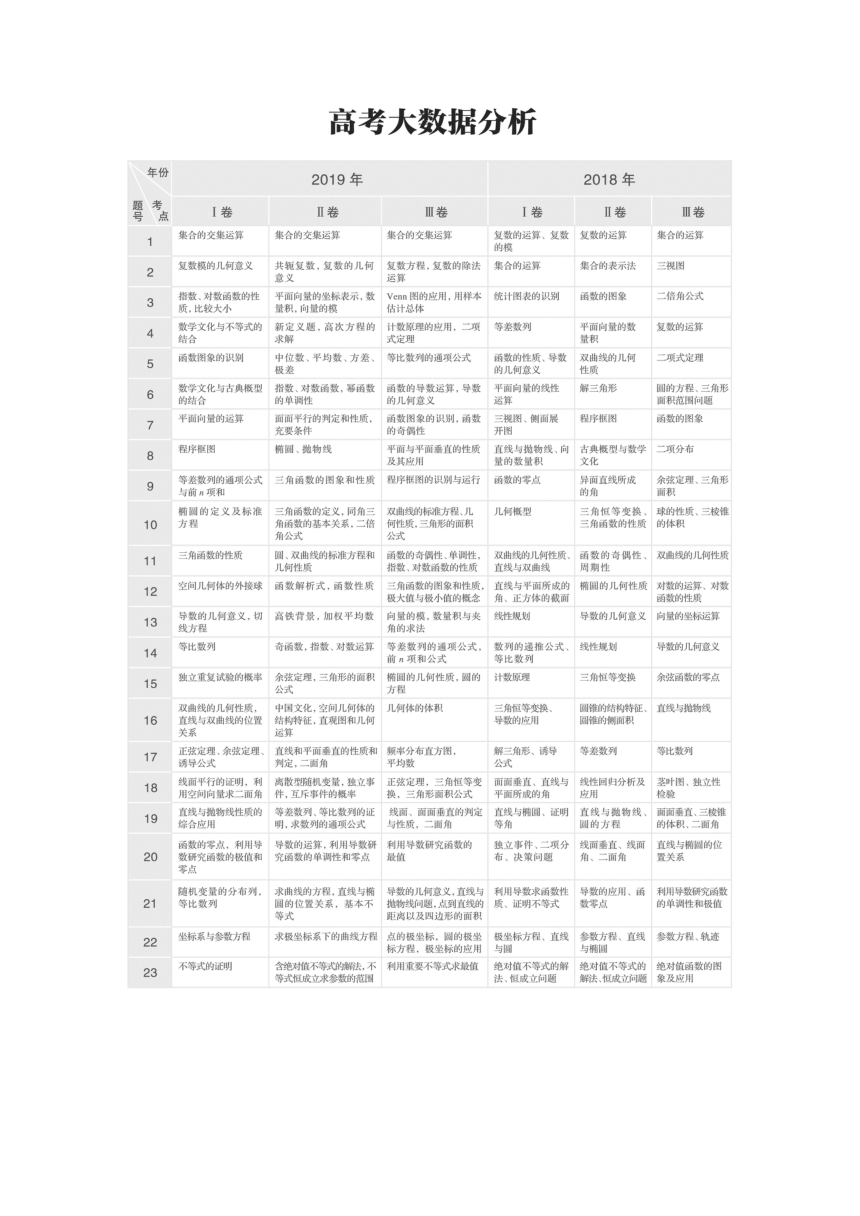



文档简介
§1.1 集 合
最新考纲
考情考向分析
1.了解集合的含义,体会元素与集合的属于关系.
2.能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
3.理解集合之间包含与相等的含义,能识别给定集合的子集.
4.在具体情境中,了解全集与空集的含义.
5.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.
6.理解在给定集合中一个子集的补集的含义,会求给定子集的补集.
7.能使用韦恩(Venn)图表达集合间的基本关系及集合的基本运算.
集合的交、并、补运算及两集合间的包含关系是考查的重点,在集合的运算中经常与不等式、函数相结合,解题时常用到数轴和韦恩(Venn)图.题型以选择题为主,低档难度.
1.集合与元素
(1)集合中元素的三个特征:确定性、互异性、无序性.
(2)元素与集合的关系是属于或不属于,用符号∈或?表示.
(3)集合的表示法:列举法、描述法、图示法.
(4)常见数集的记法
集合
自然数集
正整数集
整数集
有理数集
实数集
符号
N
N
(或N+)
Z
Q
R
2.集合的基本关系
(1)子集:若对于任意的x∈A都有x∈B,则A?B;
(2)真子集:若A?B,且A≠B,则A?B;
(3)相等:若A?B,且B?A,则A=B;
(4)?是任何集合的子集,是任何非空集合的真子集.
3.集合的基本运算
表示
运算
文字语言
集合语言
图形语言
记法
交集
属于A且属于B的所有元素组成的集合
{x|x∈A,且x∈B}
A∩B
并集
属于A或属于B的元素组成的集合
{x|x∈A,或x∈B}
A∪B
补集
全集U中不属于A的元素组成的集合称为集合A相对于集合U的补集
{x|x∈U,x?A}
?UA
概念方法微思考
1.若一个集合A有n个元素,则集合A有几个子集,几个真子集.
提示 2n,2n-1.
2.从A∩B=A,A∪B=A中可以分别得到集合A,B有什么关系?
提示 A∩B=A?A?B,A∪B=A?B?A.
题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)任何一个集合都至少有两个子集.( × )
(2){x|y=x2+1}={y|y=x2+1}={(x,y)|y=x2+1}.( × )
(3)若{x2,1}={0,1},则x=0,1.( × )
(4)若P∩M=P∩N=A,则A?(M∩N).( √ )
题组二 教材改编
2.若集合A={x∈N|x≤},a=2,则下列结论正确的是( )
A.{a}?A
B.a?A
C.{a}∈A
D.a?A
答案 D
3.已知集合A={a,b},若A∪B={a,b,c},满足条件的集合B有________个.
答案 4
解析 因为(A∪B)?B,A={a,b},所以满足条件的集合B可以是{c},{a,c},{b,c},{a,b,c},所以满足条件的集合B有4个.
4.设全集U=R,集合A={x|0≤x≤2},B={y|1≤y≤3},则(?UA)∪B=________.
答案 (-∞,0)∪[1,+∞)
解析 因为?UA={x|x>2或x<0},B={y|1≤y≤3},所以(?UA)∪B=(-∞,0)∪[1,+∞).
题组三 易错自纠
5.已知集合A={1,3,},B={1,m},若B?A,则m=________.
答案 0或3
解析 因为B?A,所以m=3或m=.即m=3或m=0或m=1,根据集合元素的互异性可知m≠1,所以m=0或3.
6.已知集合M={x|x-a=0},N={x|ax-1=0},若M∩N=N,则实数a的值是________.
答案 0或1或-1
解析 易得M={a}.∵M∩N=N,∴N?M,
∴N=?或N=M,∴a=0或a=±1.
集合的含义与表示
1.已知集合A={0,1,2},则集合B={(x,y)|x≥y,x∈A,y∈A}中元素的个数是( )
A.1
B.3
C.6
D.9
答案 C
解析 当x=0时,y=0;当x=1时,y=0或y=1;
当x=2时,y=0,1,2.
故集合B={(0,0),(1,0),(1,1),(2,0),(2,1),(2,2)},即集合B中有6个元素.
2.已知集合A=,则集合A中的元素个数为( )
A.2
B.3
C.4
D.5
答案 C
解析 因为∈Z,且x∈Z,所以2-x的取值有-3,-1,1,3,所以x的值分别为5,3,1,-1,故集合A中的元素个数为4.
3.给出下列四个命题:
①{(x,y)|x=1或y=2}={1,2};
②{x|x=3k+1,k∈-2,k∈Z};
③由英文单词“apple”中的所有字母组成的集合有15个真子集;
④设2
021∈{x,,x2},则满足条件的所有x组成的集合的真子集的个数为3.
其中正确的命题是________.(填序号)
答案 ②③④
解析 ①中左边集合表示横坐标为1,或纵坐标为2的所有点组成的集合,即x=1和y=2两直线上所有点的集合,右边集合表示有两个元素1和2,左、右两集合的元素属性不同.②中3k+1,3k-2(k∈Z)都表示被3除余1的数,易错点在于认为3k+1与3k-2中的k为同一个值,对集合的属性理解错误.③中集合有4个元素,其真子集的个数为24-1=15(个)
.④中x=-2
021或x=-,满足条件的所有x组成的集合为{-2
021,-},其真子集有22-1=3个.所以②③④正确.
思维升华 解决集合含义问题的关键有三点:一是确定构成集合的元素;二是确定元素的限制条件;三是根据元素的特征(满足的条件)构造关系式解决相应问题.
特别提醒:含字母的集合问题,在求出字母的值后,需要验证集合的元素是否满足互异性.
集合间的基本关系
例1 (1)集合M=,N=,则两集合M,N的关系为( )
A.M∩N=?
B.M=N
C.M?N
D.N?M
答案 D
解析 由题意,对于集合M,当n为偶数时,设n=2k(k∈Z),则x=k+1(k∈Z),当n为奇数时,设n=2k+1(k∈Z),则x=k+1+(k∈Z),∴N?M,故选D.
(2)已知集合A={x∈R|x2-3x+2=0},B={x∈N|0答案 4
解析 由题意可得,A={1,2},B={1,2,3,4}.
又∵A?C?B,∴C={1,2}或{1,2,3}或{1,2,4}或{1,2,3,4},∴有4个.
(3)已知集合A={x|x2-2
021x+2
020<0},B={x|x答案 [2
020,+∞)
解析 由x2-2
021x+2
020<0,解得1020,
故A={x|1020}.
又B={x|x020.
思维升华 (1)空集是任何集合的子集,在涉及集合关系时,必须考虑空集的情况,否则易造成漏解.
(2)已知两个集合间的关系求参数时,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的关系,常用数轴、Venn图等来直观解决这类问题.
跟踪训练1 (1)已知集合A={x|y=},B={x|x=m2,m∈A},则( )
A.A?B
B.B?A
C.A?B
D.B=A
答案 B
解析 由题意知A={x|y=},
所以A={x|-1≤x≤1}.
所以B={x|x=m2,m∈A}={x|0≤x≤1},
所以B?A,故选B.
(2)已知集合A={x|(x+1)(x-6)≤0},B={x|m-1≤x≤2m+1}.若B?A,则实数m的取值范围为________.
答案 (-∞,-2)∪
解析 A={x|-1≤x≤6}.
∵B?A,∴B=?或B≠?.
当B=?时,m-1>2m+1,即m<-2.符合题意.
当B≠?时,
解得0≤m≤.
得m<-2或0≤m≤.
集合的基本运算
命题点1 集合的运算
例2 (1)(2019·日照模拟)已知集合A={x|x2-2x-3≤0},B={x|x<2},则A∩B等于( )
A.(1,3)
B.(1,3]
C.[-1,2)
D.(-1,2)
答案 C
解析 因为A={x|x2-2x-3≤0}={x|-1≤x≤3},B={x|x<2},所以A∩B=[-1,2).
(2)(2019·沈阳检测)已知全集U={1,3,5,7},集合A={1,3},B={3,5},则如图所示的阴影区域表示的集合为( )
A.{3}
B.{7}
C.{3,7}
D.{1,3,5}
答案 B
解析 由图可知,阴影区域为?U(A∪B).由题意知,A∪B={1,3,5},U={1,3,5,7},则由补集的概念知,
?U(A∪B)={7}.故选B.
命题点2 利用集合的运算求参数
例3 (1)(2019·银川模拟)已知集合A={x|x2-3x<0},B={1,a},且A∩B有4个子集,则实数a的取值范围是( )
A.(0,3)
B.(0,1)∪(1,3)
C.(0,1)
D.(-∞,1)∪(3,+∞)
答案 B
解析 因为A∩B有4个子集,所以A∩B中有2个不同的元素,所以a∈A,所以a2-3a<0,解得0(2)已知集合A={x|xA.a<1
B.a≤1
C.a>2
D.a≥2
答案 D
解析 集合B={x|x2-3x+2<0}={x|1由A∩B=B可得B?A,作出数轴如图.
可知a≥2.
本例(2)中,若集合A={x|x>a},其他条件不变,则实数a的取值范围是________.
答案 (-∞,1]
解析 ∵A={x|x>a},B={x|1由B?A结合数轴观察(如图).
可得a≤1.
思维升华 (1)一般来讲,集合中的元素若是离散的,可用Venn图表示;数集中的元素若是连续的,则可用数轴表示,此时要注意端点的情况.
(2)运算过程中要注意集合间的特殊关系的使用,灵活使用这些关系,会使运算简化.
跟踪训练2 (1)(2019·烟台模拟)设全集为R,集合M={x|x>1},N={x∈Z|0≤x≤4},
则(?RM)∩N等于( )
A.{0}
B.{0,1}
C.{0,1,2}
D.{2,3,4}
答案 B
解析 N={0,1,2,3,4},?RM={x|x≤1},
∴(?RM)∩N={0,1}.
(2)设集合A={x|-1≤x<2},B={x|xA.-1B.a>2
C.a≥-1
D.a>-1
答案 D
解析 在数轴上画出集合A,B(如图),
观察可知a>-1.
以集合为背景的信息迁移是近几年高考的热点题型,解决这类问题首先要理解题意,准确把握问题本质,回归到数学问题,其次要用好集合的性质,解决信息迁移后的集合问题.
例1 对于集合M,定义函数fM(x)=对于两个集合A,B,定义集合A△B={x|fA(x)·fB(x)=-1}.已知A={2,4,6,8,10},B={1,2,4,8,12},则用列举法写出集合A△B的结果为________.
答案 {1,6,10,12}
解析 要使fA(x)·fB(x)=-1,必有x∈{x|x∈A且x?B}∪{x|x∈B且x?A}={1,6,10,12},所以A△B={1,6,10,12}.
例2 (2019·湖北武汉部分重点中学联考)对于a,b∈N,规定a
b=集合M={(a,b)|a
b=36,a,b∈N
},则M中元素的个数为( )
A.40
B.41
C.50
D.51
答案 B
解析 由题意知a
b=36,a,b∈N
.若a和b的奇偶性相同,则a+b=36,满足此条件的有1+35,2+34,3+33,…,18+18,共18组,此时点(a,b)有35个;若a和b的奇偶性不同,则a×b=36,满足此条件的有1×36,3×12,4×9,共3组,此时点(a,b)有6个.所以M中元素的个数为41.故选B.
例3 已知集合A={x∈N|x2-2x-3≤0},B={1,3},定义集合A,B之间的运算“
”:A
B={x|x=x1+x2,x1∈A,x2∈B},则A
B中的所有元素数字之和为( )
A.15
B.16
C.20
D.21
答案 D
解析 由x2-2x-3≤0,得(x+1)(x-3)≤0,得A={0,1,2,3}.因为A
B={x|x=x1+x2,x1∈A,x2∈B},所以A
B中的元素有:0+1=1,0+3=3,1+1=2,1+3=4,2+1=3(舍去),2+3=5,3+1=4(舍去),3+3=6,所以A
B={1,2,3,4,5,6},所以A
B中的所有元素数字之和为21.
1.下列各组集合中表示同一集合的是( )
A.M={(3,2)},N={(2,3)}
B.M={2,3},N={3,2}
C.M={(x,y)|x+y=1},N={y|x+y=1}
D.M={2,3},N={(2,3)}
答案 B
2.已知集合A={y|y=|x|-1,x∈R},B={x|x≥2},则下列结论正确的是( )
A.-3∈A
B.3?B
C.A∩B=B
D.A∪B=B
答案 C
解析 由题意知A={y|y≥-1},因此A∩B={x|x≥2}=B,故选C.
3.(2018·全国Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )
A.9
B.8
C.5
D.4
答案 A
解析 将满足x2+y2≤3的整数x,y全部列举出来,即(-1,-1),(-1,0),(-1,1),
(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共有9个.
故选A.
4.已知集合A={x∈N
|x2-3x-4<0},则集合A的真子集有( )
A.7个
B.8个
C.15个
D.16个
答案 A
解析 ∵集合A={x∈N
|x2-3x-4<0}={x∈N
|-1∴集合A中共有3个元素,∴真子集有23-1=7(个).
5.设集合M={-1,1},N=,则下列结论中正确的是( )
A.N?M
B.M?N
C.N∩M=?
D.M∪N=R
答案 B
解析 由题意得,
集合N==,
所以M?N.故选B.
6.设集合A={x∈Z|x2-2x-3≤0},B={0,1},则?AB等于( )
A.{-3,-2,-1}
B.{-1,2,3}
C.{-1,0,1,2,3}
D.{0,1}
答案 B
解析 由题意可知A={-1,0,1,2,3},则?AB={-1,2,3}.故选B.
7.已知全集U={x∈N|x2-5x-6<0},集合A={x∈N|-2A.{3,5}
B.{2,3,5}
C.{2,3,4,5}
D.{3,4,5}
答案 A
解析 由题意知,U={0,1,2,3,4,5},A={0,1,2},则(?UA)∩B={3,5}.故选A.
8.已知集合A={x∈N|x2-2x≤0},B={x|-1≤x≤2},则A∩B的子集个数为( )
A.3
B.4
C.7
D.8
答案 D
解析 ∵A={x∈N|x2-2x≤0}={0,1,2},B={x|-1≤x≤2}.
∴A∩B={0,1,2},∴A∩B的子集个数为23=8.
9.(2017·全国Ⅱ改编)设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=________.
答案 {1,3}
解析 ∵A∩B={1},∴1∈B.
∴1-4+m=0,即m=3.
∴B={x|x2-4x+3=0}={1,3}.
10.(2019·湖北黄石一中模拟)设集合M={y|y=2cos
x,x∈[0,5]},N={x|y=log2(x-1)},则M∩N=________.
答案 {x|1解析 ∵M={y|y=2cos
x,x∈[0,5]}={y|-2≤y≤2},N={x|y=log2(x-1)}={x|x>1},
∴M∩N={y|-2≤y≤2}∩{x|x>1}={x|111.设集合A={-1,1,2},B={a+1,a2-2},若A∩B={-1,2},则a的值为________.
答案 -2或1
解析 ∵集合A={-1,1,2},B={a+1,a2-2},A∩B={-1,2},
∴或解得a=-2或a=1.
经检验,a=-2和a=1均满足题意.
12.已知集合A={x|y=lg(x-x2)},B={x|x2-cx<0,c>0},若A?B,则实数c的取值范围是________.
答案 [1,+∞)
解析 由题意知,A={x|y=lg(x-x2)}={x|x-x2>0}=(0,1),B={x|x2-cx<0,c>0}=(0,c).由A?B,画出数轴,如图所示,得c≥1.
13.已知集合A={x∈R||x+2|<3},集合B={x∈R|(x-m)(x-2)<0},且A∩B=(-1,n),则m=______,n=________.
答案 -1 1
解析 A={x∈R||x+2|<3}={x∈R|-5由A∩B=(-1,n),可知m<1,
则B={x|m14.设常数a∈R,集合A={x|(x-1)(x-a)≥0},B={x|x≥a-1},若A∪B=R,则a的取值范围为________.
答案 (-∞,2]
解析 当a>1时,A=(-∞,1]∪[a,+∞),B=[a-1,+∞),当且仅当a-1≤1时,A∪B=R,故115.已知A=,B={x|x2-2x+1-a2≤0}(a>0),若A∪B=B,则实数a的取值范围是______.
答案 [5,+∞)
解析 由>0可得(x-2)(x-6)<0,
∴2x2-2x+1-a2≤0可化为[x-(1-a)][x-(1+a)]≤0.
又a>0,∴B=[1-a,1+a].
由A∪B=B,得A?B,
∴∴a≥5.
∴实数a的取值范围是[5,+∞).
16.当两个集合有公共元素,且互不为对方的子集时,我们称这两个集合“相交”.对于集合M={x|ax2-1=0,a>0},N=,若M与N“相交”,则a=________.
答案 1
解析 M=,由=,得a=4,由=1,得a=1.
当a=4时,M=,此时M?N,不合题意;
当a=1时,M={-1,1},满足题意.
最新考纲
考情考向分析
1.了解集合的含义,体会元素与集合的属于关系.
2.能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
3.理解集合之间包含与相等的含义,能识别给定集合的子集.
4.在具体情境中,了解全集与空集的含义.
5.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.
6.理解在给定集合中一个子集的补集的含义,会求给定子集的补集.
7.能使用韦恩(Venn)图表达集合间的基本关系及集合的基本运算.
集合的交、并、补运算及两集合间的包含关系是考查的重点,在集合的运算中经常与不等式、函数相结合,解题时常用到数轴和韦恩(Venn)图.题型以选择题为主,低档难度.
1.集合与元素
(1)集合中元素的三个特征:确定性、互异性、无序性.
(2)元素与集合的关系是属于或不属于,用符号∈或?表示.
(3)集合的表示法:列举法、描述法、图示法.
(4)常见数集的记法
集合
自然数集
正整数集
整数集
有理数集
实数集
符号
N
N
(或N+)
Z
Q
R
2.集合的基本关系
(1)子集:若对于任意的x∈A都有x∈B,则A?B;
(2)真子集:若A?B,且A≠B,则A?B;
(3)相等:若A?B,且B?A,则A=B;
(4)?是任何集合的子集,是任何非空集合的真子集.
3.集合的基本运算
表示
运算
文字语言
集合语言
图形语言
记法
交集
属于A且属于B的所有元素组成的集合
{x|x∈A,且x∈B}
A∩B
并集
属于A或属于B的元素组成的集合
{x|x∈A,或x∈B}
A∪B
补集
全集U中不属于A的元素组成的集合称为集合A相对于集合U的补集
{x|x∈U,x?A}
?UA
概念方法微思考
1.若一个集合A有n个元素,则集合A有几个子集,几个真子集.
提示 2n,2n-1.
2.从A∩B=A,A∪B=A中可以分别得到集合A,B有什么关系?
提示 A∩B=A?A?B,A∪B=A?B?A.
题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)任何一个集合都至少有两个子集.( × )
(2){x|y=x2+1}={y|y=x2+1}={(x,y)|y=x2+1}.( × )
(3)若{x2,1}={0,1},则x=0,1.( × )
(4)若P∩M=P∩N=A,则A?(M∩N).( √ )
题组二 教材改编
2.若集合A={x∈N|x≤},a=2,则下列结论正确的是( )
A.{a}?A
B.a?A
C.{a}∈A
D.a?A
答案 D
3.已知集合A={a,b},若A∪B={a,b,c},满足条件的集合B有________个.
答案 4
解析 因为(A∪B)?B,A={a,b},所以满足条件的集合B可以是{c},{a,c},{b,c},{a,b,c},所以满足条件的集合B有4个.
4.设全集U=R,集合A={x|0≤x≤2},B={y|1≤y≤3},则(?UA)∪B=________.
答案 (-∞,0)∪[1,+∞)
解析 因为?UA={x|x>2或x<0},B={y|1≤y≤3},所以(?UA)∪B=(-∞,0)∪[1,+∞).
题组三 易错自纠
5.已知集合A={1,3,},B={1,m},若B?A,则m=________.
答案 0或3
解析 因为B?A,所以m=3或m=.即m=3或m=0或m=1,根据集合元素的互异性可知m≠1,所以m=0或3.
6.已知集合M={x|x-a=0},N={x|ax-1=0},若M∩N=N,则实数a的值是________.
答案 0或1或-1
解析 易得M={a}.∵M∩N=N,∴N?M,
∴N=?或N=M,∴a=0或a=±1.
集合的含义与表示
1.已知集合A={0,1,2},则集合B={(x,y)|x≥y,x∈A,y∈A}中元素的个数是( )
A.1
B.3
C.6
D.9
答案 C
解析 当x=0时,y=0;当x=1时,y=0或y=1;
当x=2时,y=0,1,2.
故集合B={(0,0),(1,0),(1,1),(2,0),(2,1),(2,2)},即集合B中有6个元素.
2.已知集合A=,则集合A中的元素个数为( )
A.2
B.3
C.4
D.5
答案 C
解析 因为∈Z,且x∈Z,所以2-x的取值有-3,-1,1,3,所以x的值分别为5,3,1,-1,故集合A中的元素个数为4.
3.给出下列四个命题:
①{(x,y)|x=1或y=2}={1,2};
②{x|x=3k+1,k∈-2,k∈Z};
③由英文单词“apple”中的所有字母组成的集合有15个真子集;
④设2
021∈{x,,x2},则满足条件的所有x组成的集合的真子集的个数为3.
其中正确的命题是________.(填序号)
答案 ②③④
解析 ①中左边集合表示横坐标为1,或纵坐标为2的所有点组成的集合,即x=1和y=2两直线上所有点的集合,右边集合表示有两个元素1和2,左、右两集合的元素属性不同.②中3k+1,3k-2(k∈Z)都表示被3除余1的数,易错点在于认为3k+1与3k-2中的k为同一个值,对集合的属性理解错误.③中集合有4个元素,其真子集的个数为24-1=15(个)
.④中x=-2
021或x=-,满足条件的所有x组成的集合为{-2
021,-},其真子集有22-1=3个.所以②③④正确.
思维升华 解决集合含义问题的关键有三点:一是确定构成集合的元素;二是确定元素的限制条件;三是根据元素的特征(满足的条件)构造关系式解决相应问题.
特别提醒:含字母的集合问题,在求出字母的值后,需要验证集合的元素是否满足互异性.
集合间的基本关系
例1 (1)集合M=,N=,则两集合M,N的关系为( )
A.M∩N=?
B.M=N
C.M?N
D.N?M
答案 D
解析 由题意,对于集合M,当n为偶数时,设n=2k(k∈Z),则x=k+1(k∈Z),当n为奇数时,设n=2k+1(k∈Z),则x=k+1+(k∈Z),∴N?M,故选D.
(2)已知集合A={x∈R|x2-3x+2=0},B={x∈N|0
解析 由题意可得,A={1,2},B={1,2,3,4}.
又∵A?C?B,∴C={1,2}或{1,2,3}或{1,2,4}或{1,2,3,4},∴有4个.
(3)已知集合A={x|x2-2
021x+2
020<0},B={x|x
020,+∞)
解析 由x2-2
021x+2
020<0,解得1
故A={x|1
又B={x|x
思维升华 (1)空集是任何集合的子集,在涉及集合关系时,必须考虑空集的情况,否则易造成漏解.
(2)已知两个集合间的关系求参数时,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的关系,常用数轴、Venn图等来直观解决这类问题.
跟踪训练1 (1)已知集合A={x|y=},B={x|x=m2,m∈A},则( )
A.A?B
B.B?A
C.A?B
D.B=A
答案 B
解析 由题意知A={x|y=},
所以A={x|-1≤x≤1}.
所以B={x|x=m2,m∈A}={x|0≤x≤1},
所以B?A,故选B.
(2)已知集合A={x|(x+1)(x-6)≤0},B={x|m-1≤x≤2m+1}.若B?A,则实数m的取值范围为________.
答案 (-∞,-2)∪
解析 A={x|-1≤x≤6}.
∵B?A,∴B=?或B≠?.
当B=?时,m-1>2m+1,即m<-2.符合题意.
当B≠?时,
解得0≤m≤.
得m<-2或0≤m≤.
集合的基本运算
命题点1 集合的运算
例2 (1)(2019·日照模拟)已知集合A={x|x2-2x-3≤0},B={x|x<2},则A∩B等于( )
A.(1,3)
B.(1,3]
C.[-1,2)
D.(-1,2)
答案 C
解析 因为A={x|x2-2x-3≤0}={x|-1≤x≤3},B={x|x<2},所以A∩B=[-1,2).
(2)(2019·沈阳检测)已知全集U={1,3,5,7},集合A={1,3},B={3,5},则如图所示的阴影区域表示的集合为( )
A.{3}
B.{7}
C.{3,7}
D.{1,3,5}
答案 B
解析 由图可知,阴影区域为?U(A∪B).由题意知,A∪B={1,3,5},U={1,3,5,7},则由补集的概念知,
?U(A∪B)={7}.故选B.
命题点2 利用集合的运算求参数
例3 (1)(2019·银川模拟)已知集合A={x|x2-3x<0},B={1,a},且A∩B有4个子集,则实数a的取值范围是( )
A.(0,3)
B.(0,1)∪(1,3)
C.(0,1)
D.(-∞,1)∪(3,+∞)
答案 B
解析 因为A∩B有4个子集,所以A∩B中有2个不同的元素,所以a∈A,所以a2-3a<0,解得0
B.a≤1
C.a>2
D.a≥2
答案 D
解析 集合B={x|x2-3x+2<0}={x|1
可知a≥2.
本例(2)中,若集合A={x|x>a},其他条件不变,则实数a的取值范围是________.
答案 (-∞,1]
解析 ∵A={x|x>a},B={x|1
可得a≤1.
思维升华 (1)一般来讲,集合中的元素若是离散的,可用Venn图表示;数集中的元素若是连续的,则可用数轴表示,此时要注意端点的情况.
(2)运算过程中要注意集合间的特殊关系的使用,灵活使用这些关系,会使运算简化.
跟踪训练2 (1)(2019·烟台模拟)设全集为R,集合M={x|x>1},N={x∈Z|0≤x≤4},
则(?RM)∩N等于( )
A.{0}
B.{0,1}
C.{0,1,2}
D.{2,3,4}
答案 B
解析 N={0,1,2,3,4},?RM={x|x≤1},
∴(?RM)∩N={0,1}.
(2)设集合A={x|-1≤x<2},B={x|x
C.a≥-1
D.a>-1
答案 D
解析 在数轴上画出集合A,B(如图),
观察可知a>-1.
以集合为背景的信息迁移是近几年高考的热点题型,解决这类问题首先要理解题意,准确把握问题本质,回归到数学问题,其次要用好集合的性质,解决信息迁移后的集合问题.
例1 对于集合M,定义函数fM(x)=对于两个集合A,B,定义集合A△B={x|fA(x)·fB(x)=-1}.已知A={2,4,6,8,10},B={1,2,4,8,12},则用列举法写出集合A△B的结果为________.
答案 {1,6,10,12}
解析 要使fA(x)·fB(x)=-1,必有x∈{x|x∈A且x?B}∪{x|x∈B且x?A}={1,6,10,12},所以A△B={1,6,10,12}.
例2 (2019·湖北武汉部分重点中学联考)对于a,b∈N,规定a
b=集合M={(a,b)|a
b=36,a,b∈N
},则M中元素的个数为( )
A.40
B.41
C.50
D.51
答案 B
解析 由题意知a
b=36,a,b∈N
.若a和b的奇偶性相同,则a+b=36,满足此条件的有1+35,2+34,3+33,…,18+18,共18组,此时点(a,b)有35个;若a和b的奇偶性不同,则a×b=36,满足此条件的有1×36,3×12,4×9,共3组,此时点(a,b)有6个.所以M中元素的个数为41.故选B.
例3 已知集合A={x∈N|x2-2x-3≤0},B={1,3},定义集合A,B之间的运算“
”:A
B={x|x=x1+x2,x1∈A,x2∈B},则A
B中的所有元素数字之和为( )
A.15
B.16
C.20
D.21
答案 D
解析 由x2-2x-3≤0,得(x+1)(x-3)≤0,得A={0,1,2,3}.因为A
B={x|x=x1+x2,x1∈A,x2∈B},所以A
B中的元素有:0+1=1,0+3=3,1+1=2,1+3=4,2+1=3(舍去),2+3=5,3+1=4(舍去),3+3=6,所以A
B={1,2,3,4,5,6},所以A
B中的所有元素数字之和为21.
1.下列各组集合中表示同一集合的是( )
A.M={(3,2)},N={(2,3)}
B.M={2,3},N={3,2}
C.M={(x,y)|x+y=1},N={y|x+y=1}
D.M={2,3},N={(2,3)}
答案 B
2.已知集合A={y|y=|x|-1,x∈R},B={x|x≥2},则下列结论正确的是( )
A.-3∈A
B.3?B
C.A∩B=B
D.A∪B=B
答案 C
解析 由题意知A={y|y≥-1},因此A∩B={x|x≥2}=B,故选C.
3.(2018·全国Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )
A.9
B.8
C.5
D.4
答案 A
解析 将满足x2+y2≤3的整数x,y全部列举出来,即(-1,-1),(-1,0),(-1,1),
(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1),共有9个.
故选A.
4.已知集合A={x∈N
|x2-3x-4<0},则集合A的真子集有( )
A.7个
B.8个
C.15个
D.16个
答案 A
解析 ∵集合A={x∈N
|x2-3x-4<0}={x∈N
|-1
5.设集合M={-1,1},N=,则下列结论中正确的是( )
A.N?M
B.M?N
C.N∩M=?
D.M∪N=R
答案 B
解析 由题意得,
集合N==,
所以M?N.故选B.
6.设集合A={x∈Z|x2-2x-3≤0},B={0,1},则?AB等于( )
A.{-3,-2,-1}
B.{-1,2,3}
C.{-1,0,1,2,3}
D.{0,1}
答案 B
解析 由题意可知A={-1,0,1,2,3},则?AB={-1,2,3}.故选B.
7.已知全集U={x∈N|x2-5x-6<0},集合A={x∈N|-2
B.{2,3,5}
C.{2,3,4,5}
D.{3,4,5}
答案 A
解析 由题意知,U={0,1,2,3,4,5},A={0,1,2},则(?UA)∩B={3,5}.故选A.
8.已知集合A={x∈N|x2-2x≤0},B={x|-1≤x≤2},则A∩B的子集个数为( )
A.3
B.4
C.7
D.8
答案 D
解析 ∵A={x∈N|x2-2x≤0}={0,1,2},B={x|-1≤x≤2}.
∴A∩B={0,1,2},∴A∩B的子集个数为23=8.
9.(2017·全国Ⅱ改编)设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=________.
答案 {1,3}
解析 ∵A∩B={1},∴1∈B.
∴1-4+m=0,即m=3.
∴B={x|x2-4x+3=0}={1,3}.
10.(2019·湖北黄石一中模拟)设集合M={y|y=2cos
x,x∈[0,5]},N={x|y=log2(x-1)},则M∩N=________.
答案 {x|1
x,x∈[0,5]}={y|-2≤y≤2},N={x|y=log2(x-1)}={x|x>1},
∴M∩N={y|-2≤y≤2}∩{x|x>1}={x|1
答案 -2或1
解析 ∵集合A={-1,1,2},B={a+1,a2-2},A∩B={-1,2},
∴或解得a=-2或a=1.
经检验,a=-2和a=1均满足题意.
12.已知集合A={x|y=lg(x-x2)},B={x|x2-cx<0,c>0},若A?B,则实数c的取值范围是________.
答案 [1,+∞)
解析 由题意知,A={x|y=lg(x-x2)}={x|x-x2>0}=(0,1),B={x|x2-cx<0,c>0}=(0,c).由A?B,画出数轴,如图所示,得c≥1.
13.已知集合A={x∈R||x+2|<3},集合B={x∈R|(x-m)(x-2)<0},且A∩B=(-1,n),则m=______,n=________.
答案 -1 1
解析 A={x∈R||x+2|<3}={x∈R|-5
则B={x|m
答案 (-∞,2]
解析 当a>1时,A=(-∞,1]∪[a,+∞),B=[a-1,+∞),当且仅当a-1≤1时,A∪B=R,故1
答案 [5,+∞)
解析 由>0可得(x-2)(x-6)<0,
∴2
又a>0,∴B=[1-a,1+a].
由A∪B=B,得A?B,
∴∴a≥5.
∴实数a的取值范围是[5,+∞).
16.当两个集合有公共元素,且互不为对方的子集时,我们称这两个集合“相交”.对于集合M={x|ax2-1=0,a>0},N=,若M与N“相交”,则a=________.
答案 1
解析 M=,由=,得a=4,由=1,得a=1.
当a=4时,M=,此时M?N,不合题意;
当a=1时,M={-1,1},满足题意.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
