2020-2021学年度上学期安徽省桐城市龙河学校 九年级数学期末强化训练一(word版含答案)
文档属性
| 名称 | 2020-2021学年度上学期安徽省桐城市龙河学校 九年级数学期末强化训练一(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 198.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-14 12:57:41 | ||
图片预览


文档简介
2020-2021学年度上学期桐城市龙河学校沪科版九年级数学期末强化训练
一、选择题(每小题4分,共40分)
1.抛物线y=2x2+1的对称轴是( )
A.直线x=
B.直线y=-
C.y轴
D.直线x=2
2.下列图形不一定相似的是( )
A.所有的等边三角形
B.所有的等腰直角三角形
C.所有的菱形
D.所有的正方形
3.若=,则的值是( )
A.
B.
C.
D.
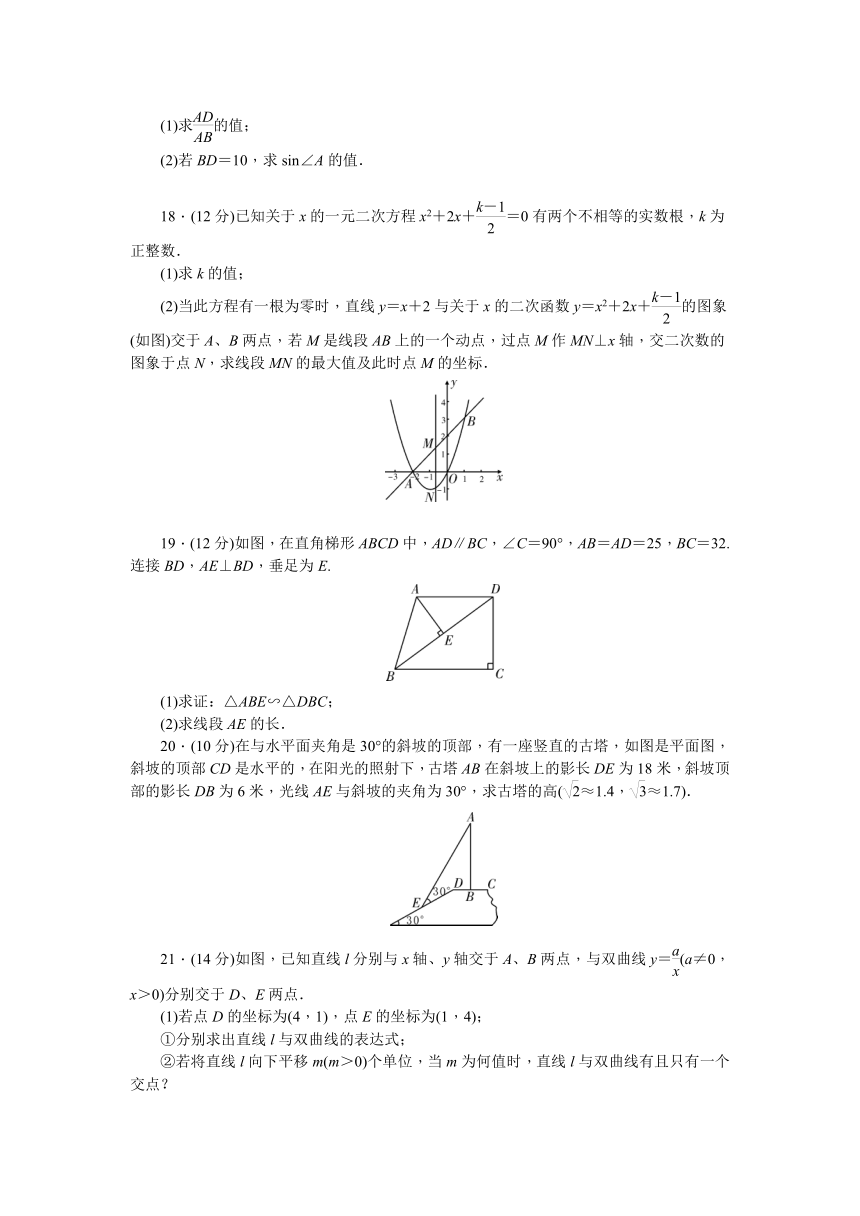
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
A.c>0
B.2a+b=0
C.b2-4ac>0
D.a-b+c>0
第4题图 第5题图 第6题图
5.如图,已知D、E分别是△ABC的AB、AC边上的点,DE∥BC,且S△ADE∶S四边形DBCE=1∶8,那么AE∶AC等于( )
A.1∶9
B.1∶3
C.1∶8
D.1∶2
6.如图,把抛物线y=x2沿直线y=x平移个单位后,其顶点在直线上的A处,则平移后的抛物线表达式是( )
A.y=(x+1)2-1
B.y=(x+1)2+1
C.y=(x-1)2+1
D.y=(x-1)2-1
7.如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为( )
A.-2
B.2
C.4
D.-4
第7题图
第8题图
第9题图
第10题图
8.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
A.20
米
B.10
米
C.15
米
D.5
米
9.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20
m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5
m,两个路灯的高度都是9
m,则两路灯之间的距离是( )
A.24
m
B.25
m
C.28
m
D.30
m
10.如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10
cm,且tan∠EFC=,那么该矩形的周长为( )
A.72
cm
B.36
cm
C.20
cm
D.16
cm
二、填空题(每小题5分,共20分)
11.平移抛物线y=x2+2x-8,使它经过原点,写出平移后抛物线的一个表达式
.
12.对于任意实数t,抛物线y=x2+(2-t)x+t必经过一定点,这个点是
.
13.如图,菱形ABCD的周长为20
cm,且tan∠ABD=,则菱形ABCD的面积为
cm2.
第13题图 第14题图
14.如图,已知矩形OABC的面积为,它的对角线OB与双曲线y=相交于点D,且OB∶OD=5∶3,则k=
.
三、解答题(共90分)
15.(8分)求二次函数y=x2-5x+6与坐标轴的交点坐标及函数的最小值.
16.(8分)如图,已知菱形AMNP内接于△ABC,M、N、P分别在AB、BC、AC上,如果AB=21
cm,AC=15
cm,求菱形AMNP的周长.
17.(12分)如图,在△ABC中,∠C=90°,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9.
(1)求的值;
(2)若BD=10,求sin∠A的值.
18.(12分)已知关于x的一元二次方程x2+2x+=0有两个不相等的实数根,k为正整数.
(1)求k的值;
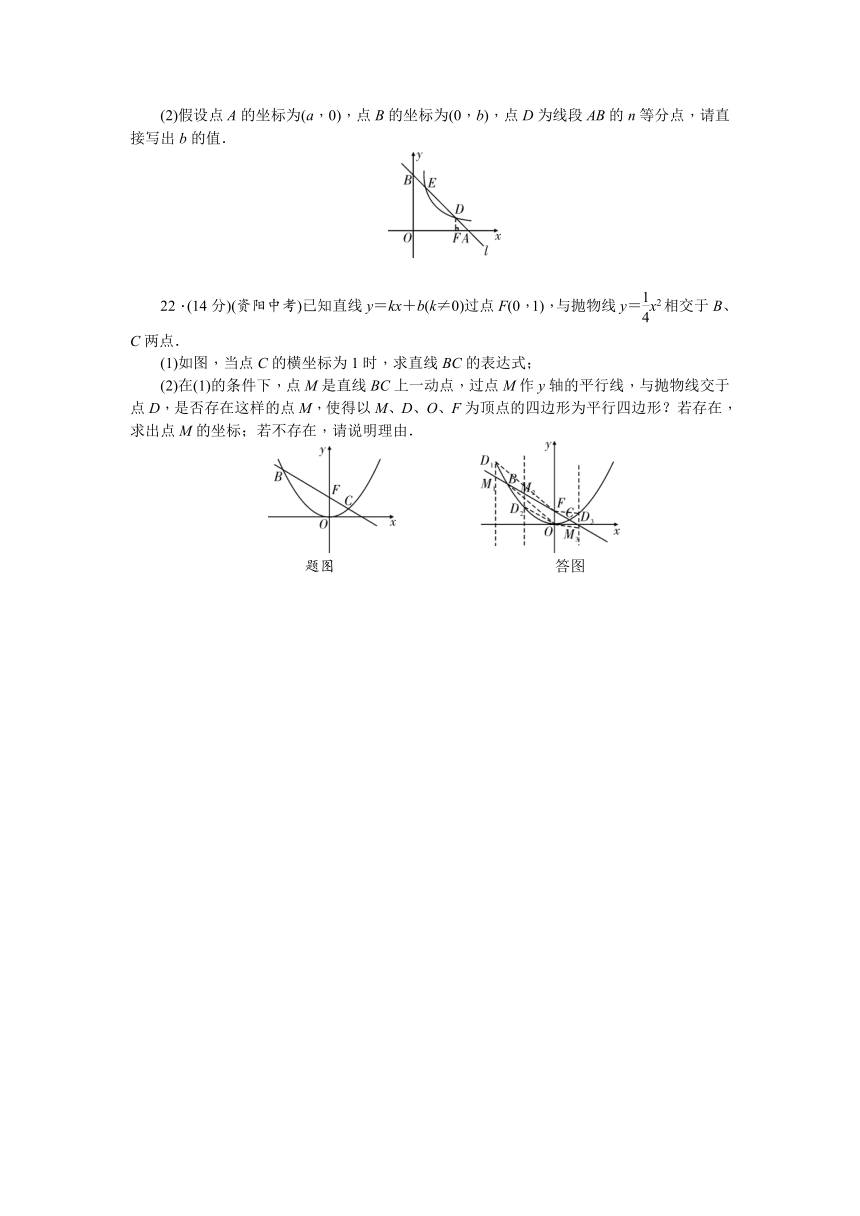
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+的图象(如图)交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次数的图象于点N,求线段MN的最大值及此时点M的坐标.
19.(12分)如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
20.(10分)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高(≈1.4,≈1.7).
21.(14分)如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=(a≠0,x>0)分别交于D、E两点.
(1)若点D的坐标为(4,1),点E的坐标为(1,4);
①分别求出直线l与双曲线的表达式;
②若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.
22.(14分)(资阳中考)已知直线y=kx+b(k≠0)过点F(0,1),与抛物线y=x2相交于B、C两点.
(1)如图,当点C的横坐标为1时,求直线BC的表达式;
(2)在(1)的条件下,点M是直线BC上一动点,过点M作y轴的平行线,与抛物线交于点D,是否存在这样的点M,使得以M、D、O、F为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
题图
答图
参考答案
一、选择题(每小题4分,共40分)
1.抛物线y=2x2+1的对称轴是( C )
A.直线x=
B.直线y=-
C.y轴
D.直线x=2
2.下列图形不一定相似的是( C )
A.所有的等边三角形
B.所有的等腰直角三角形
C.所有的菱形
D.所有的正方形
3.若=,则的值是( A )
A.
B.
C.
D.
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( D )
A.c>0
B.2a+b=0
C.b2-4ac>0
D.a-b+c>0
第4题图 第5题图 第6题图
5.如图,已知D、E分别是△ABC的AB、AC边上的点,DE∥BC,且S△ADE∶S四边形DBCE=1∶8,那么AE∶AC等于( B )
A.1∶9
B.1∶3
C.1∶8
D.1∶2
6.如图,把抛物线y=x2沿直线y=x平移个单位后,其顶点在直线上的A处,则平移后的抛物线表达式是( C )
A.y=(x+1)2-1
B.y=(x+1)2+1
C.y=(x-1)2+1
D.y=(x-1)2-1
7.如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为( A )
A.-2
B.2
C.4
D.-4
第7题图
第8题图
第9题图
第10题图
8.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( A )
A.20
米
B.10
米
C.15
米
D.5
米
9.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20
m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5
m,两个路灯的高度都是9
m,则两路灯之间的距离是( D )
A.24
m
B.25
m
C.28
m
D.30
m
10.如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10
cm,且tan∠EFC=,那么该矩形的周长为( A )
A.72
cm
B.36
cm
C.20
cm
D.16
cm
二、填空题(每小题5分,共20分)
11.平移抛物线y=x2+2x-8,使它经过原点,写出平移后抛物线的一个表达式
如y=x2+2x(答案不唯一,a=1,c=0即可)
.
12.对于任意实数t,抛物线y=x2+(2-t)x+t必经过一定点,这个点是
(1,3)
.
13.如图,菱形ABCD的周长为20
cm,且tan∠ABD=,则菱形ABCD的面积为
24
cm2.
第13题图 第14题图
14.如图,已知矩形OABC的面积为,它的对角线OB与双曲线y=相交于点D,且OB∶OD=5∶3,则k=
12
.
三、解答题(共90分)
15.(8分)求二次函数y=x2-5x+6与坐标轴的交点坐标及函数的最小值.
解:与x轴交点坐标为(2,0),(3,0),与y轴交点坐标为(0,6),最小值为-.
16.(8分)如图,已知菱形AMNP内接于△ABC,M、N、P分别在AB、BC、AC上,如果AB=21
cm,AC=15
cm,求菱形AMNP的周长.
解:∵四边形AMNP是菱形,∴AM=MN,MN∥AC,∴△ABC∽△MBC,∴=,设AM=MN=x
cm,则=,∴x=,∴菱形AMNP的周长=×
4=35(cm).
17.(12分)如图,在△ABC中,∠C=90°,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9.
(1)求的值;
(2)若BD=10,求sin∠A的值.
解:(1);
(2)由(1)知=,∴=,∴AD=BD=5,∴AB=15,∴sin
A==.
18.(12分)已知关于x的一元二次方程x2+2x+=0有两个不相等的实数根,k为正整数.
(1)求k的值;
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+的图象(如图)交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次数的图象于点N,求线段MN的最大值及此时点M的坐标.
解:(1)∵关于x的一元二次方程有两个不相等的实数根,∴Δ=b2-4ac=4-4×
>
0,∴k-1<
2.∴k<
3,∵k为正整数,∴k为1,2.
(2)把x=0代入方程x2+2x+=0得k=1,此时二次函数为y=x2+2x,此时直线y=x+2与二次函数y=x2+2x的交点为A(-2,0),B(1,3)由题意可设M(m,m+2),其中-2<
m<
1,则N(m,m2+2m),MN=m+2-(m2+2m)=-m2-m+2=-(m+)2+.∴当m=-时,MN的长度最大值为.此时点M的坐标为(-,).
19.(12分)如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
(1)证明:证∠ABE=∠ADB=∠DBC,又∠AEB=∠C=90°,∴△ABE∽△DBC;
(2)解:∵AB=AD,AE⊥BD,∴BD=2BE,由△ABE∽△DBC,得=,
=,2BE2=AB·BC,解得BE=20,∴AE==15.
20.(10分)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高(≈1.4,≈1.7).
解:AB=(18+6)≈28.2米.
21.(14分)如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=(a≠0,x>0)分别交于D、E两点.
(1)若点D的坐标为(4,1),点E的坐标为(1,4);
①分别求出直线l与双曲线的表达式;
②若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.
解:(1)①把D(4,1)代入y=得a=4,所以反比例函数表达式为y=(x>
0);设直线l的表达式为y=kx+t,把D(4,1),E(1,4)代入得直线l的表达式为y=-x+5;②直线l向下平移m(m>
0)个单位得到y=-x+5-m,当方程组只有一组解时,直线l与双曲线有且只有一个交点,化为关于x的方程得x2+(m-5)x+4=0,Δ=(m-5)2-4×
4=0,解得m1=1,m2=9,而m=9时,解得x=-2,
故舍去,所以当m=1时,直线l与双曲线有且只有一个交点;
(2)作DF⊥x轴,∵点D为线段AB的n等分点,∴DA∶
AB=1∶
n,∵DF∥OB,∴△ADF∽△ABO,∴==,即==,∴AF=,DF=,∴OF=a-,∴D点坐标为(a-,),把D(a-,)代入y=得(a-)·=a,解得b=.
22.(14分)(资阳中考)已知直线y=kx+b(k≠0)过点F(0,1),与抛物线y=x2相交于B、C两点.
(1)如图,当点C的横坐标为1时,求直线BC的表达式;
(2)在(1)的条件下,点M是直线BC上一动点,过点M作y轴的平行线,与抛物线交于点D,是否存在这样的点M,使得以M、D、O、F为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
题图
答图
解:(1)y=-x+1;
(2)要使以M、D、O、F为顶点的四边形为平行四边形,则MD=OF,如图所示,设M(x,-x+1),则D(x,x2),∵MD∥y轴,∴MD=|-x+1-x2|,由MD=OF,可得|-x+1-x2|=1,①-x+1-x2=1时,解得x1=0(舍)或x1=-3,所以M(-3,),②当-x+1-x2=-1时,解得,x=,所以M(,)或M(,),综上所述,M点坐标为(-3,)或(,)或(,).
一、选择题(每小题4分,共40分)
1.抛物线y=2x2+1的对称轴是( )
A.直线x=
B.直线y=-
C.y轴
D.直线x=2
2.下列图形不一定相似的是( )
A.所有的等边三角形
B.所有的等腰直角三角形
C.所有的菱形
D.所有的正方形
3.若=,则的值是( )
A.
B.
C.
D.
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
A.c>0
B.2a+b=0
C.b2-4ac>0
D.a-b+c>0
第4题图 第5题图 第6题图
5.如图,已知D、E分别是△ABC的AB、AC边上的点,DE∥BC,且S△ADE∶S四边形DBCE=1∶8,那么AE∶AC等于( )
A.1∶9
B.1∶3
C.1∶8
D.1∶2
6.如图,把抛物线y=x2沿直线y=x平移个单位后,其顶点在直线上的A处,则平移后的抛物线表达式是( )
A.y=(x+1)2-1
B.y=(x+1)2+1
C.y=(x-1)2+1
D.y=(x-1)2-1
7.如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为( )
A.-2
B.2
C.4
D.-4
第7题图
第8题图
第9题图
第10题图
8.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
A.20
米
B.10
米
C.15
米
D.5
米
9.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20
m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5
m,两个路灯的高度都是9
m,则两路灯之间的距离是( )
A.24
m
B.25
m
C.28
m
D.30
m
10.如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10
cm,且tan∠EFC=,那么该矩形的周长为( )
A.72
cm
B.36
cm
C.20
cm
D.16
cm
二、填空题(每小题5分,共20分)
11.平移抛物线y=x2+2x-8,使它经过原点,写出平移后抛物线的一个表达式
.
12.对于任意实数t,抛物线y=x2+(2-t)x+t必经过一定点,这个点是
.
13.如图,菱形ABCD的周长为20
cm,且tan∠ABD=,则菱形ABCD的面积为
cm2.
第13题图 第14题图
14.如图,已知矩形OABC的面积为,它的对角线OB与双曲线y=相交于点D,且OB∶OD=5∶3,则k=
.
三、解答题(共90分)
15.(8分)求二次函数y=x2-5x+6与坐标轴的交点坐标及函数的最小值.
16.(8分)如图,已知菱形AMNP内接于△ABC,M、N、P分别在AB、BC、AC上,如果AB=21
cm,AC=15
cm,求菱形AMNP的周长.
17.(12分)如图,在△ABC中,∠C=90°,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9.
(1)求的值;
(2)若BD=10,求sin∠A的值.
18.(12分)已知关于x的一元二次方程x2+2x+=0有两个不相等的实数根,k为正整数.
(1)求k的值;
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+的图象(如图)交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次数的图象于点N,求线段MN的最大值及此时点M的坐标.
19.(12分)如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
20.(10分)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高(≈1.4,≈1.7).
21.(14分)如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=(a≠0,x>0)分别交于D、E两点.
(1)若点D的坐标为(4,1),点E的坐标为(1,4);
①分别求出直线l与双曲线的表达式;
②若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.
22.(14分)(资阳中考)已知直线y=kx+b(k≠0)过点F(0,1),与抛物线y=x2相交于B、C两点.
(1)如图,当点C的横坐标为1时,求直线BC的表达式;
(2)在(1)的条件下,点M是直线BC上一动点,过点M作y轴的平行线,与抛物线交于点D,是否存在这样的点M,使得以M、D、O、F为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
题图
答图
参考答案
一、选择题(每小题4分,共40分)
1.抛物线y=2x2+1的对称轴是( C )
A.直线x=
B.直线y=-
C.y轴
D.直线x=2
2.下列图形不一定相似的是( C )
A.所有的等边三角形
B.所有的等腰直角三角形
C.所有的菱形
D.所有的正方形
3.若=,则的值是( A )
A.
B.
C.
D.
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( D )
A.c>0
B.2a+b=0
C.b2-4ac>0
D.a-b+c>0
第4题图 第5题图 第6题图
5.如图,已知D、E分别是△ABC的AB、AC边上的点,DE∥BC,且S△ADE∶S四边形DBCE=1∶8,那么AE∶AC等于( B )
A.1∶9
B.1∶3
C.1∶8
D.1∶2
6.如图,把抛物线y=x2沿直线y=x平移个单位后,其顶点在直线上的A处,则平移后的抛物线表达式是( C )
A.y=(x+1)2-1
B.y=(x+1)2+1
C.y=(x-1)2+1
D.y=(x-1)2-1
7.如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为( A )
A.-2
B.2
C.4
D.-4
第7题图
第8题图
第9题图
第10题图
8.如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( A )
A.20
米
B.10
米
C.15
米
D.5
米
9.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20
m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5
m,两个路灯的高度都是9
m,则两路灯之间的距离是( D )
A.24
m
B.25
m
C.28
m
D.30
m
10.如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10
cm,且tan∠EFC=,那么该矩形的周长为( A )
A.72
cm
B.36
cm
C.20
cm
D.16
cm
二、填空题(每小题5分,共20分)
11.平移抛物线y=x2+2x-8,使它经过原点,写出平移后抛物线的一个表达式
如y=x2+2x(答案不唯一,a=1,c=0即可)
.
12.对于任意实数t,抛物线y=x2+(2-t)x+t必经过一定点,这个点是
(1,3)
.
13.如图,菱形ABCD的周长为20
cm,且tan∠ABD=,则菱形ABCD的面积为
24
cm2.
第13题图 第14题图
14.如图,已知矩形OABC的面积为,它的对角线OB与双曲线y=相交于点D,且OB∶OD=5∶3,则k=
12
.
三、解答题(共90分)
15.(8分)求二次函数y=x2-5x+6与坐标轴的交点坐标及函数的最小值.
解:与x轴交点坐标为(2,0),(3,0),与y轴交点坐标为(0,6),最小值为-.
16.(8分)如图,已知菱形AMNP内接于△ABC,M、N、P分别在AB、BC、AC上,如果AB=21
cm,AC=15
cm,求菱形AMNP的周长.
解:∵四边形AMNP是菱形,∴AM=MN,MN∥AC,∴△ABC∽△MBC,∴=,设AM=MN=x
cm,则=,∴x=,∴菱形AMNP的周长=×
4=35(cm).
17.(12分)如图,在△ABC中,∠C=90°,点D、E分别在边AB、AC上,DE∥BC,DE=3,BC=9.
(1)求的值;
(2)若BD=10,求sin∠A的值.
解:(1);
(2)由(1)知=,∴=,∴AD=BD=5,∴AB=15,∴sin
A==.
18.(12分)已知关于x的一元二次方程x2+2x+=0有两个不相等的实数根,k为正整数.
(1)求k的值;
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+的图象(如图)交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次数的图象于点N,求线段MN的最大值及此时点M的坐标.
解:(1)∵关于x的一元二次方程有两个不相等的实数根,∴Δ=b2-4ac=4-4×
>
0,∴k-1<
2.∴k<
3,∵k为正整数,∴k为1,2.
(2)把x=0代入方程x2+2x+=0得k=1,此时二次函数为y=x2+2x,此时直线y=x+2与二次函数y=x2+2x的交点为A(-2,0),B(1,3)由题意可设M(m,m+2),其中-2<
m<
1,则N(m,m2+2m),MN=m+2-(m2+2m)=-m2-m+2=-(m+)2+.∴当m=-时,MN的长度最大值为.此时点M的坐标为(-,).
19.(12分)如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
(1)证明:证∠ABE=∠ADB=∠DBC,又∠AEB=∠C=90°,∴△ABE∽△DBC;
(2)解:∵AB=AD,AE⊥BD,∴BD=2BE,由△ABE∽△DBC,得=,
=,2BE2=AB·BC,解得BE=20,∴AE==15.
20.(10分)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高(≈1.4,≈1.7).
解:AB=(18+6)≈28.2米.
21.(14分)如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=(a≠0,x>0)分别交于D、E两点.
(1)若点D的坐标为(4,1),点E的坐标为(1,4);
①分别求出直线l与双曲线的表达式;
②若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.
解:(1)①把D(4,1)代入y=得a=4,所以反比例函数表达式为y=(x>
0);设直线l的表达式为y=kx+t,把D(4,1),E(1,4)代入得直线l的表达式为y=-x+5;②直线l向下平移m(m>
0)个单位得到y=-x+5-m,当方程组只有一组解时,直线l与双曲线有且只有一个交点,化为关于x的方程得x2+(m-5)x+4=0,Δ=(m-5)2-4×
4=0,解得m1=1,m2=9,而m=9时,解得x=-2,
故舍去,所以当m=1时,直线l与双曲线有且只有一个交点;
(2)作DF⊥x轴,∵点D为线段AB的n等分点,∴DA∶
AB=1∶
n,∵DF∥OB,∴△ADF∽△ABO,∴==,即==,∴AF=,DF=,∴OF=a-,∴D点坐标为(a-,),把D(a-,)代入y=得(a-)·=a,解得b=.
22.(14分)(资阳中考)已知直线y=kx+b(k≠0)过点F(0,1),与抛物线y=x2相交于B、C两点.
(1)如图,当点C的横坐标为1时,求直线BC的表达式;
(2)在(1)的条件下,点M是直线BC上一动点,过点M作y轴的平行线,与抛物线交于点D,是否存在这样的点M,使得以M、D、O、F为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
题图
答图
解:(1)y=-x+1;
(2)要使以M、D、O、F为顶点的四边形为平行四边形,则MD=OF,如图所示,设M(x,-x+1),则D(x,x2),∵MD∥y轴,∴MD=|-x+1-x2|,由MD=OF,可得|-x+1-x2|=1,①-x+1-x2=1时,解得x1=0(舍)或x1=-3,所以M(-3,),②当-x+1-x2=-1时,解得,x=,所以M(,)或M(,),综上所述,M点坐标为(-3,)或(,)或(,).
同课章节目录
