北师大版数学九年级上册 第4章相似三角形复习课件(26张)
文档属性
| 名称 | 北师大版数学九年级上册 第4章相似三角形复习课件(26张) |  | |
| 格式 | ppt | ||
| 文件大小 | 352.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 17:59:22 | ||
图片预览




文档简介
第四章 图形的相似复习
北师大版九年级数学上
1、归纳、总结本章知识,使知识成体系。
一、复习目标
2、相似三角形的知识进行巩固提升。
阅读课本P76—117知识要点,弄清一下问题:
1、什么是线段的比?什么是成比例线段?比例有哪些性质?
2、平行线分线段成比例定理及推论是什么?
3、相似多边形的定义,相似三角形的定义,
及相似三角形的判定定理
4、黄金分割的概念,黄金比。
5、相似三角形的性质有哪些?相似多边形呢?
6、什么是位似图形?位似图形有什么性质?在直角坐标系中怎么作关于原点位似的位似图形?
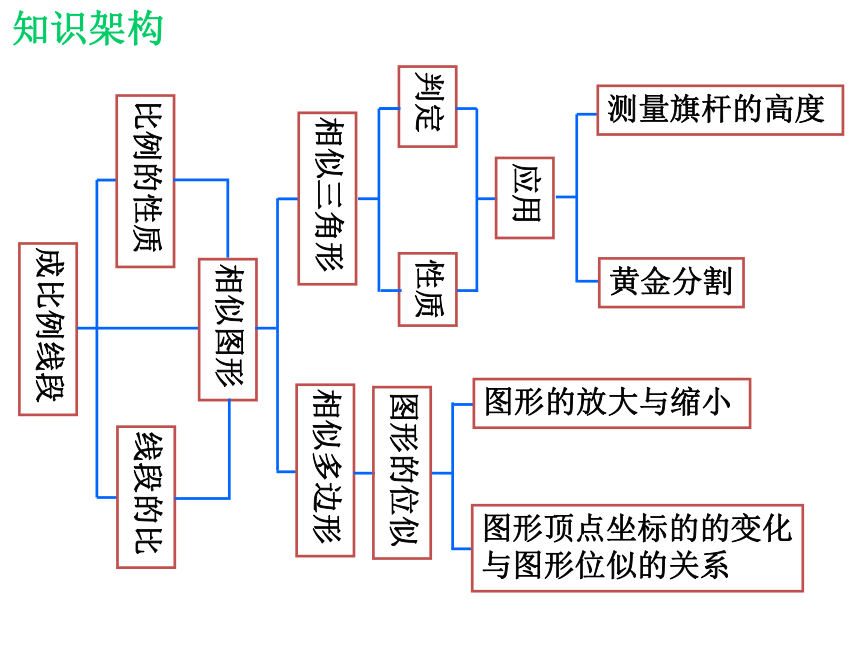
知识架构
成比例线段
比例的性质
线段的比
相似图形
相似三角形
相似多边形
判定
性质
应用
测量旗杆的高度
黄金分割
图形的位似
图形的放大与缩小
图形顶点坐标的的变化
与图形位似的关系
1、四条线段a、b、c、d成比例,其中b=3cm,c=2cm,d=6cm,求线段a的长。
二、巩固提升:
做一做:
2、如果两个相似多边形面积的比为4︰9,那么这两个相似多边形对应边的比是多少?
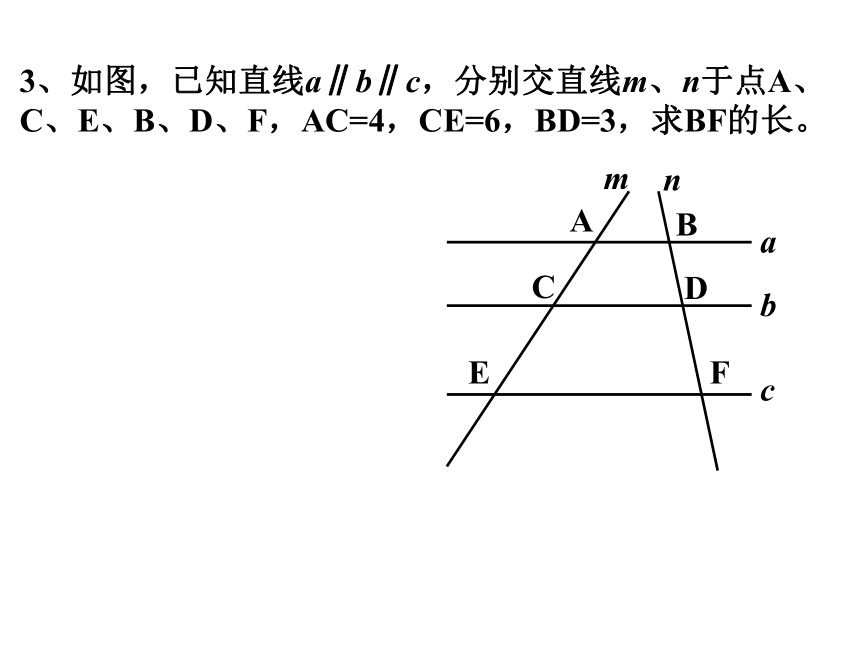
3、如图,已知直线a∥b∥c,分别交直线m、n于点A、C、E、B、D、F,AC=4,CE=6,BD=3,求BF的长。
a
b
c
m
n
A
C
E
B
D
F
A
B
O
C
D
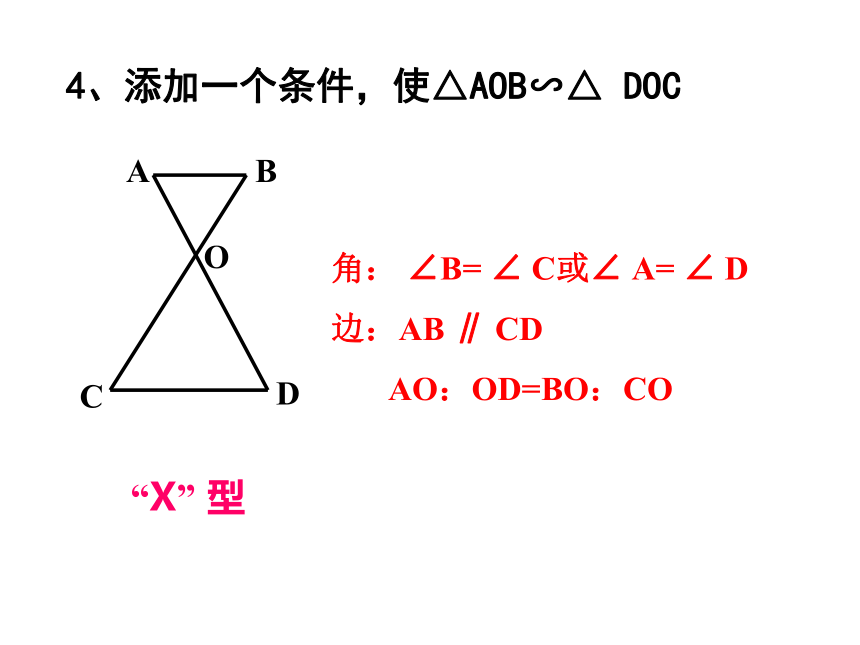
4、添加一个条件,使△AOB∽△ DOC
角: ∠B= ∠ C或∠ A= ∠ D
边:AB ∥ CD
AO:OD=BO:CO
“X” 型
A
B
C
D
E
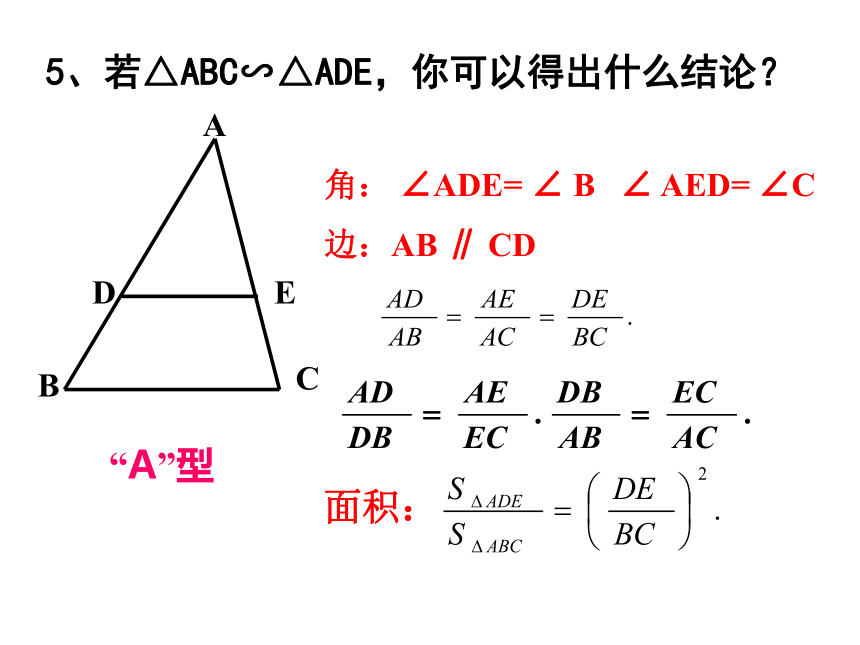
5、若△ABC∽△ADE,你可以得出什么结论?
角: ∠ADE= ∠ B ∠ AED= ∠C
边:AB ∥ CD
面积:
“A”型
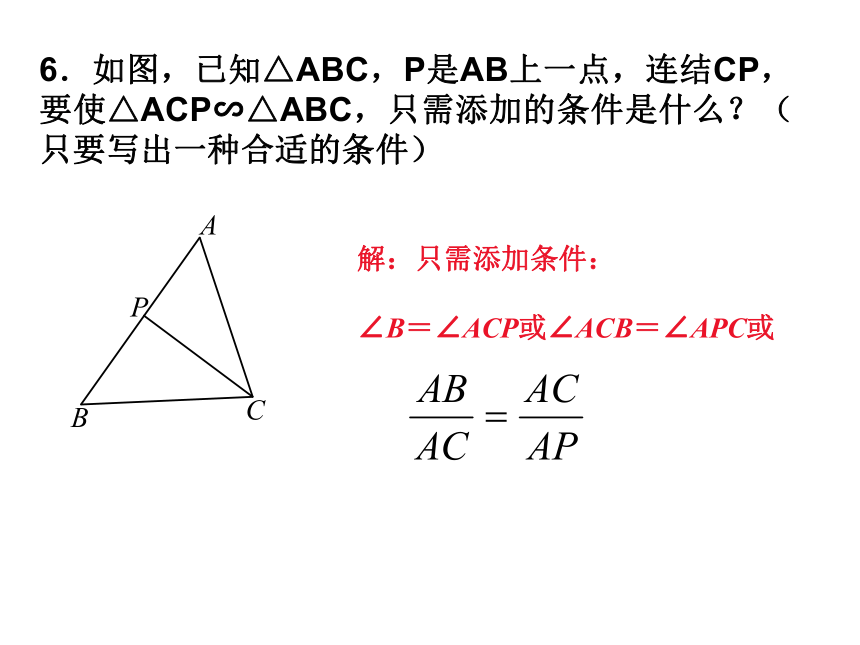
6.如图,已知△ABC,P是AB上一点,连结CP,要使△ACP∽△ABC,只需添加的条件是什么?(只要写出一种合适的条件)
A
B
C
P
解:只需添加条件:
∠B=∠ACP或∠ACB=∠APC或
A
B
C
D
E
1、如图,DE∥BC,D是AB的中点,DC、BE相交于点G。
求
G
知识源于悟
A
B
C
D
E
F
2、如图: DE∥BC,EF ∥AB,AE:EC=2:3,S △ABC=25,求S四边形BDEF
知识源于悟
1、两个相似三角形对应中线之比是1:2,
则对应角平分线之比也是1:2。( )
2、两个相似三角形面积比是1:2,则相似比是1:4。( )
3、△ABC∽△A′B′C′,相似比为2:3,若△ABC周长为6,
则△A′B′C′周长为9。 ( )
二、填空:
1.如图△ABC中,DE∥BC,且S△ADE=S梯形DBCE,
则DE:BC=____.
A
B
C
D
E
一、判断正误:
三、课堂反馈
√
×
√
:2
3.如图,DE∥BC,AD:DB=1:2,DC,BE交于点O,
则△DOE与△BOC的周长之比是_______,
面积比是________.
2.两个相似五边形的面积比为9:16,其中较大
的五边形的周长为64cm,则较小的五边形
的周长为_______cm.
O
D
A
B
C
E
48
1:3
1:9
4、 两相似三角形对应高之比为3∶4,周长之和为28cm,则两个三角形周长分别为
12cm与16cm
5、 两相似三角形的相似比为3∶5,它们的面积和为102cm2,则较大三角形的面积为
75cm2
6. 四边形ABCD是平行四边形,点E是 BC的延长线上的一点,而CE:BC=1:3,则 △ADG和△EBG的周长比 ,面积比为
F
D
G
E
B
A
C
3:4
9:16
四、小结:本节课你有什么收获?
五、作业
完成课本复习题
A
E
B
F
D
C
1、如图,在 ABCD中,E是BC上一点, BE:EC=1:2,AE与BD相交于F,则 BF:FD=_______,S △ADF : S △EBF =______
1:3
1:9
四、课堂反馈:
2、如图,能保证使△ACD与△ABC相似的
条件是( )
C
A
B
D
(1)AC︰CD = AB︰BC
(2)CD︰AD = BC︰AC
(3)AC = AD · AB
2
(4)CD = AD · AB
2
C
3、如图,在△ABC中,已知DE//BC,AD=3BD,
S
△ABC
=48,求
S
△ADE
A
B
C
D
E
1、如图,在△ABC中,∠BAC=90°,AB=6,BC=12,点P从A点出发向B以1m/s的速度移动,点Q从B点出发向C点以2m/s的速度移动,如果P、Q分别从A、B两地同时出发,几秒后△ PBQ与原三角形相似?
A
B
C
Q
P
Q
P
选做:
2、如图,AB和CD表示两根直立于地面的柱子,AD和
BC表示起固定作用的两根钢筋,AD与BC的交点为M,
已知AB=10cm,CD=15cm,求点M离地面的高度MH。
B
A
M
H
D
C
2. 如图,AE2=AD·AB,且∠ABE=∠BCE,
试说明△EBC∽△DEB
B
C
D
E
A
∵ AE2=AD·AB,得AE∶AD=AB∶AE
∵∠A=∠A ∴△AED∽△ABE
∴∠AED=∠ABE∵∠ABE=∠BCE
∴ ∠AED=∠BCE
∴DE∥BC
∴∠DEB=∠EBC ∵∠ABE=∠BCE
∴ △EBC∽△DEB
解:
3、如图,在△ABC中,∠BAC=90°,AB=6,BC=12,点P从A点出发向B以1m/s的速度移动,点Q从B点出发向C点以2m/s的速度移动,如果P、Q分别从A、B两地同时出发,几秒后△ PBQ与原三角形相似?
A
B
C
Q
P
Q
P
4.如图?ABC中,AB=8cm,BC=16cm,点P从A点开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动。若点P、Q从A、B处同时出发,经过几秒钟后,?PBQ与?ABC相似?
Q
P
C
B
A
学以致用:
本节课主要是复习相似三角形的性质
判定及其运用。在解题中要熟悉基本图
形。并能从条件和结论两方面同时考虑问
题。灵活应用。
回顾与反思
不是你比别人差,只是付出不够多。
北师大版九年级数学上
1、归纳、总结本章知识,使知识成体系。
一、复习目标
2、相似三角形的知识进行巩固提升。
阅读课本P76—117知识要点,弄清一下问题:
1、什么是线段的比?什么是成比例线段?比例有哪些性质?
2、平行线分线段成比例定理及推论是什么?
3、相似多边形的定义,相似三角形的定义,
及相似三角形的判定定理
4、黄金分割的概念,黄金比。
5、相似三角形的性质有哪些?相似多边形呢?
6、什么是位似图形?位似图形有什么性质?在直角坐标系中怎么作关于原点位似的位似图形?
知识架构
成比例线段
比例的性质
线段的比
相似图形
相似三角形
相似多边形
判定
性质
应用
测量旗杆的高度
黄金分割
图形的位似
图形的放大与缩小
图形顶点坐标的的变化
与图形位似的关系
1、四条线段a、b、c、d成比例,其中b=3cm,c=2cm,d=6cm,求线段a的长。
二、巩固提升:
做一做:
2、如果两个相似多边形面积的比为4︰9,那么这两个相似多边形对应边的比是多少?
3、如图,已知直线a∥b∥c,分别交直线m、n于点A、C、E、B、D、F,AC=4,CE=6,BD=3,求BF的长。
a
b
c
m
n
A
C
E
B
D
F
A
B
O
C
D
4、添加一个条件,使△AOB∽△ DOC
角: ∠B= ∠ C或∠ A= ∠ D
边:AB ∥ CD
AO:OD=BO:CO
“X” 型
A
B
C
D
E
5、若△ABC∽△ADE,你可以得出什么结论?
角: ∠ADE= ∠ B ∠ AED= ∠C
边:AB ∥ CD
面积:
“A”型
6.如图,已知△ABC,P是AB上一点,连结CP,要使△ACP∽△ABC,只需添加的条件是什么?(只要写出一种合适的条件)
A
B
C
P
解:只需添加条件:
∠B=∠ACP或∠ACB=∠APC或
A
B
C
D
E
1、如图,DE∥BC,D是AB的中点,DC、BE相交于点G。
求
G
知识源于悟
A
B
C
D
E
F
2、如图: DE∥BC,EF ∥AB,AE:EC=2:3,S △ABC=25,求S四边形BDEF
知识源于悟
1、两个相似三角形对应中线之比是1:2,
则对应角平分线之比也是1:2。( )
2、两个相似三角形面积比是1:2,则相似比是1:4。( )
3、△ABC∽△A′B′C′,相似比为2:3,若△ABC周长为6,
则△A′B′C′周长为9。 ( )
二、填空:
1.如图△ABC中,DE∥BC,且S△ADE=S梯形DBCE,
则DE:BC=____.
A
B
C
D
E
一、判断正误:
三、课堂反馈
√
×
√
:2
3.如图,DE∥BC,AD:DB=1:2,DC,BE交于点O,
则△DOE与△BOC的周长之比是_______,
面积比是________.
2.两个相似五边形的面积比为9:16,其中较大
的五边形的周长为64cm,则较小的五边形
的周长为_______cm.
O
D
A
B
C
E
48
1:3
1:9
4、 两相似三角形对应高之比为3∶4,周长之和为28cm,则两个三角形周长分别为
12cm与16cm
5、 两相似三角形的相似比为3∶5,它们的面积和为102cm2,则较大三角形的面积为
75cm2
6. 四边形ABCD是平行四边形,点E是 BC的延长线上的一点,而CE:BC=1:3,则 △ADG和△EBG的周长比 ,面积比为
F
D
G
E
B
A
C
3:4
9:16
四、小结:本节课你有什么收获?
五、作业
完成课本复习题
A
E
B
F
D
C
1、如图,在 ABCD中,E是BC上一点, BE:EC=1:2,AE与BD相交于F,则 BF:FD=_______,S △ADF : S △EBF =______
1:3
1:9
四、课堂反馈:
2、如图,能保证使△ACD与△ABC相似的
条件是( )
C
A
B
D
(1)AC︰CD = AB︰BC
(2)CD︰AD = BC︰AC
(3)AC = AD · AB
2
(4)CD = AD · AB
2
C
3、如图,在△ABC中,已知DE//BC,AD=3BD,
S
△ABC
=48,求
S
△ADE
A
B
C
D
E
1、如图,在△ABC中,∠BAC=90°,AB=6,BC=12,点P从A点出发向B以1m/s的速度移动,点Q从B点出发向C点以2m/s的速度移动,如果P、Q分别从A、B两地同时出发,几秒后△ PBQ与原三角形相似?
A
B
C
Q
P
Q
P
选做:
2、如图,AB和CD表示两根直立于地面的柱子,AD和
BC表示起固定作用的两根钢筋,AD与BC的交点为M,
已知AB=10cm,CD=15cm,求点M离地面的高度MH。
B
A
M
H
D
C
2. 如图,AE2=AD·AB,且∠ABE=∠BCE,
试说明△EBC∽△DEB
B
C
D
E
A
∵ AE2=AD·AB,得AE∶AD=AB∶AE
∵∠A=∠A ∴△AED∽△ABE
∴∠AED=∠ABE∵∠ABE=∠BCE
∴ ∠AED=∠BCE
∴DE∥BC
∴∠DEB=∠EBC ∵∠ABE=∠BCE
∴ △EBC∽△DEB
解:
3、如图,在△ABC中,∠BAC=90°,AB=6,BC=12,点P从A点出发向B以1m/s的速度移动,点Q从B点出发向C点以2m/s的速度移动,如果P、Q分别从A、B两地同时出发,几秒后△ PBQ与原三角形相似?
A
B
C
Q
P
Q
P
4.如图?ABC中,AB=8cm,BC=16cm,点P从A点开始沿AB边向点B以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动。若点P、Q从A、B处同时出发,经过几秒钟后,?PBQ与?ABC相似?
Q
P
C
B
A
学以致用:
本节课主要是复习相似三角形的性质
判定及其运用。在解题中要熟悉基本图
形。并能从条件和结论两方面同时考虑问
题。灵活应用。
回顾与反思
不是你比别人差,只是付出不够多。
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
