华东师大初中数学八年级上册《12.2.2单项式与多项式相乘》课件(共15张PPT)
文档属性
| 名称 | 华东师大初中数学八年级上册《12.2.2单项式与多项式相乘》课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 561.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 18:09:16 | ||
图片预览




文档简介
复习提问:
1.请说出单项式与单项式相乘的法则:
单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
判断正误(如果不对应如何改正?)
(1)
(2)
(3)
单项式与多项式相乘
复习提问:
1. 什么叫多项式?
几个单项式的和叫做多项式。
在多项式中,每个单项式叫做多项式的项。
2. 什么叫多项式的项?
说出多项式 2x2+3x-1的项和各项的系数
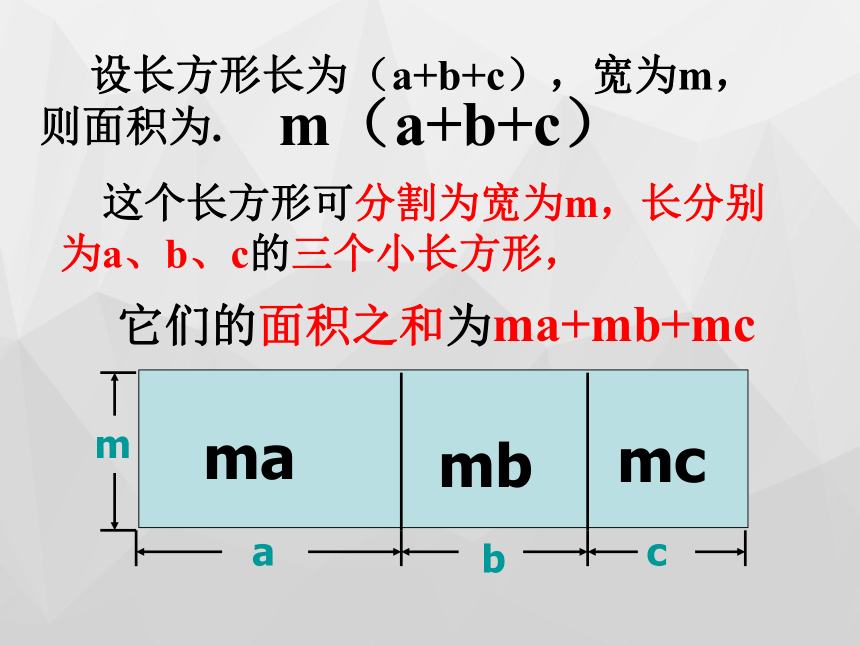
设长方形长为(a+b+c),宽为m,则面积为.
这个长方形可分割为宽为m,长分别为a、b、c的三个小长方形,
m(a+b+c)
m
a
b
c
ma
mb
mc
它们的面积之和为ma+mb+mc
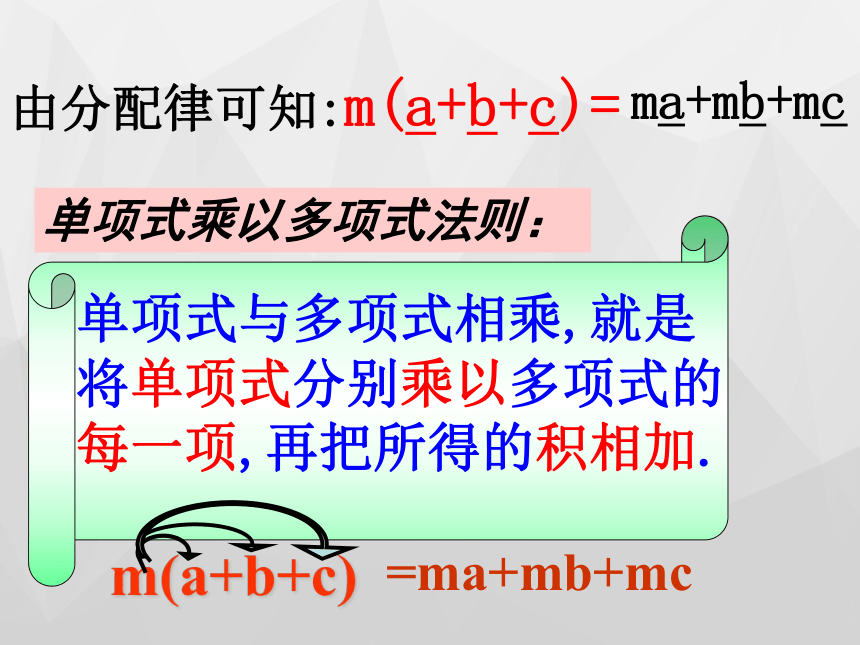
由分配律可知:m(a+b+c)=
ma+mb+mc
单项式乘以多项式法则:
单项式与多项式相乘,就是将单项式分别乘以多项式的每一项,再把所得的积相加.
m(a+b+c)
=ma+mb+mc
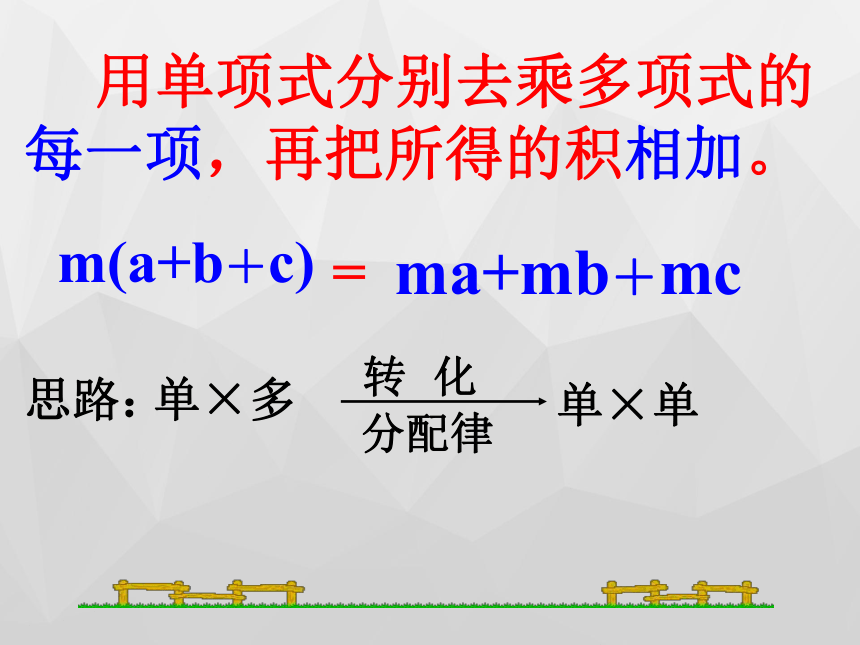
用单项式分别去乘多项式的每一项,再把所得的积相加。
思路:
单×多
转 化
分配律
单×单
m(a+b+c)
=
ma+mb+mc
例1 计算
不要漏乘常数项1
说明:先进行乘方运算,再进行单项式与多项式的乘法运算。注意:多项式的每一项包括它前面的符号
例2 计算:
例3 计算:
注意:
1.将-2a2与-5a的“-”看成性质符号
2.单项式与多项式相乘的结果中,应将同类项合并。
几点注意:
1.单项式乘多项式的结果是多项式,
积的项数与原多项式的项数相同。
3.不要出现漏乘现象,运算要有顺序。
2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:
同号相乘得正,异号相乘得负
.填空
.计算
课时小结:
1、单项式与多项式相乘的实质是利用分配律把单项式乘以多项式转化为单项式乘法
2.单项式与多项式相乘时,分三个阶段:
①按分配律把乘积写成单项式与单项式乘积的代数和的形式;
②按照单项式的乘法法则运算。
③再把所得的积相加.
1. 计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负。
2.不要出现漏乘现象。
3.运算要有顺序:先乘方,再乘除,最后加减。
4.对于混合运算,注意最后应合并同类项。
四点注意:
1.请说出单项式与单项式相乘的法则:
单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
判断正误(如果不对应如何改正?)
(1)
(2)
(3)
单项式与多项式相乘
复习提问:
1. 什么叫多项式?
几个单项式的和叫做多项式。
在多项式中,每个单项式叫做多项式的项。
2. 什么叫多项式的项?
说出多项式 2x2+3x-1的项和各项的系数
设长方形长为(a+b+c),宽为m,则面积为.
这个长方形可分割为宽为m,长分别为a、b、c的三个小长方形,
m(a+b+c)
m
a
b
c
ma
mb
mc
它们的面积之和为ma+mb+mc
由分配律可知:m(a+b+c)=
ma+mb+mc
单项式乘以多项式法则:
单项式与多项式相乘,就是将单项式分别乘以多项式的每一项,再把所得的积相加.
m(a+b+c)
=ma+mb+mc
用单项式分别去乘多项式的每一项,再把所得的积相加。
思路:
单×多
转 化
分配律
单×单
m(a+b+c)
=
ma+mb+mc
例1 计算
不要漏乘常数项1
说明:先进行乘方运算,再进行单项式与多项式的乘法运算。注意:多项式的每一项包括它前面的符号
例2 计算:
例3 计算:
注意:
1.将-2a2与-5a的“-”看成性质符号
2.单项式与多项式相乘的结果中,应将同类项合并。
几点注意:
1.单项式乘多项式的结果是多项式,
积的项数与原多项式的项数相同。
3.不要出现漏乘现象,运算要有顺序。
2.单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:
同号相乘得正,异号相乘得负
.填空
.计算
课时小结:
1、单项式与多项式相乘的实质是利用分配律把单项式乘以多项式转化为单项式乘法
2.单项式与多项式相乘时,分三个阶段:
①按分配律把乘积写成单项式与单项式乘积的代数和的形式;
②按照单项式的乘法法则运算。
③再把所得的积相加.
1. 计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负。
2.不要出现漏乘现象。
3.运算要有顺序:先乘方,再乘除,最后加减。
4.对于混合运算,注意最后应合并同类项。
四点注意:
