华东师大初中数学八年级上册《12.2.3多项式与多项式相乘》课件(共17张PPT)
文档属性
| 名称 | 华东师大初中数学八年级上册《12.2.3多项式与多项式相乘》课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览




文档简介
多项式与多项式相乘
学习目标
课堂小结
巩固练习
例题讲解
复习回顾
学习六步曲
探究新知
1.经历探索多项式与多项式相乘法则的过程,
能够按多项式乘法步骤进行简单的乘法运算,达到熟练地进行多项式的乘法的要求。
?2.通过转化整体和数形结合的数学思想方法,来体验探求数学问题的过程,培养学生的知识迁移、分析问题、解决问题和数学语言表达能力。
?3.发展有条理的思考,逐步形成主动探索的习惯。
回顾与思考
② 再把所得的积相加。
?
如何进行单项式与多项式乘法的运算?
① 将单项式分别乘以多项式的各项,
?
进行单项式与多项式乘法运算时,要注
意什么?
① 不能漏乘:
即单项式要乘遍多项式
的每一项
② 去括号时注意符号的确定.
基本功训练:
(5a2- a+1).(-6a3)
a2(a+1) – a(2a2+a-1)
= - 30a5+4a4-6a3
= -a3+a
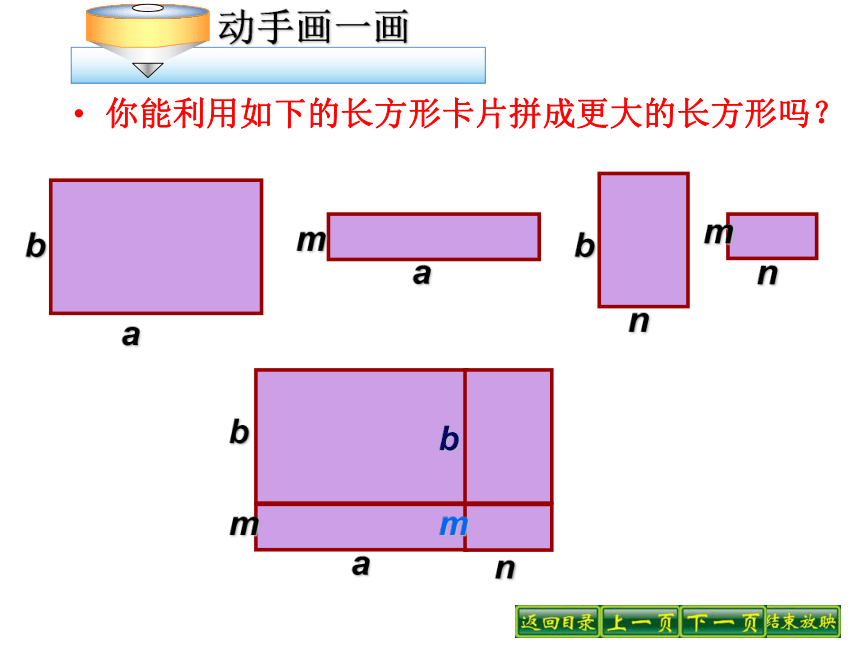
你能利用如下的长方形卡片拼成更大的长方形吗?
a
b
a
m
n
b
n
m
a
b
a
m
n
b
n
m
动手画一画
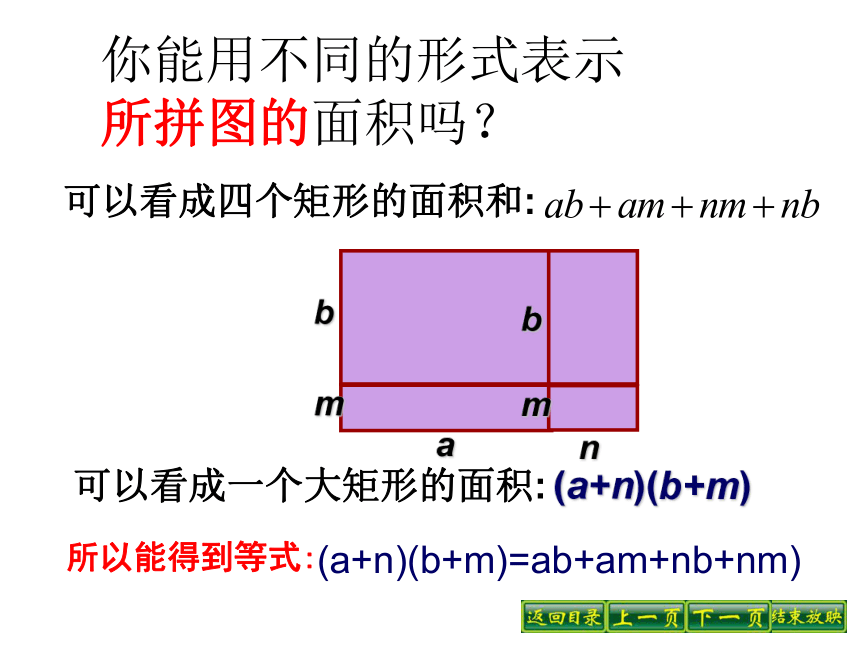
你能用不同的形式表示
所拼图的面积吗?
m
b
a
m
b
b
n
m
可以看成四个矩形的面积和:
可以看成一个大矩形的面积:
(a+n)(b+m)
(a+n)(b+m)=ab+am+nb+nm)
所以能得到等式:
多项式与多项式相乘:
(a+n)(b+m)=
ab
+ am
+ nb
+nm
如何进行多项式与多项式相乘的运算 ?
先用一个多项式的每一项
乘另一个多项式的每一项,
再把所得的积相加。
例1 计算:
①
②
③
④
①
②
③
④
①
②
③
④
注意事项:
1、多项式乘法中,每一项应连同符号相乘;切记“同号得正,异号得负”;
2、要防止漏乘;
例2 计算:
(3x-1)(x+3)
3、多项式相乘的积在没有合并同类项前,所得的项数是两个多项式项数的积;
4、乘积中,有同类项时一定要合并,得到最简结果。
=3x?x
+3x?3
-
1?x
-
1×3
= 3x2 + 8x –3
随堂练习
(1) (m+2n)(m?2n);
(2) (2n +5)(n?3) ;
计算:
(3) (x+2y)2 ;
合作探究
(x+3)(x-5)
(2)(x-3)(x+5)
(3)(x+3)(x+5)
(4)(x-3)(x-5)
请观察上面四题的特点,你能总结出它们结果的规律吗?
=x2-2x-15
=x2+2x-15
=x2+8x+15
=x2-8x+15
例2 计算:
规律:
+
×
练习:用推导的公式计算:
合作探究:
当a为何值时,(x2+ax+1)(x2-3x+2)的运算结果不含有x2项.
先利用多项式与多项式相乘的乘法法则进行计算,然后合并同类项,合并时含有x2的系数和为0即可。
本节课你的收获是什么?
运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.
最后的计算结果要化简 ̄ ̄ ̄
合并同类项.
如何进行多项式与多项式乘法运算?
在寻求真理的长征中,唯有学习,不断地学习,勤奋地学习,有创造地学习,才能越重山,跨峻岭。
——华罗庚
作业:
1.课本第29页练习计算
2.习题12.2第5.6题
学习目标
课堂小结
巩固练习
例题讲解
复习回顾
学习六步曲
探究新知
1.经历探索多项式与多项式相乘法则的过程,
能够按多项式乘法步骤进行简单的乘法运算,达到熟练地进行多项式的乘法的要求。
?2.通过转化整体和数形结合的数学思想方法,来体验探求数学问题的过程,培养学生的知识迁移、分析问题、解决问题和数学语言表达能力。
?3.发展有条理的思考,逐步形成主动探索的习惯。
回顾与思考
② 再把所得的积相加。
?
如何进行单项式与多项式乘法的运算?
① 将单项式分别乘以多项式的各项,
?
进行单项式与多项式乘法运算时,要注
意什么?
① 不能漏乘:
即单项式要乘遍多项式
的每一项
② 去括号时注意符号的确定.
基本功训练:
(5a2- a+1).(-6a3)
a2(a+1) – a(2a2+a-1)
= - 30a5+4a4-6a3
= -a3+a
你能利用如下的长方形卡片拼成更大的长方形吗?
a
b
a
m
n
b
n
m
a
b
a
m
n
b
n
m
动手画一画
你能用不同的形式表示
所拼图的面积吗?
m
b
a
m
b
b
n
m
可以看成四个矩形的面积和:
可以看成一个大矩形的面积:
(a+n)(b+m)
(a+n)(b+m)=ab+am+nb+nm)
所以能得到等式:
多项式与多项式相乘:
(a+n)(b+m)=
ab
+ am
+ nb
+nm
如何进行多项式与多项式相乘的运算 ?
先用一个多项式的每一项
乘另一个多项式的每一项,
再把所得的积相加。
例1 计算:
①
②
③
④
①
②
③
④
①
②
③
④
注意事项:
1、多项式乘法中,每一项应连同符号相乘;切记“同号得正,异号得负”;
2、要防止漏乘;
例2 计算:
(3x-1)(x+3)
3、多项式相乘的积在没有合并同类项前,所得的项数是两个多项式项数的积;
4、乘积中,有同类项时一定要合并,得到最简结果。
=3x?x
+3x?3
-
1?x
-
1×3
= 3x2 + 8x –3
随堂练习
(1) (m+2n)(m?2n);
(2) (2n +5)(n?3) ;
计算:
(3) (x+2y)2 ;
合作探究
(x+3)(x-5)
(2)(x-3)(x+5)
(3)(x+3)(x+5)
(4)(x-3)(x-5)
请观察上面四题的特点,你能总结出它们结果的规律吗?
=x2-2x-15
=x2+2x-15
=x2+8x+15
=x2-8x+15
例2 计算:
规律:
+
×
练习:用推导的公式计算:
合作探究:
当a为何值时,(x2+ax+1)(x2-3x+2)的运算结果不含有x2项.
先利用多项式与多项式相乘的乘法法则进行计算,然后合并同类项,合并时含有x2的系数和为0即可。
本节课你的收获是什么?
运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.
最后的计算结果要化简 ̄ ̄ ̄
合并同类项.
如何进行多项式与多项式乘法运算?
在寻求真理的长征中,唯有学习,不断地学习,勤奋地学习,有创造地学习,才能越重山,跨峻岭。
——华罗庚
作业:
1.课本第29页练习计算
2.习题12.2第5.6题
