人教版九年级上册22.1.1二次函数概念课件(共27张PPT)
文档属性
| 名称 | 人教版九年级上册22.1.1二次函数概念课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览








文档简介
知识回顾
1.一元二次方程的一般形式是什么?
2。一次函数、正比例函数的定义是什么?
喷泉(1)
创设情境,导入新课
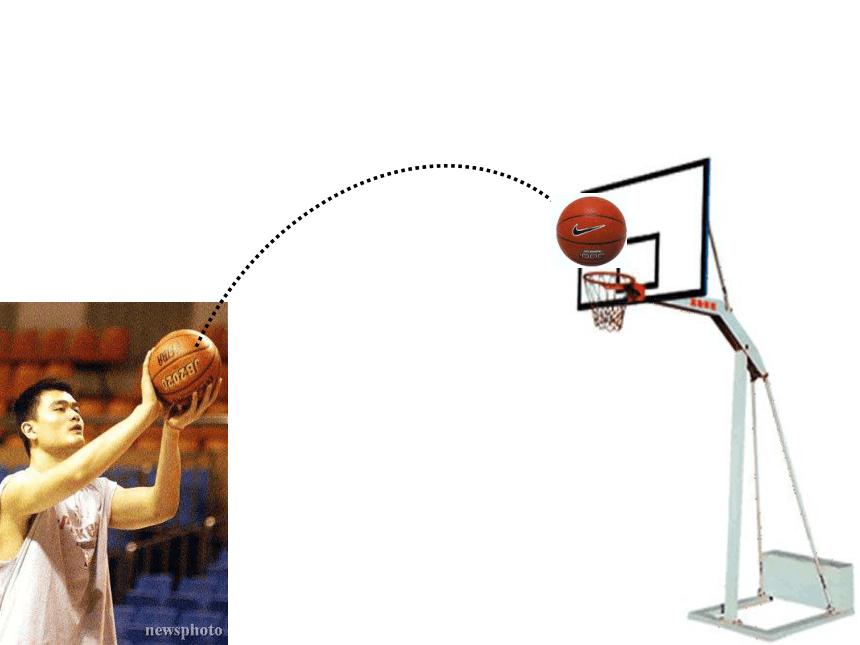
(2)你们知道:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
(1)你们喜欢打篮球吗?
问题:
二次函数
请用适当的函数解析式表示下列问题情境中的两个变量 y 与 x 之间的关系:
合作学习,探索新知 :
(1) 个球队参加比赛,每两队之间进行一场比赛,比赛的场数 与球队数 有什么关系?
(2)某种产品现在的年产量是20 ,计划今后两年增加产量。如果每年都比上一年的产量增加 倍,那么两年后这种产品的产量 将随计划所定的 的值而确定, 与 之间的关系应怎样表示?
1.
2.
上述两个问题中的函数解析式具有哪些共同的特征?
经化简后都具有y=ax?+bx+c 的形式.
(a,b,c是常数, )
a≠0
合作学习,探索新知 :
(1)关系式都是整式,(2)自变量的最高次数是二次,(3)二次项系数不等于零
我们把形如y=ax?+bx+c(其中a,b,c是常数,a≠0)的函数叫做二次函数
称:ax2叫做二次项,a为二次项系数
bx叫做一次项, b为一次项系数
c为常数项,
又例:y=x? + 2x – 3
做一做:
(1)正方形边长为x(cm),它的面积y(cm2)是多少?
(2)矩形的长是4厘米,宽是3厘米,如果将其长增加x厘米,宽增加2x厘米,则面积增加到y平方厘米,试写出y与x的关系式.
1.下列函数中,哪些是二次函数?
抓住机遇 展示自我
是
不是
是
不是
先化简后判断
2、下列函数中,哪些是二次函数?
( )
( )
( )
否
是
否
否
( )
是
( )
知识运用
3、下列函数中,哪些是二次函数?
(1)y=3x-1 (2)y=3x2
(3)y=3x3+2x2 (4)y=2x2-2x+1
(5)y=x-2+x (6)y=x2-x(1+x)
例1: 关于x的函数 是二次函数, 求m的值.
解: 由题意可得
注意:二次函数的二次项系数不能为零
驶向胜利的彼岸
练习m取何值时,函数是 y= (m+1)x
+(m-3)x+m 是二次函数?
知识运用
练习2、请举1个符合以下条件的y关于x的二次函数的例子
练一练:
(1)二次项系数是一次项系数的2倍, 常数项为任意值。
(2)二次项系数为-5,一次项系数为常数项的3倍。
展示才智
3、若函数 为二次函数,求m的值。
解:因为该函数为二次函数,
则
解(1)得:m=2或-1
解(2)得:
所以m=2
判断:下列函数是否为二次函数,如果是,指出其中常数a.b.c的值.
(1) y=1— (2)y=x(x-5)
(3)y= x2- x+1
(4) y=3x(2-x)+ 3x2
(5)y= (6) y=
(7)y= x4+2x2-1 (8)y=ax2+bx+c
例3:已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析试.
{
待定系数法
例4. 已知二次函数y=x?+px+q,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的解析式.
{
这节课你有什么收获和体会?
1.一元二次方程的一般形式是什么?
2。一次函数、正比例函数的定义是什么?
喷泉(1)
创设情境,导入新课
(2)你们知道:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?
(1)你们喜欢打篮球吗?
问题:
二次函数
请用适当的函数解析式表示下列问题情境中的两个变量 y 与 x 之间的关系:
合作学习,探索新知 :
(1) 个球队参加比赛,每两队之间进行一场比赛,比赛的场数 与球队数 有什么关系?
(2)某种产品现在的年产量是20 ,计划今后两年增加产量。如果每年都比上一年的产量增加 倍,那么两年后这种产品的产量 将随计划所定的 的值而确定, 与 之间的关系应怎样表示?
1.
2.
上述两个问题中的函数解析式具有哪些共同的特征?
经化简后都具有y=ax?+bx+c 的形式.
(a,b,c是常数, )
a≠0
合作学习,探索新知 :
(1)关系式都是整式,(2)自变量的最高次数是二次,(3)二次项系数不等于零
我们把形如y=ax?+bx+c(其中a,b,c是常数,a≠0)的函数叫做二次函数
称:ax2叫做二次项,a为二次项系数
bx叫做一次项, b为一次项系数
c为常数项,
又例:y=x? + 2x – 3
做一做:
(1)正方形边长为x(cm),它的面积y(cm2)是多少?
(2)矩形的长是4厘米,宽是3厘米,如果将其长增加x厘米,宽增加2x厘米,则面积增加到y平方厘米,试写出y与x的关系式.
1.下列函数中,哪些是二次函数?
抓住机遇 展示自我
是
不是
是
不是
先化简后判断
2、下列函数中,哪些是二次函数?
( )
( )
( )
否
是
否
否
( )
是
( )
知识运用
3、下列函数中,哪些是二次函数?
(1)y=3x-1 (2)y=3x2
(3)y=3x3+2x2 (4)y=2x2-2x+1
(5)y=x-2+x (6)y=x2-x(1+x)
例1: 关于x的函数 是二次函数, 求m的值.
解: 由题意可得
注意:二次函数的二次项系数不能为零
驶向胜利的彼岸
练习m取何值时,函数是 y= (m+1)x
+(m-3)x+m 是二次函数?
知识运用
练习2、请举1个符合以下条件的y关于x的二次函数的例子
练一练:
(1)二次项系数是一次项系数的2倍, 常数项为任意值。
(2)二次项系数为-5,一次项系数为常数项的3倍。
展示才智
3、若函数 为二次函数,求m的值。
解:因为该函数为二次函数,
则
解(1)得:m=2或-1
解(2)得:
所以m=2
判断:下列函数是否为二次函数,如果是,指出其中常数a.b.c的值.
(1) y=1— (2)y=x(x-5)
(3)y= x2- x+1
(4) y=3x(2-x)+ 3x2
(5)y= (6) y=
(7)y= x4+2x2-1 (8)y=ax2+bx+c
例3:已知关于x的二次函数,当x=-1时,函数值为10,当x=1时,函数值为4,当x=2时,函数值为7,求这个二次函数的解析试.
{
待定系数法
例4. 已知二次函数y=x?+px+q,当x=1时,函数值为4,当x=2时,函数值为- 5, 求这个二次函数的解析式.
{
这节课你有什么收获和体会?
同课章节目录
