人教版八年级上册数学11.1.1三角形的边课件(共19张PPT)
文档属性
| 名称 | 人教版八年级上册数学11.1.1三角形的边课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览



文档简介
11.1 与三角形有关的线段
11.1.1 三角形的边
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
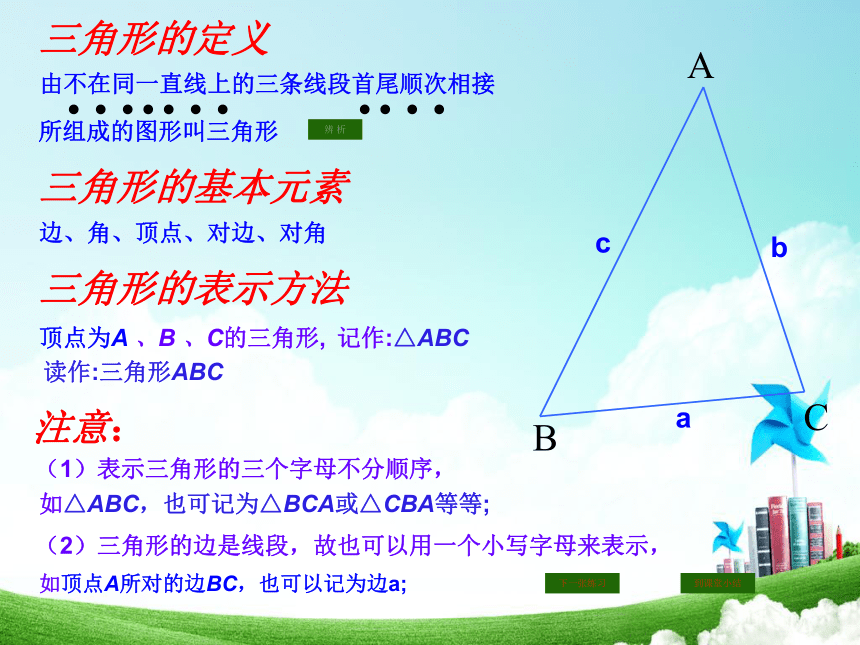
三角形的定义
三角形的表示方法
注意:
(1)表示三角形的三个字母不分顺序,
(2)三角形的边是线段,故也可以用一个小写字母来表示,
A
C
B
a
c
b
顶点为A 、B 、C的三角形,
读作:三角形ABC
下一张练习
到课堂小结
由不在同一直线上的三条线段首尾顺次相接
所组成的图形叫三角形
辨 析
三角形的基本元素
边、角、顶点、对边、对角
记作:△ABC
如△ABC,也可记为△BCA或△CBA等等;
如顶点A所对的边BC,也可以记为边a;
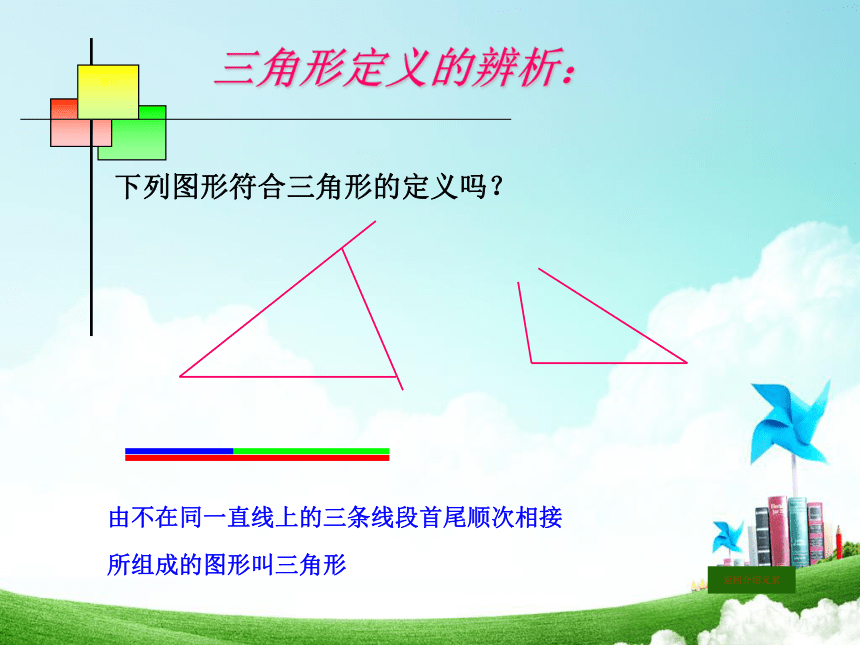
三角形定义的辨析:
下列图形符合三角形的定义吗?
返回介绍元素
由不在同一直线上的三条线段首尾顺次相接
所组成的图形叫三角形
蔡伟
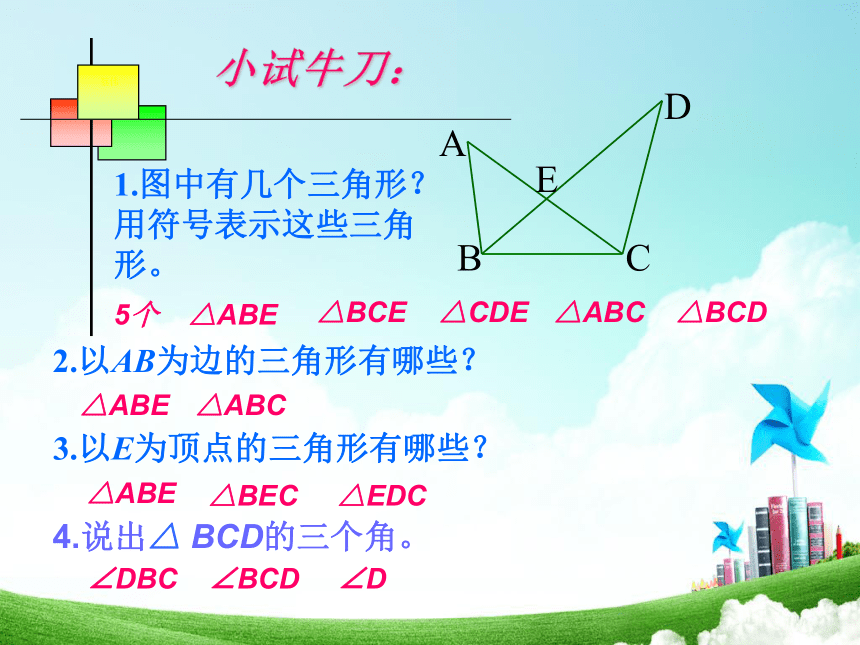
小试牛刀:
1.图中有几个三角形?用符号表示这些三角形。
A
D
C
B
E
5个
△ABE
△CDE
△BCE
△ABC
△BCD
2.以AB为边的三角形有哪些?
3.以E为顶点的三角形有哪些?
△ABE
△ABC
△ABE
△BEC
△EDC
4.说出△ BCD的三个角。
∠DBC
∠BCD
∠D
蔡伟
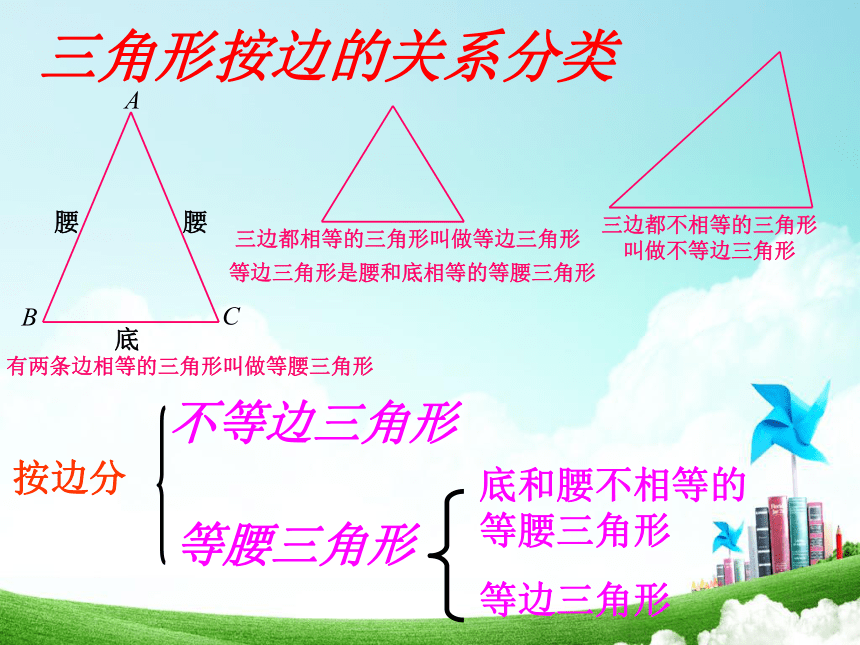
三角形按边的关系分类
有两条边相等的三角形叫做等腰三角形
三边都相等的三角形叫做等边三角形
等边三角形是腰和底相等的等腰三角形
三边都不相等的三角形
叫做不等边三角形
不等边三角形
等腰三角形
底和腰不相等的等腰三角形
等边三角形
按边分
锐角三角形
直角三角形
钝角三角形
三角形的分类
按角分
不等边三角形
等腰三角形
底和腰不相等的等腰三角形
等边三角形
按边分
到课堂小结
试一试:
判断:
(2)等边三角形是特殊的等腰三角形.( )
(1)不等边三角形就是有两边不相等的三角形.( )
√
×
(3)等腰三角形的腰和底一定不相等.( )
×
(4)等边三角形是锐角三角形.( )
(5)等腰直角三角形不是等腰三角形.( )
×
√
蔡伟
探究1:三角形三边的关系
AB+BC____AC
AB+AC____BC
BC+AC____AB
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?能证明你的结论吗?
三角形两边之和大于第三边?
用一用:你能一步迈出2.5m吗?
1.2m
1.2m
1.2m
地面
蔡伟
探究2:三条线段能够组成三角形的条件
请大家拿出信封中的小木棍将它们首尾顺次相接,你能摆出什么三角形?
×
√
×
较小两条线段之和小于第三条
较小两条线段之和等于第三条
较小两条线段之和大于第三条
三条线段能够组成三角形的条件:
较小两条线段之和大于第三条
到课堂小结
结论:
蔡伟
1.下列长度的三条线段能否组成三角形?为什么?
(1) 1,10,8 ( )
(2) 3,5,6 ( )
(3) 5,10,10 ( )
(4) 2,6,9 ( )
比一比:
不能
能
能
不能
2.已知等腰三角形的两边长分别为5cm和11cm,
则它的周长为____cm
27
5,5,11
11,11,5
√
×
到回顾反思
蔡伟
例题:
用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为4cm的等腰三角形吗?为什么?
例题:
用一条长为18cm的细绳围成一个等腰三角形.
(2)能围成有一边的长为4cm的等腰三角形吗?为什么?
到回顾反思
练一练:
2.已知等腰三角形的两边长分别为5cm和7cm,
则它的周长为_________cm.
5,5,7
7,7,5
17或19
√
√
到回顾反思
练一练:
到回顾反思
①7、5、3
②10、5、3
③10、7、3
④10、7、5
3.用一条长为20cm的细绳,能围成有一边
长为10cm的等腰三角形吗?为什么?
蔡伟
1、本节课你有哪些收获?
2、还有哪些地方不很清楚?
回顾反思
蔡伟
1、三角形定义、基本元素及表示方法;
2、三角形的分类;
课堂小结
4、三条线段能够组成三角形的条件;
3、三角形三边的关系;
蔡伟
谢谢!
11.1.1 三角形的边
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
三角形的定义
三角形的表示方法
注意:
(1)表示三角形的三个字母不分顺序,
(2)三角形的边是线段,故也可以用一个小写字母来表示,
A
C
B
a
c
b
顶点为A 、B 、C的三角形,
读作:三角形ABC
下一张练习
到课堂小结
由不在同一直线上的三条线段首尾顺次相接
所组成的图形叫三角形
辨 析
三角形的基本元素
边、角、顶点、对边、对角
记作:△ABC
如△ABC,也可记为△BCA或△CBA等等;
如顶点A所对的边BC,也可以记为边a;
三角形定义的辨析:
下列图形符合三角形的定义吗?
返回介绍元素
由不在同一直线上的三条线段首尾顺次相接
所组成的图形叫三角形
蔡伟
小试牛刀:
1.图中有几个三角形?用符号表示这些三角形。
A
D
C
B
E
5个
△ABE
△CDE
△BCE
△ABC
△BCD
2.以AB为边的三角形有哪些?
3.以E为顶点的三角形有哪些?
△ABE
△ABC
△ABE
△BEC
△EDC
4.说出△ BCD的三个角。
∠DBC
∠BCD
∠D
蔡伟
三角形按边的关系分类
有两条边相等的三角形叫做等腰三角形
三边都相等的三角形叫做等边三角形
等边三角形是腰和底相等的等腰三角形
三边都不相等的三角形
叫做不等边三角形
不等边三角形
等腰三角形
底和腰不相等的等腰三角形
等边三角形
按边分
锐角三角形
直角三角形
钝角三角形
三角形的分类
按角分
不等边三角形
等腰三角形
底和腰不相等的等腰三角形
等边三角形
按边分
到课堂小结
试一试:
判断:
(2)等边三角形是特殊的等腰三角形.( )
(1)不等边三角形就是有两边不相等的三角形.( )
√
×
(3)等腰三角形的腰和底一定不相等.( )
×
(4)等边三角形是锐角三角形.( )
(5)等腰直角三角形不是等腰三角形.( )
×
√
蔡伟
探究1:三角形三边的关系
AB+BC____AC
AB+AC____BC
BC+AC____AB
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?能证明你的结论吗?
三角形两边之和大于第三边?
用一用:你能一步迈出2.5m吗?
1.2m
1.2m
1.2m
地面
蔡伟
探究2:三条线段能够组成三角形的条件
请大家拿出信封中的小木棍将它们首尾顺次相接,你能摆出什么三角形?
×
√
×
较小两条线段之和小于第三条
较小两条线段之和等于第三条
较小两条线段之和大于第三条
三条线段能够组成三角形的条件:
较小两条线段之和大于第三条
到课堂小结
结论:
蔡伟
1.下列长度的三条线段能否组成三角形?为什么?
(1) 1,10,8 ( )
(2) 3,5,6 ( )
(3) 5,10,10 ( )
(4) 2,6,9 ( )
比一比:
不能
能
能
不能
2.已知等腰三角形的两边长分别为5cm和11cm,
则它的周长为____cm
27
5,5,11
11,11,5
√
×
到回顾反思
蔡伟
例题:
用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边的长为4cm的等腰三角形吗?为什么?
例题:
用一条长为18cm的细绳围成一个等腰三角形.
(2)能围成有一边的长为4cm的等腰三角形吗?为什么?
到回顾反思
练一练:
2.已知等腰三角形的两边长分别为5cm和7cm,
则它的周长为_________cm.
5,5,7
7,7,5
17或19
√
√
到回顾反思
练一练:
到回顾反思
①7、5、3
②10、5、3
③10、7、3
④10、7、5
3.用一条长为20cm的细绳,能围成有一边
长为10cm的等腰三角形吗?为什么?
蔡伟
1、本节课你有哪些收获?
2、还有哪些地方不很清楚?
回顾反思
蔡伟
1、三角形定义、基本元素及表示方法;
2、三角形的分类;
课堂小结
4、三条线段能够组成三角形的条件;
3、三角形三边的关系;
蔡伟
谢谢!
