人教版数学八年级上册13.3.1等腰三角形的判定课件 (15张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.3.1等腰三角形的判定课件 (15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 19:55:04 | ||
图片预览

文档简介
等腰三角形的判定
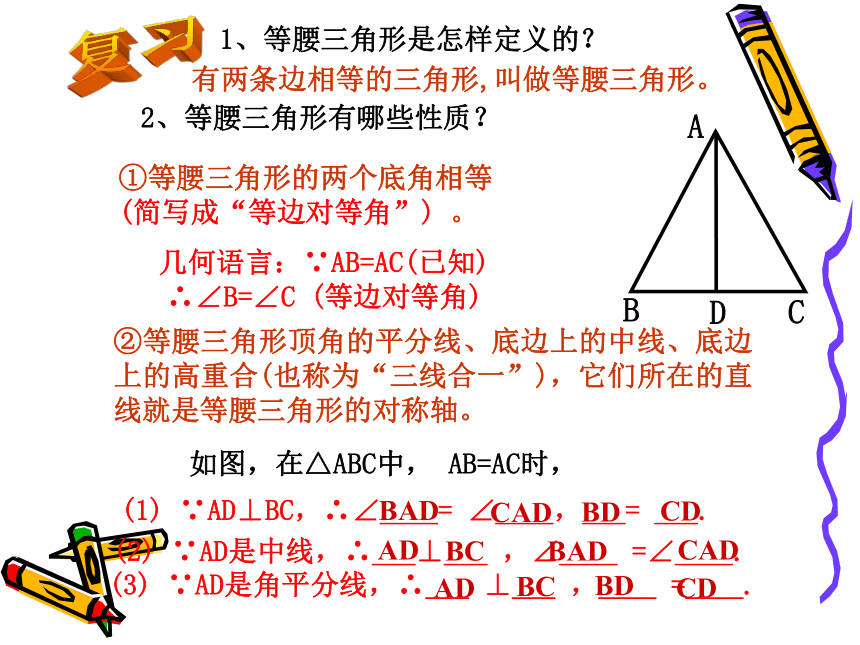
1、等腰三角形是怎样定义的?
有两条边相等的三角形,叫做等腰三角形。
②等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”),它们所在的直线就是等腰三角形的对称轴。
①等腰三角形的两个底角相等
(简写成“等边对等角”) 。
2、等腰三角形有哪些性质?
D
A
B
C
如图,在△ABC中, AB=AC时,
(1) ∵AD⊥BC,∴∠____= ∠____,___= ___.
(2) ∵AD是中线,∴___⊥___ ,∠____ =∠____.
(3) ∵AD是角平分线,∴___ ⊥___ ,____ =____.
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
几何语言:∵AB=AC(已知) ∴∠B=∠C (等边对等角)
A
B
O
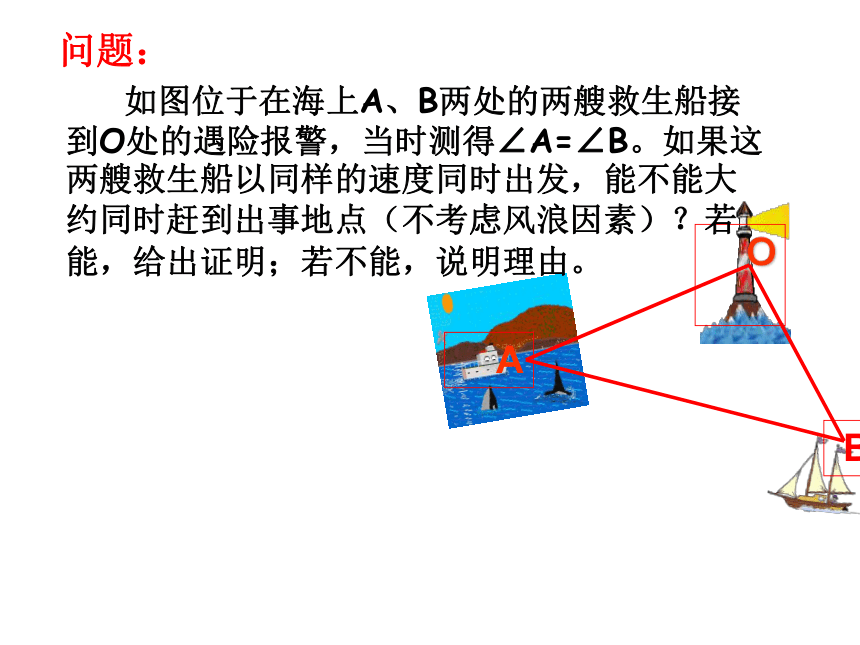
问题:
如图位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?若能,给出证明;若不能,说明理由。
A
B
O
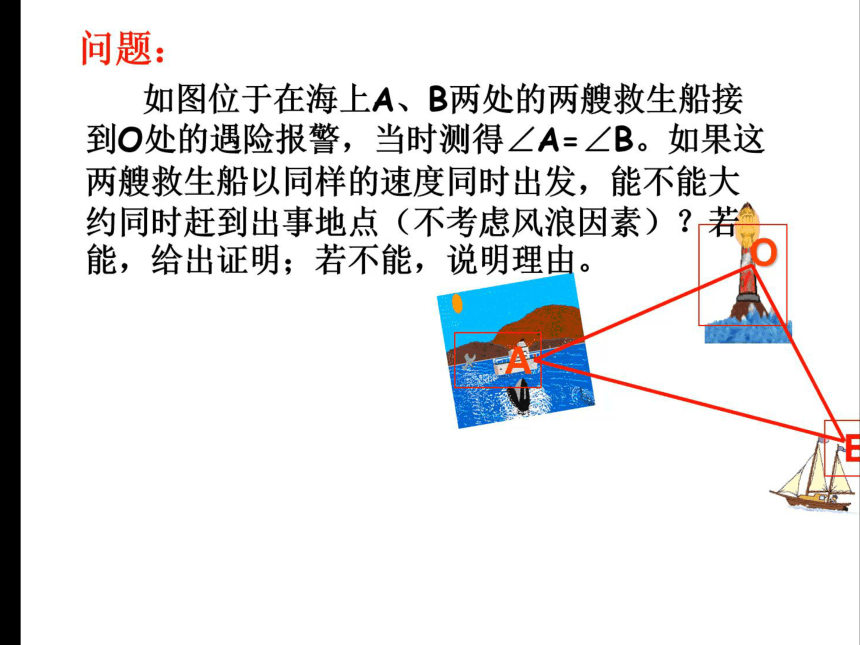
问题:
如图位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?若能,给出证明;若不能,说明理由。
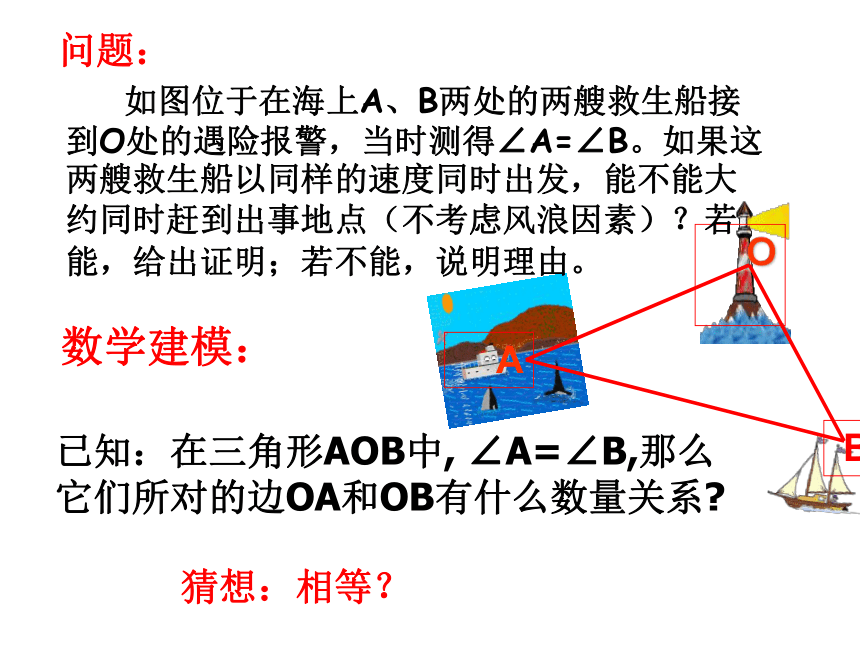
已知:在三角形AOB中, ∠A=∠B,那么它们所对的边OA和OB有什么数量关系?
猜想:相等?
数学建模:
A
B
O
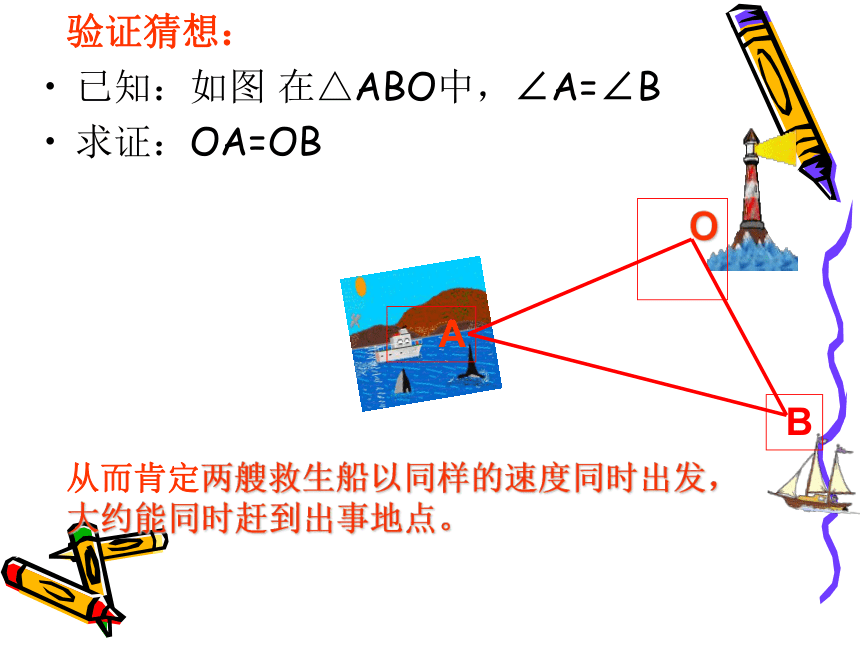
验证猜想:
已知:如图 在△ABO中,∠A=∠B
求证:OA=OB
从而肯定两艘救生船以同样的速度同时出发,
大约能同时赶到出事地点。
例2、求证:如果三角形一个外角的平分线
平行于三角形的一边,那么这个三角形是等
腰三角形。
A
E
C
B
D
已知:AE是△ ABC的外角平分线,
且AE ∥ BC.
求证:AB=AC
A
E
C
B
D
求证:AB=AC
已知:AE是△ ABC的外角平分线,
且AE ∥ BC.
平行+平分
等腰三角形
1.如图,∠A=36°,∠DBC=36°,∠C=72°.
分别计算∠1= ,∠2= ,图中的
等腰三角形分别 .
A
B
C
D
1
2
72°
36°
△ ABC、△ ABD、△BCD
。
2、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?
3、如图,AC和BD相交于点O,且AB∥DC,OA=OB。
求证:OC=OD。
A
B
C
D
E
F
已知:在△ ABC中,AB=AC, ∠ABC和∠ACB
平分线交于点D.求:
(1)写出图中的等腰三角形?并证明
(2)过点D作EF∥BC,写出图中的等腰三角形,并证明
(3)直接写出EF,BE,CF的数量关系
(4)若AB≠AC,以上结论还成立吗?为什么?
小结
通过这节课的学习,你有哪些收获?
1、等腰三角形的判定方法:
定义、判定定理
2、等腰三角形的判定及其在实际生活中的应用
作业
必做:能力培养第二课时
选作:能培p57——10
1、等腰三角形是怎样定义的?
有两条边相等的三角形,叫做等腰三角形。
②等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”),它们所在的直线就是等腰三角形的对称轴。
①等腰三角形的两个底角相等
(简写成“等边对等角”) 。
2、等腰三角形有哪些性质?
D
A
B
C
如图,在△ABC中, AB=AC时,
(1) ∵AD⊥BC,∴∠____= ∠____,___= ___.
(2) ∵AD是中线,∴___⊥___ ,∠____ =∠____.
(3) ∵AD是角平分线,∴___ ⊥___ ,____ =____.
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
几何语言:∵AB=AC(已知) ∴∠B=∠C (等边对等角)
A
B
O
问题:
如图位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?若能,给出证明;若不能,说明理由。
A
B
O
问题:
如图位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?若能,给出证明;若不能,说明理由。
已知:在三角形AOB中, ∠A=∠B,那么它们所对的边OA和OB有什么数量关系?
猜想:相等?
数学建模:
A
B
O
验证猜想:
已知:如图 在△ABO中,∠A=∠B
求证:OA=OB
从而肯定两艘救生船以同样的速度同时出发,
大约能同时赶到出事地点。
例2、求证:如果三角形一个外角的平分线
平行于三角形的一边,那么这个三角形是等
腰三角形。
A
E
C
B
D
已知:AE是△ ABC的外角平分线,
且AE ∥ BC.
求证:AB=AC
A
E
C
B
D
求证:AB=AC
已知:AE是△ ABC的外角平分线,
且AE ∥ BC.
平行+平分
等腰三角形
1.如图,∠A=36°,∠DBC=36°,∠C=72°.
分别计算∠1= ,∠2= ,图中的
等腰三角形分别 .
A
B
C
D
1
2
72°
36°
△ ABC、△ ABD、△BCD
。
2、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?
3、如图,AC和BD相交于点O,且AB∥DC,OA=OB。
求证:OC=OD。
A
B
C
D
E
F
已知:在△ ABC中,AB=AC, ∠ABC和∠ACB
平分线交于点D.求:
(1)写出图中的等腰三角形?并证明
(2)过点D作EF∥BC,写出图中的等腰三角形,并证明
(3)直接写出EF,BE,CF的数量关系
(4)若AB≠AC,以上结论还成立吗?为什么?
小结
通过这节课的学习,你有哪些收获?
1、等腰三角形的判定方法:
定义、判定定理
2、等腰三角形的判定及其在实际生活中的应用
作业
必做:能力培养第二课时
选作:能培p57——10
