人教版数学八年级上册13.3.1探究等腰三角形的性质课件 (25张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.3.1探究等腰三角形的性质课件 (25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 19:55:09 | ||
图片预览





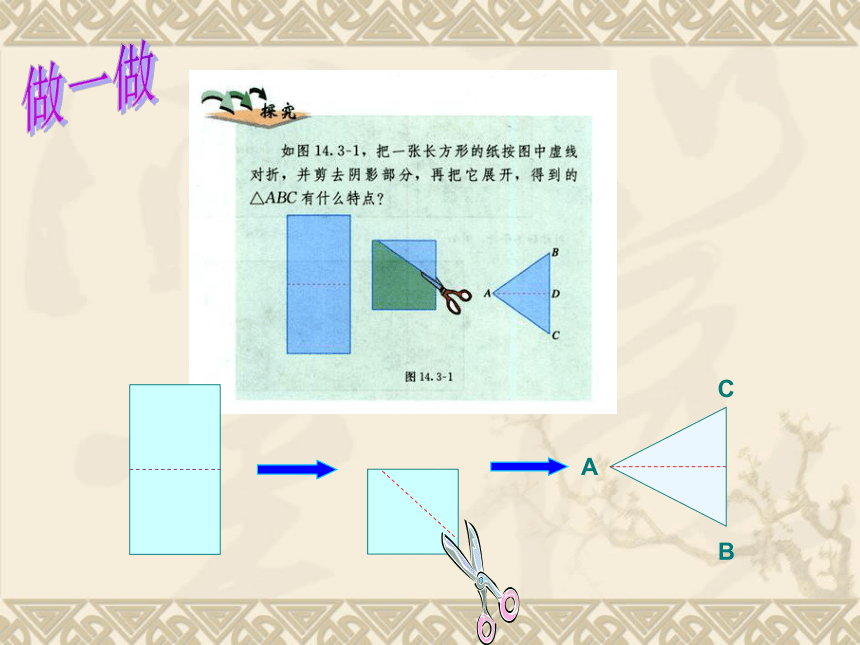
文档简介
等腰三角形
A
B
C
建筑工人在盖房子时,用一块等
腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底
边中点,就说
房梁是水平的,
你知道为什么
吗?
襄城县斌英中学 马晓丹
? 三维目标
知识与技能:理解等腰三角形的性质,会利用等腰三角形的性质,进行简单的推理、计算。
过程与方法:从设置问题?模型演示?自己动手探究发现等腰三角形的性质,培养学生的观察力、推理能力。
情感态度与价值观:引导学生对图形的观察、发现,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心。
?解读目标
A
C
B
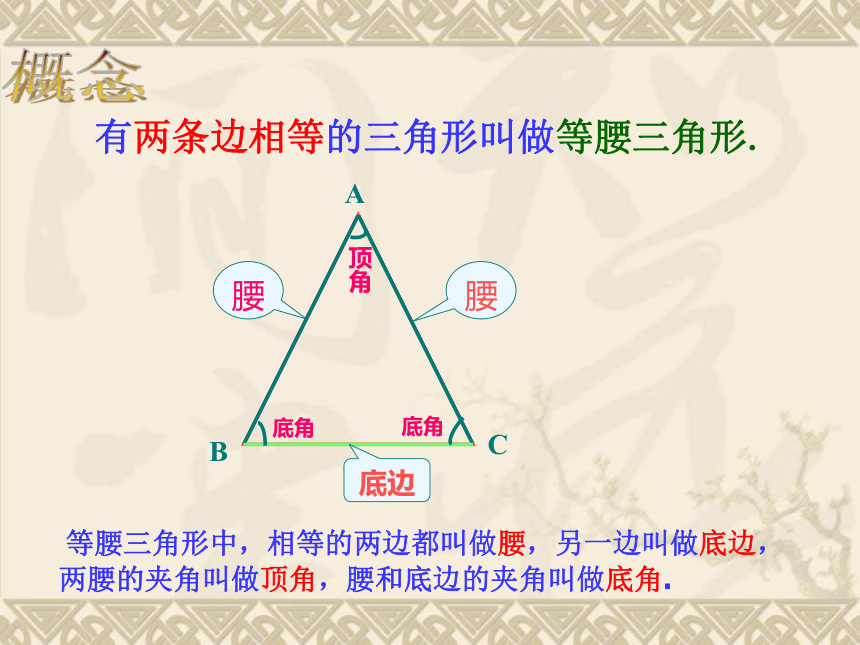
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
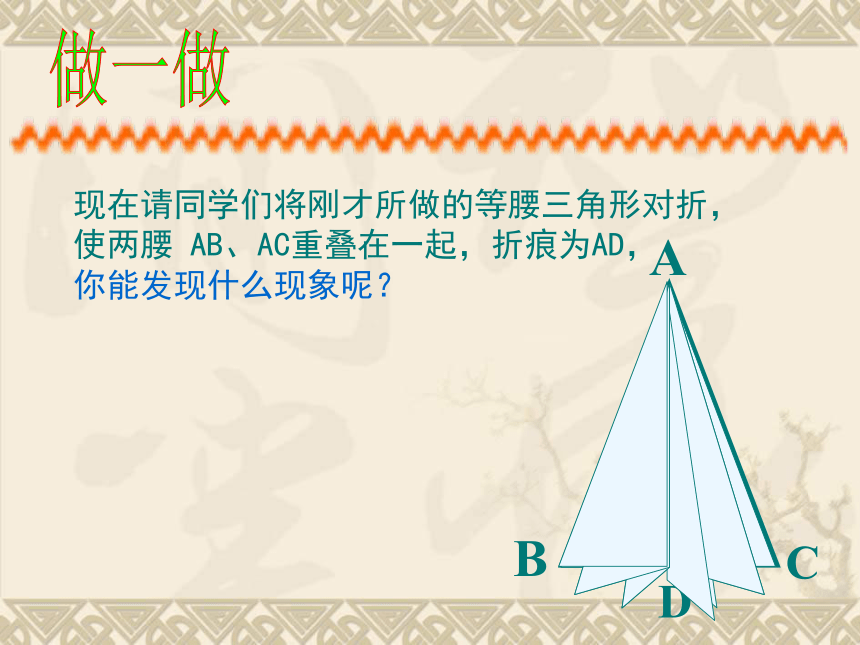
现在请同学们将刚才所做的等腰三角形对折,
使两腰 AB、AC重叠在一起,折痕为AD,
你能发现什么现象呢?
D
A
B
C
A
C
B
D
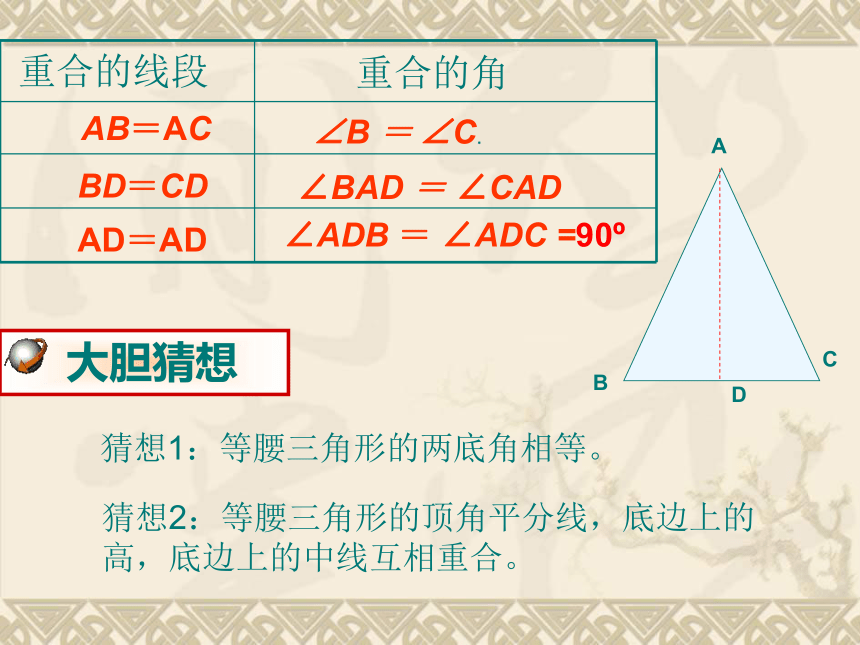
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC =90?
大胆猜想
猜想1:等腰三角形的两底角相等。
猜想2:等腰三角形的顶角平分线,底边上的高,底边上的中线互相重合。
重合的线段
重合的角
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
展示内容
展示
小组
点评小组
特别提示:
方法A
2组
1组
点评同学要声音洪亮,先点评板书,再点评思路,最后点评规律、方法。
(注意用双色笔)
非展示同学要认真整理、思考落实
非点评同学认真倾听,辨别对错,做好思考,准备质疑
方法B
4组
3组
方法C
6组
5组
展示点评任务分工及要求
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
A
B
C
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 ∠ADB=∠ADC =90?
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
性质1 : 等腰三角形的两个底角相等
(简称“等边对等角”,前提是在同一个三角形中。)
性质2 : 等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。
(简称“三线合一”,前提是三线合一在同一个等腰三角形中。)
∵AD⊥BC,
∴∠_____ = ∠_____,____= ____.
(2)∵AD是中线,
∴____⊥____ ,∠_____ =∠_____.
(3)∵AD是角平分线,
∴____ ⊥____ ,_____ =_____.
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
根据等腰三角形性质定理的证明,
在△ABC中, AB=AC时,
建筑工人在盖房子时,用一块等
腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底
边中点,就说
房梁是水平的,
你知道为什么
吗?
例1 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
A
B
C
D
注意方程思想的运用
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、
和底边上的高互相重合,
简称“三线合 一”
⒈等腰三角形一个底角为70°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个 角为______ __。
70°, 40°
70°,40°或55°,55°
35°,35°
小试牛刀
已知:如图, △ ABC中, ∠ABC=50 ?, ∠ACB=80 ?,延长
CB至D,使BD=BA,延长BC至E,使CE=CA .连结AD、AE.
求∠D、∠E、∠DAE的度数 .
A
B
C
D
E
谈谈你的收获!
1、必做题。P51 2, 3
2、选做题。根据工人师傅利用等腰
三角形检测房梁是否水平?
设计一道几何证明题并证明。
A
B
C
建筑工人在盖房子时,用一块等
腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底
边中点,就说
房梁是水平的,
你知道为什么
吗?
襄城县斌英中学 马晓丹
? 三维目标
知识与技能:理解等腰三角形的性质,会利用等腰三角形的性质,进行简单的推理、计算。
过程与方法:从设置问题?模型演示?自己动手探究发现等腰三角形的性质,培养学生的观察力、推理能力。
情感态度与价值观:引导学生对图形的观察、发现,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心。
?解读目标
A
C
B
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
现在请同学们将刚才所做的等腰三角形对折,
使两腰 AB、AC重叠在一起,折痕为AD,
你能发现什么现象呢?
D
A
B
C
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC =90?
大胆猜想
猜想1:等腰三角形的两底角相等。
猜想2:等腰三角形的顶角平分线,底边上的高,底边上的中线互相重合。
重合的线段
重合的角
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
展示内容
展示
小组
点评小组
特别提示:
方法A
2组
1组
点评同学要声音洪亮,先点评板书,再点评思路,最后点评规律、方法。
(注意用双色笔)
非展示同学要认真整理、思考落实
非点评同学认真倾听,辨别对错,做好思考,准备质疑
方法B
4组
3组
方法C
6组
5组
展示点评任务分工及要求
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
A
B
C
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 BD=CD
D
在△ABD和△ACD中
证明: 作△ABC 的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
A
B
C
则有 ∠ADB=∠ADC =90?
D
在Rt△ABD和Rt△ACD中
证明: 作△ABC 的高线AD
AB=AC
AD=AD
(公共边)
∴ Rt△ABD≌Rt△ACD
(HL)
∴ ∠B=∠C
(全等三角形对应角相等)
性质1 : 等腰三角形的两个底角相等
(简称“等边对等角”,前提是在同一个三角形中。)
性质2 : 等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。
(简称“三线合一”,前提是三线合一在同一个等腰三角形中。)
∵AD⊥BC,
∴∠_____ = ∠_____,____= ____.
(2)∵AD是中线,
∴____⊥____ ,∠_____ =∠_____.
(3)∵AD是角平分线,
∴____ ⊥____ ,_____ =_____.
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
根据等腰三角形性质定理的证明,
在△ABC中, AB=AC时,
建筑工人在盖房子时,用一块等
腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底
边中点,就说
房梁是水平的,
你知道为什么
吗?
例1 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
A
B
C
D
注意方程思想的运用
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、
和底边上的高互相重合,
简称“三线合 一”
⒈等腰三角形一个底角为70°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个 角为______ __。
70°, 40°
70°,40°或55°,55°
35°,35°
小试牛刀
已知:如图, △ ABC中, ∠ABC=50 ?, ∠ACB=80 ?,延长
CB至D,使BD=BA,延长BC至E,使CE=CA .连结AD、AE.
求∠D、∠E、∠DAE的度数 .
A
B
C
D
E
谈谈你的收获!
1、必做题。P51 2, 3
2、选做题。根据工人师傅利用等腰
三角形检测房梁是否水平?
设计一道几何证明题并证明。
