人教版数学九年级上册 23.1 图形的旋转 配套课件(共20张PPT)
文档属性
| 名称 | 人教版数学九年级上册 23.1 图形的旋转 配套课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-13 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
继“轴对称”和“平移”这两种图形变
换之后,我们今天要一起来学习
第三种图形变换:
同学们能举出一些现实生活中旋转的例子吗?
刮水器
转动的车轮
转动的时针
荡秋千
这些运动有什么共同的特征?
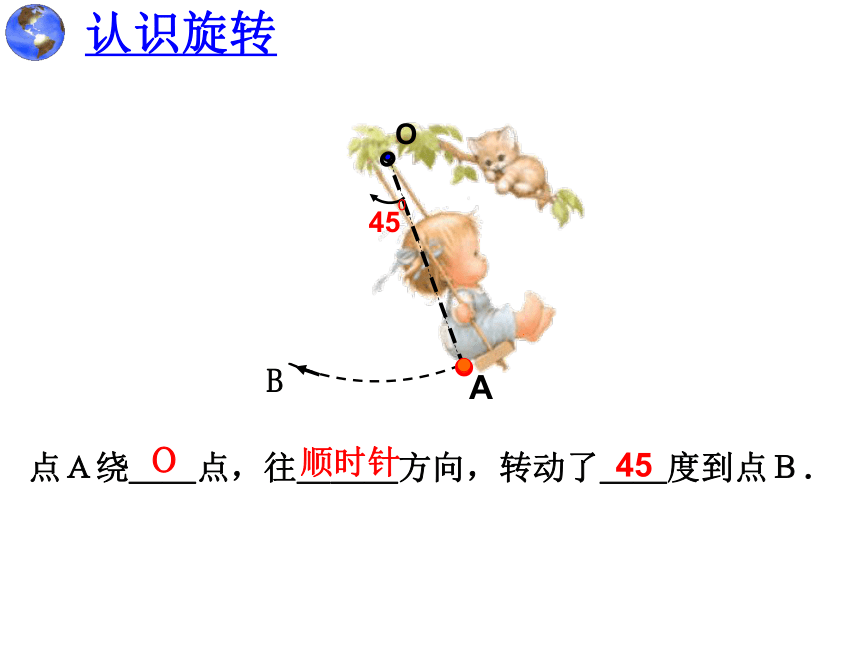
B
O
A
45
0
点A绕__点,往___方向,转动了__度到点B.
O
顺时针
45
认识旋转
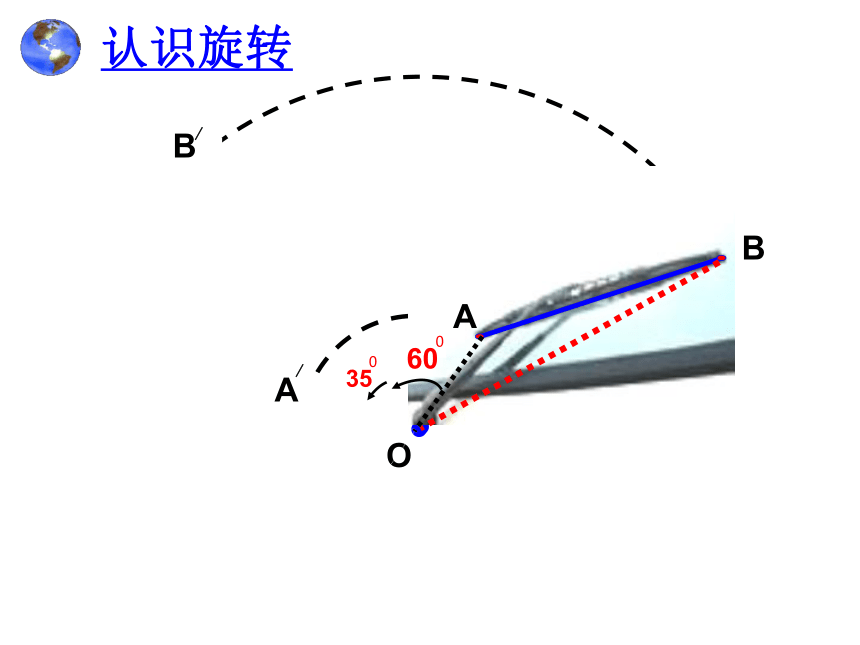
认识旋转
O
B
A
B
/
A
/
60
0
35
0
B
A
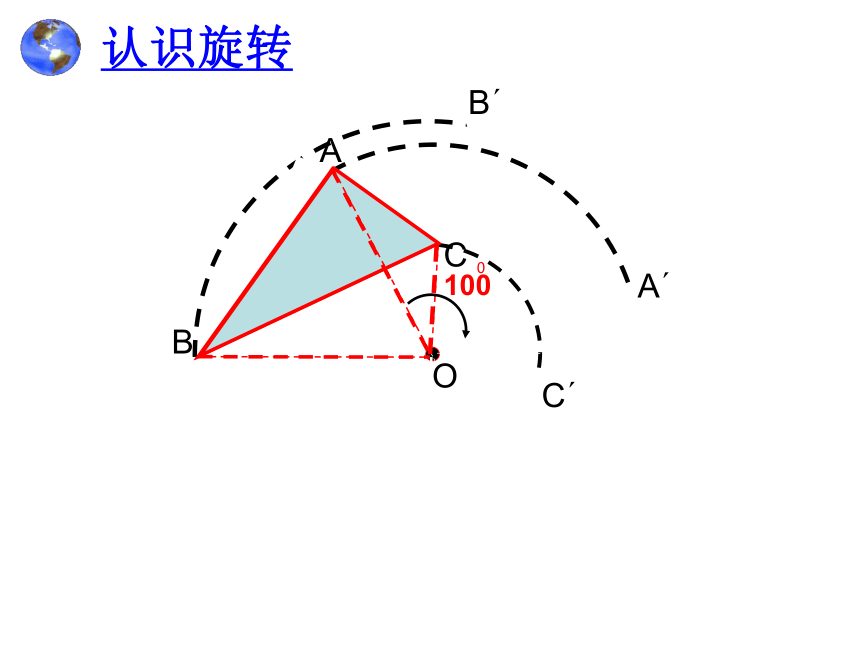
认识旋转
B
A
C
C
O
100
0
O
B
A
B
/
A
/
B
A
B
A
C
C
O
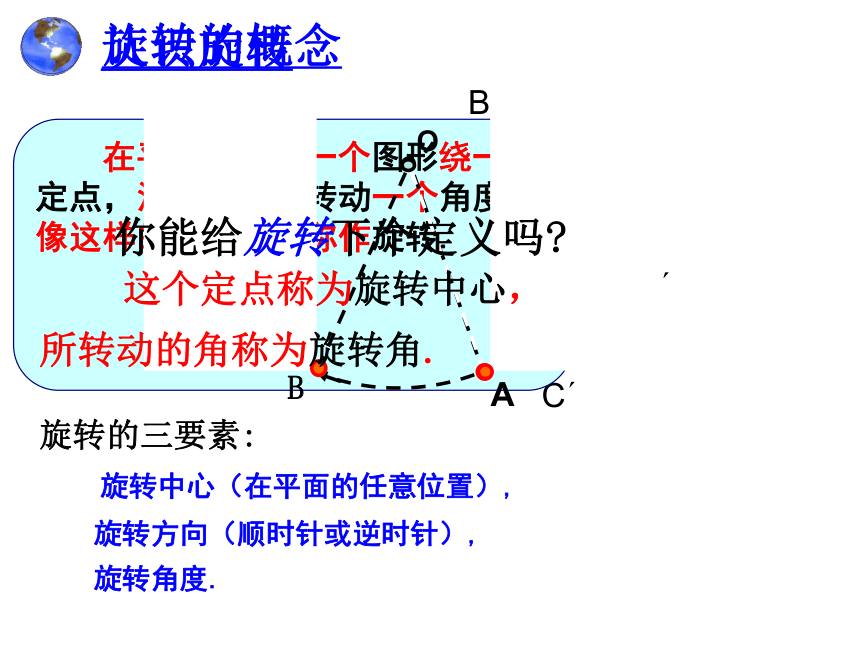
在平面内,把一个图形绕一个定点,沿某个方向转动一个角度,像这样的图形变换称作旋转.
B
O
A
认识旋转
这个定点称为旋转中心,
旋转的概念
旋转的三要素:
旋转中心(在平面的任意位置),
旋转方向(顺时针或逆时针),
旋转角度.
所转动的角称为旋转角.
你能给旋转下个定义吗
B
A
B
A
C
C
O
找一找
请仔细观察此图,
点A,线段AB,∠ABC分
别转到了什么位置?
点A
点A
线段A
B
∠ B
A
C
线段AB
∠ABC
对应点
对应线段
对应角
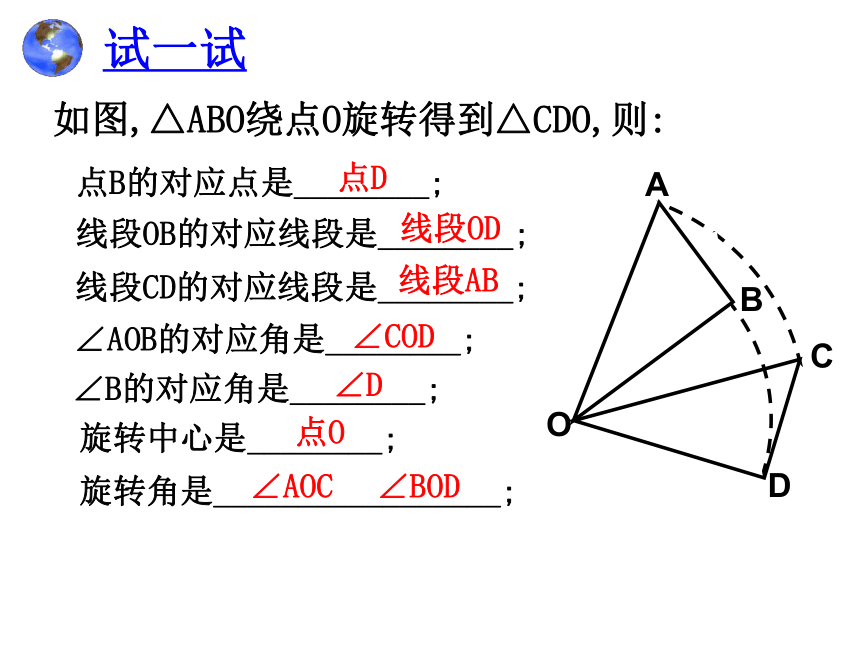
试一试
A
B
O
C
D
点B的对应点是________;
线段OB的对应线段是________;
线段CD的对应线段是________;
∠AOB的对应角是________;
∠B的对应角是________;
旋转中心是________;
旋转角是_________________;
如图,△ABO绕点O旋转得到△CDO,则:
点D
线段OD
线段AB
∠COD
∠D
点O
∠AOC
∠BOD
D
E
A
B
F
C
O
问题:
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心连线段的夹角等于旋转角.
旋转的性质:
1.在图形的旋转过程中,哪些发生了改变 哪些没有发生
改变
2.分别连结对应点A、D与旋转中心O,量一量线段OA与
线段OD,它们有什么关系 任意找一对对应点,量一下
它们与旋转中心的连线段,你能发现什么规律
3.量一下∠AOD的度数,再任意找几对对应点,分别量
一下对应点与旋转中心连线段的度数,你又能发现
什么规律?
◆旋转前、后的图形全等.
◆对应点到旋转中心的距离相等.
◆每一对对应点与旋转中心的连线所成的角彼此相等.
旋转的基本性质
◆图形的旋转是由旋转中心、旋转的角度和旋转方向决定.
例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
解:(1)它的旋转中心是钟表的轴心;
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为
(1)旋转中心是哪一点
(2)旋转角是多少度
例2.如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
A
B
F
C
E
G.
D
. H
(3)∠EAF等于多少度
(4)经过旋转,点B与点E分别移动到
什么位置
(5)若点G是线段BE的中点,经过旋转
后,点G移到了什么位置 请在图形
上作出.
(6)连结EF,请判断△AEF的形状,并说明理由.
(7)试判断四边形ABCD与AFCE面积的大小关系.
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
随堂练习
2. 下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
B
C
3.如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图
形所在的平面上可以作为旋转中心的点共有______个.
3个
●
F
A
B
D
E
C
4.已知,如图边长为1的正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,求图中阴影部分的面积.
4.已知,如图边长为1的正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,求图中阴影部分的面积.
6、如图,△ABC中,∠BAC=120°,以BC为边向外作等边三角形△BCD,把△ABD绕点D按顺时针方向旋转60°后到△ECD的位置,若AB=3,AC=2。求:∠BAD的度数和AD的长。
这节课你学到了什么知识?
你是用什么方法获得这些知识的?
本节课你还有什么地方没有解决吗?
旋转的定义:在平面内,将一个图形绕一个定点沿着某个方向转动一定的角度,这样的图形运动称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.
旋转的性质:
旋转前、后的图形全等;
旋转前后两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,旋转角相等;
对应点到旋转中心的距离相等.
继“轴对称”和“平移”这两种图形变
换之后,我们今天要一起来学习
第三种图形变换:
同学们能举出一些现实生活中旋转的例子吗?
刮水器
转动的车轮
转动的时针
荡秋千
这些运动有什么共同的特征?
B
O
A
45
0
点A绕__点,往___方向,转动了__度到点B.
O
顺时针
45
认识旋转
认识旋转
O
B
A
B
/
A
/
60
0
35
0
B
A
认识旋转
B
A
C
C
O
100
0
O
B
A
B
/
A
/
B
A
B
A
C
C
O
在平面内,把一个图形绕一个定点,沿某个方向转动一个角度,像这样的图形变换称作旋转.
B
O
A
认识旋转
这个定点称为旋转中心,
旋转的概念
旋转的三要素:
旋转中心(在平面的任意位置),
旋转方向(顺时针或逆时针),
旋转角度.
所转动的角称为旋转角.
你能给旋转下个定义吗
B
A
B
A
C
C
O
找一找
请仔细观察此图,
点A,线段AB,∠ABC分
别转到了什么位置?
点A
点A
线段A
B
∠ B
A
C
线段AB
∠ABC
对应点
对应线段
对应角
试一试
A
B
O
C
D
点B的对应点是________;
线段OB的对应线段是________;
线段CD的对应线段是________;
∠AOB的对应角是________;
∠B的对应角是________;
旋转中心是________;
旋转角是_________________;
如图,△ABO绕点O旋转得到△CDO,则:
点D
线段OD
线段AB
∠COD
∠D
点O
∠AOC
∠BOD
D
E
A
B
F
C
O
问题:
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心连线段的夹角等于旋转角.
旋转的性质:
1.在图形的旋转过程中,哪些发生了改变 哪些没有发生
改变
2.分别连结对应点A、D与旋转中心O,量一量线段OA与
线段OD,它们有什么关系 任意找一对对应点,量一下
它们与旋转中心的连线段,你能发现什么规律
3.量一下∠AOD的度数,再任意找几对对应点,分别量
一下对应点与旋转中心连线段的度数,你又能发现
什么规律?
◆旋转前、后的图形全等.
◆对应点到旋转中心的距离相等.
◆每一对对应点与旋转中心的连线所成的角彼此相等.
旋转的基本性质
◆图形的旋转是由旋转中心、旋转的角度和旋转方向决定.
例1:钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
解:(1)它的旋转中心是钟表的轴心;
(2)分针匀速旋转一周需要60
分,因此旋转20分,分针
旋转的角度为
(1)旋转中心是哪一点
(2)旋转角是多少度
例2.如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
A
B
F
C
E
G.
D
. H
(3)∠EAF等于多少度
(4)经过旋转,点B与点E分别移动到
什么位置
(5)若点G是线段BE的中点,经过旋转
后,点G移到了什么位置 请在图形
上作出.
(6)连结EF,请判断△AEF的形状,并说明理由.
(7)试判断四边形ABCD与AFCE面积的大小关系.
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
随堂练习
2. 下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
B
C
3.如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图
形所在的平面上可以作为旋转中心的点共有______个.
3个
●
F
A
B
D
E
C
4.已知,如图边长为1的正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,求图中阴影部分的面积.
4.已知,如图边长为1的正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,求图中阴影部分的面积.
6、如图,△ABC中,∠BAC=120°,以BC为边向外作等边三角形△BCD,把△ABD绕点D按顺时针方向旋转60°后到△ECD的位置,若AB=3,AC=2。求:∠BAD的度数和AD的长。
这节课你学到了什么知识?
你是用什么方法获得这些知识的?
本节课你还有什么地方没有解决吗?
旋转的定义:在平面内,将一个图形绕一个定点沿着某个方向转动一定的角度,这样的图形运动称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.
旋转的性质:
旋转前、后的图形全等;
旋转前后两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,旋转角相等;
对应点到旋转中心的距离相等.
同课章节目录
